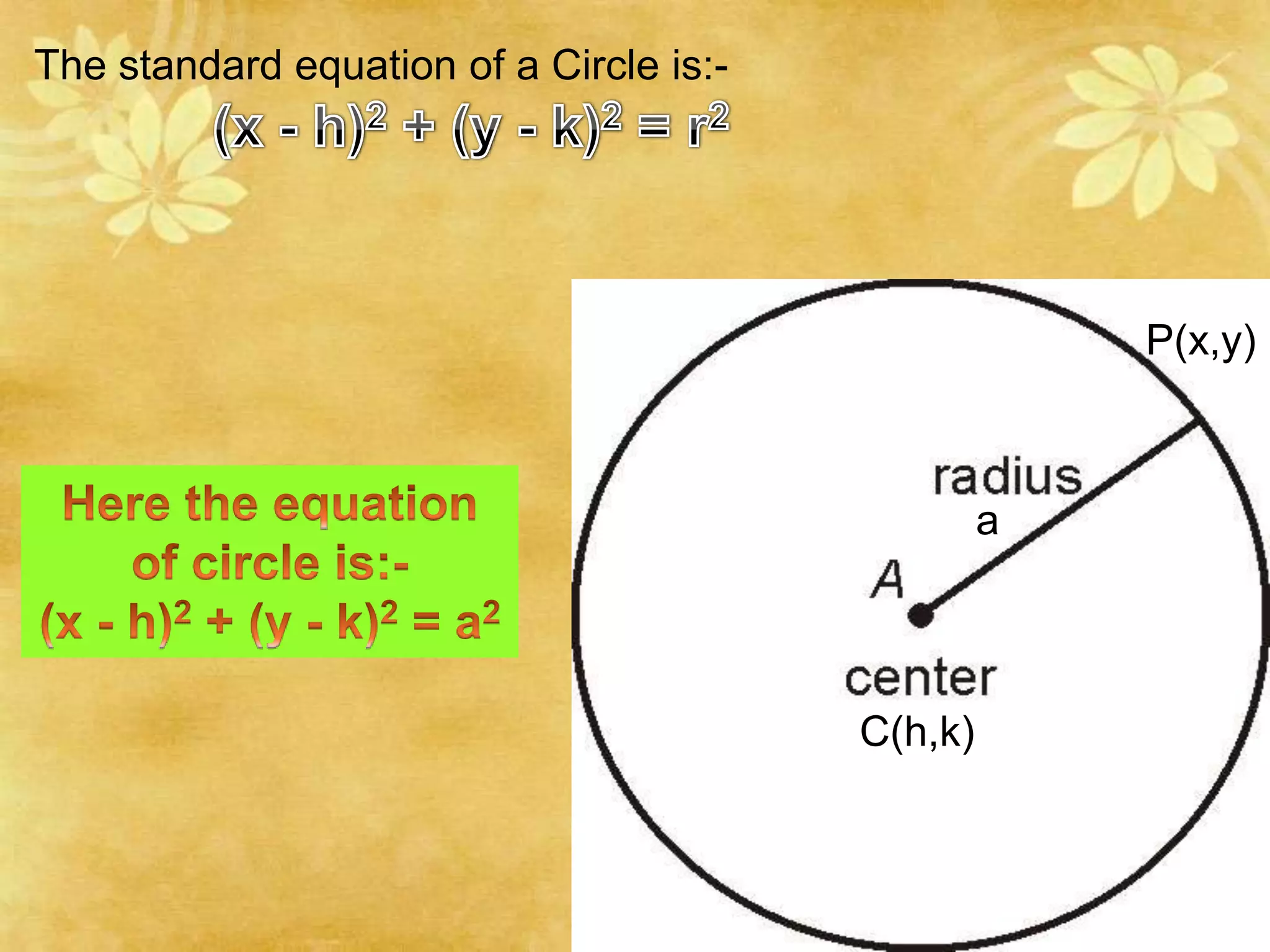
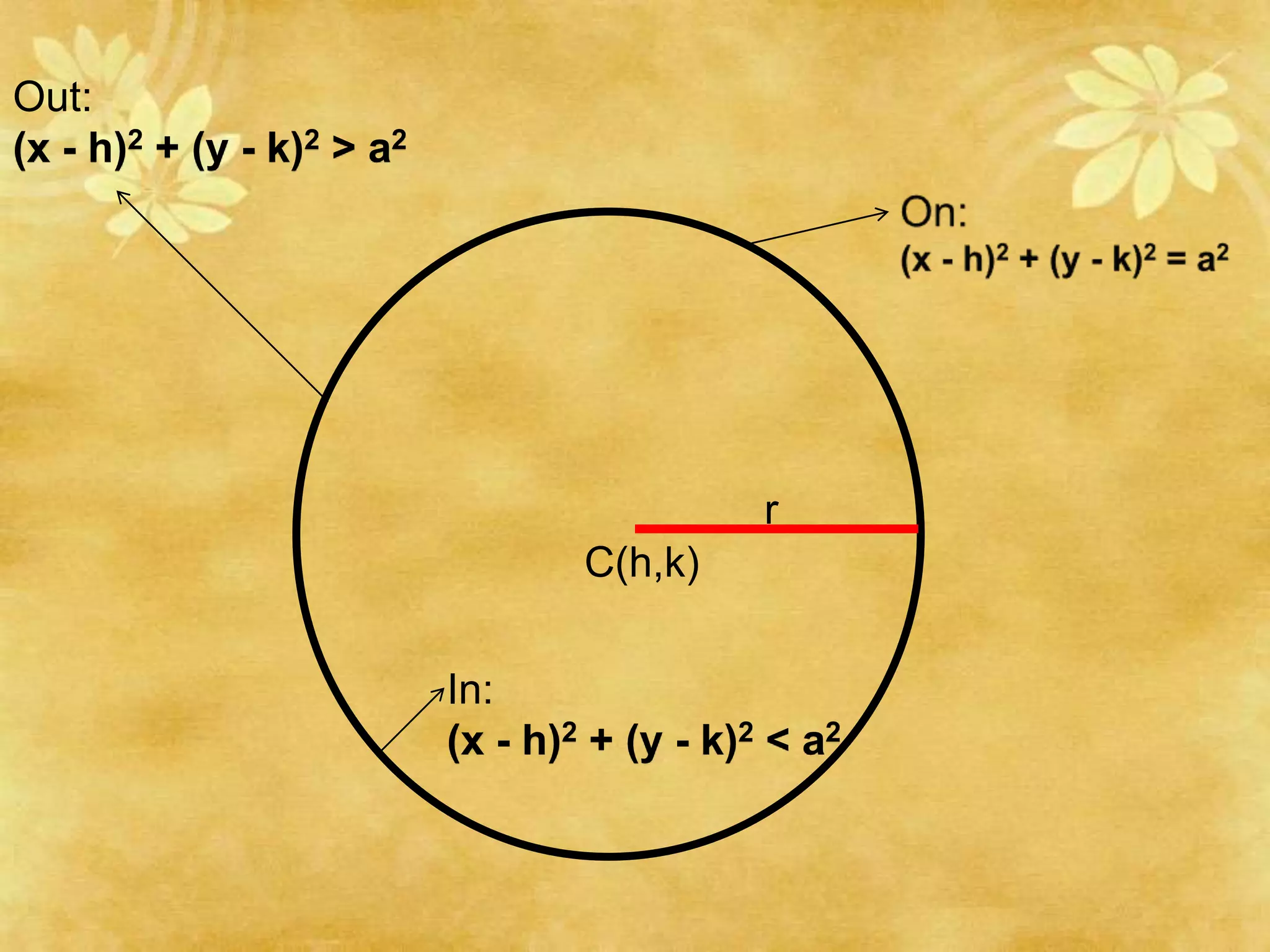
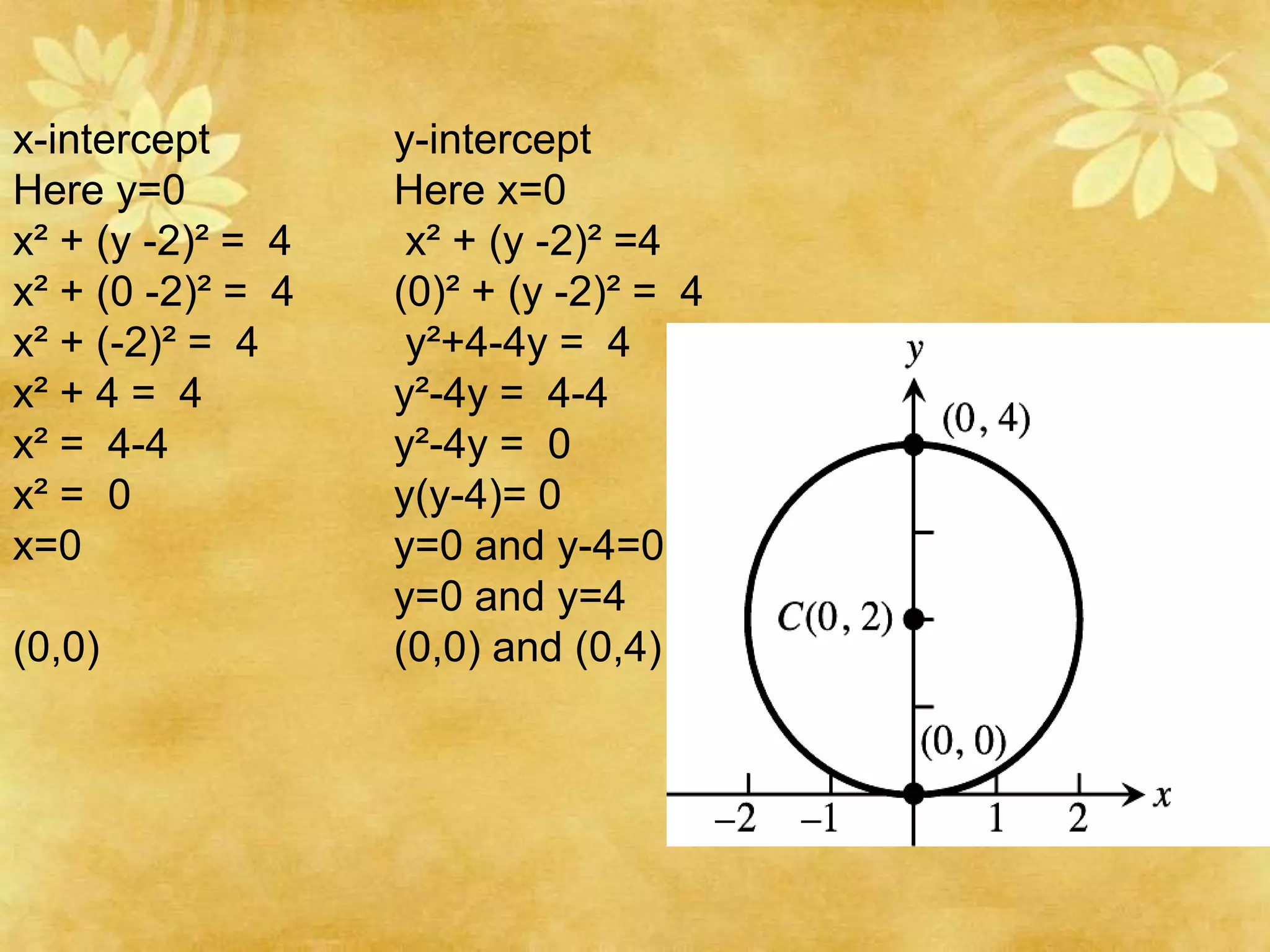
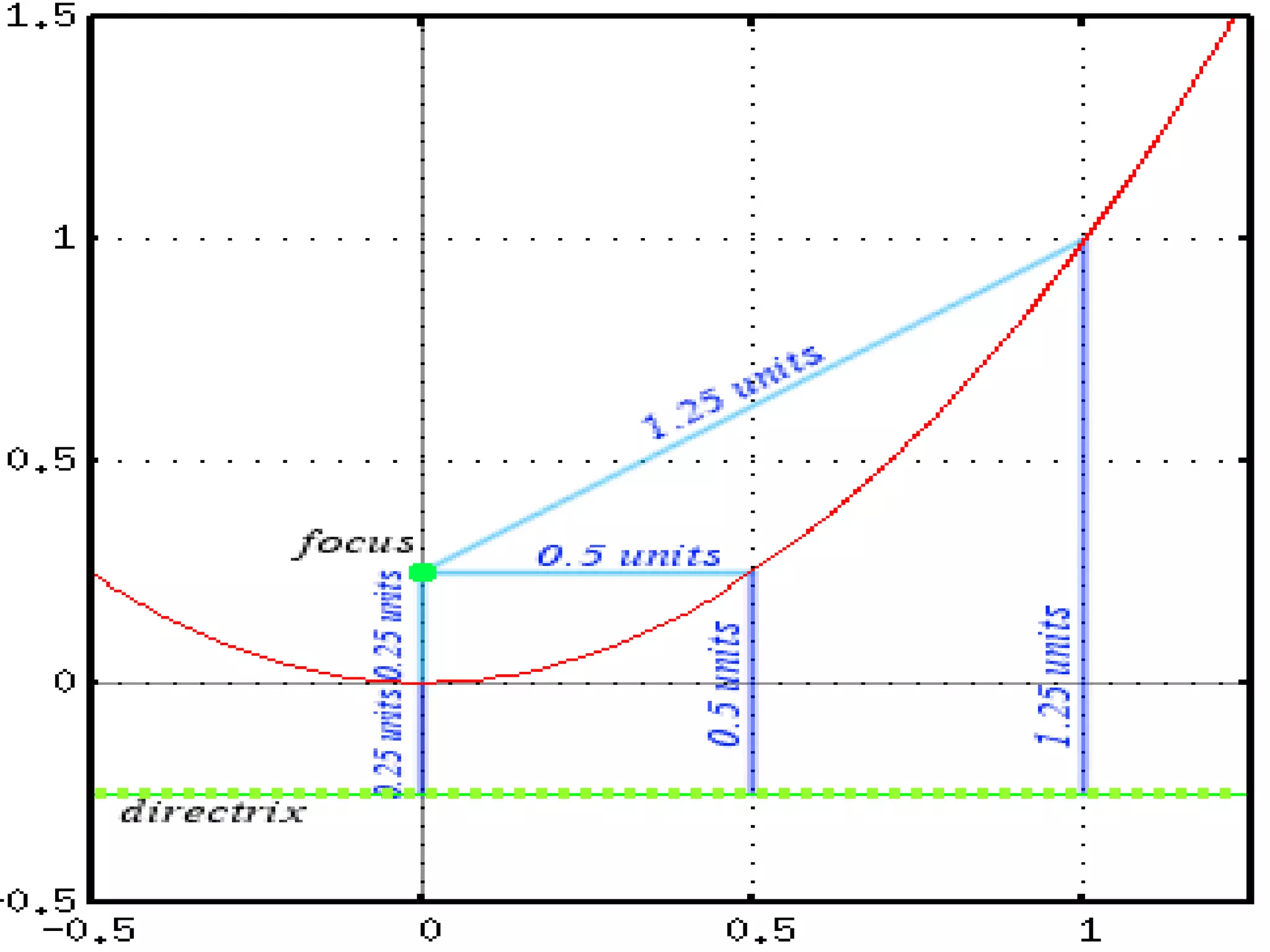
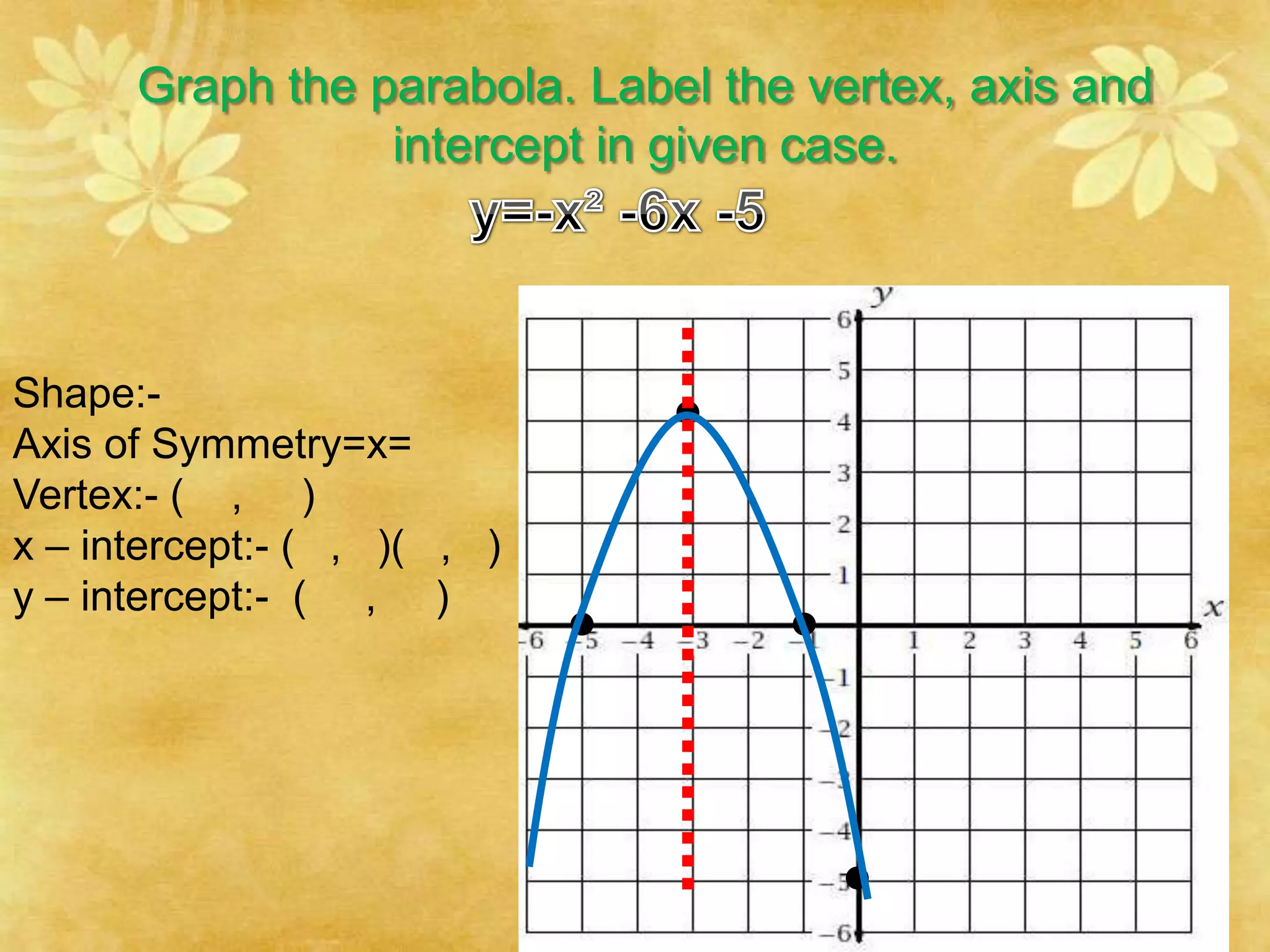
This document provides a summary of topics covered in a pre-calculus final presentation, including quadratic inequalities, circles, and parabolas. It defines quadratic inequalities and how to solve them, provides the standard equation for a circle and how to find the equation of a circle given its center and radius, and defines key properties of parabolas such as their shape, axis of symmetry, vertex, and intercepts. Sample problems are worked through demonstrating how to solve quadratic inequalities, find the equation of a circle, and graph a parabola labeling important features.

2. PRE CALCULUS
FINAL PRESENTATION

3. INTRODUCTION
 GROUP LEADER : MR.M.FAIZAN-UL-HAQ(16076)
 GROUP MEMBER : MR.WARIS SHAH(16052)
MR.ZORAWAR SULTAN (16319)

4. TOPICS
 QUADRATIC INEQUALITIES
 CIRCLE
 PARABOLA

6. QUADRATIC INEQUALITIES
A quadratic inequality is an inequality that
can be written in one of the forms:-
 ax²+bx+c<0
 ax²+bx+c>0
 ax²+bx+c≤0
 ax²+bx+c≥0

7. how do we solve quadratic inequalities
such as
Answer:-
Solution Interval ( , )
Real line
-∞ ∞
0

8. Solve the inequality. Express the solution sets
as intervals or unions of the intervals and show
them on the real line .Use the result √a²=│a│ as
appropriate.
Answer:-
Solution Interval ( , )
Real line
-∞ ∞
0

11. Definition:-
A round plane figure whose boundary
consists of points having equal
distance from the center.

12. The standard equation of a Circle is:-
P(x,y)
a
C(h,k)

13. Out:
(x - h)2 + (y - k)2 > a2
r
C(h,k)
In:
(x - h)2 + (y - k)2 < a2

14. Find an equation for the circle with the given centre
C(h,k) and the radius a.Then sketch the circle in the xy-
plane.Include the circle’s centre in your sketch.Also,
label the circle’s x-and y intercept ,if any,with their
coordinate pairs.
Solution:-
C( 0 , 2), a = 2
C(h , k)
So h=0
k=2
a=2
We know that
(x + h)² + (y - k)² = a²
Putting the values
(x+0)² + (y -2)² = 2²
x² + (y -2)² = 4

15. x-intercept y-intercept
Here y=0 Here x=0
x² + (y -2)² = 4 x² + (y -2)² =4
x² + (0 -2)² = 4 (0)² + (y -2)² = 4
x² + (-2)² = 4 y²+4-4y = 4
x² + 4 = 4 y²-4y = 4-4
x² = 4-4 y²-4y = 0
x² = 0 y(y-4)= 0
x=0 y=0 and y-4=0
y=0 and y=4
(0,0) (0,0) and (0,4)

17. PARABOLA
Any point on a parabola is at an equal
distance from …
 the focus
 the directrix

21.  Equation of Parabola:-
y=ax²+bx+c
 Shape:-
If a is positive then parabola will open
upward.
If a is negative then parabola will open
downward.
 Axis of Symmetry:-
b
x
2a

22.  Vertex (x,y)
here,
x is axis of symmetry
&
y we have to put the values of x in
given equation.
 X and Y intercept:-
x-intercept y-intercept
here y=0 here x=0

23. Graph the parabola. Label the vertex, axis and
intercept in given case.
Shape:-
Axis of Symmetry=x=
Vertex:- ( , )
x – intercept:- ( , )( , )
y – intercept:- ( , )