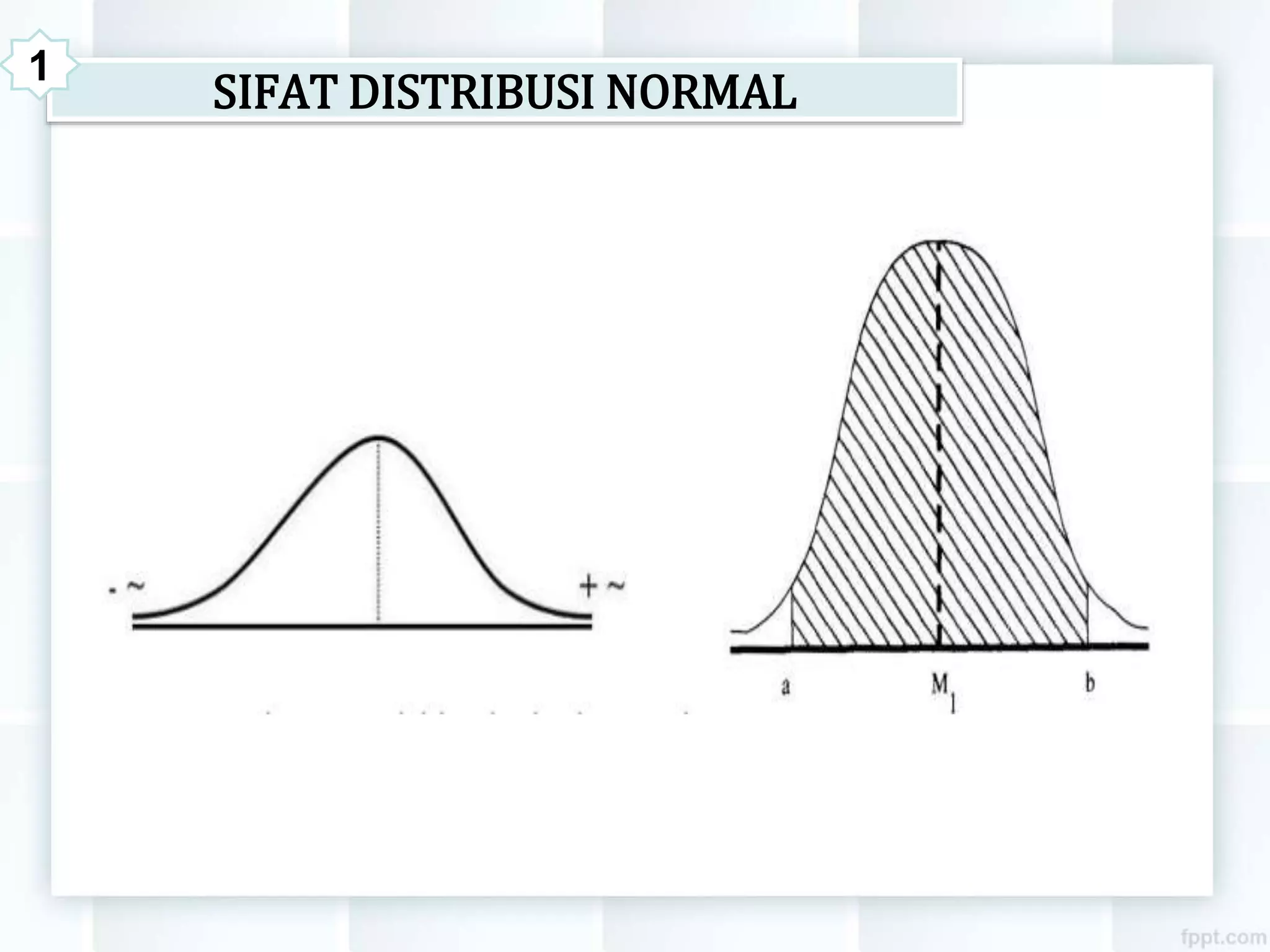
Dokumen ini membahas tiga jenis distribusi probabilitas: binomial, poisson, dan normal. Distribusi binomial melibatkan dua kemungkinan hasil dan sejumlah percobaan tetap, sedangkan distribusi poisson menggambarkan jumlah peristiwa dalam waktu tertentu. Distribusi normal, yang berbentuk distribusi Gaussian, memiliki sifat simetris dan diwakili oleh fungsi kerapatan probabilitas yang khusus.

1. DISTRIBUSI BINOMIAL ,
POISSON DAN NORMAL
Dosen Pembimbing :
Prof.Ratu Ilma Indra Putri
Puji Astuti, M.Sc
Kelompok 10:
Novi Suryani
Shera Annisa
Dhiah Masyitoh

2. DISTRIBUSI BINOMIAL
Definisi :
Distribusi Binomial adalah suatu distribusi
probabilitas yang dapat digunakan
bilamana suatu proses sampling dapat
diasumsikan sesuai dengan proses
Bernoulli.

3. CIRI-CIRI DISTRIBUSI BINOMIAL
Setiap percobaan hanya mempunyai 2
kemungkinan hasil : sukses(hasil yang
dikehendakai, dan gagal (hasil yang tidak
dikehendaki).
Tiap usaha bebas dengan usaha lainnya.
Probabilitas sukses setiap percobaan harus sama,
dinyatakan dengan p. Sedangkan probabilita gagal
dinyatakan dengan q, dan jumlah p dan q harus
sama dengan satu.
Jumlah percobaan, dinyatakan dengan n, harus
tertentu jumlahnya.
1

4. PELUANG DISTRIBUSI BINOMIAL
Peluang distribusi normal dirumuskan sebagai
berikut :
2

5. Untuk mencari
koefisien binomial
dicari dengan rumus :
Dalam distribusi
binomial dikenal
parameter rata-rata
( ) dan simpangan
baku ( ).
PELUANG DISTRIBUSI BINOMIAL
3

6. DISTRIBUSI POISSON
Definisi :
Distribusi Poisson adalah distribusi
probabilitas diskret yang menyatakan
peluang jumlah peristiwa yang terjadi pada
periode waktu tertentu apabila rata-rata
kejadian tersebut diketahui dan dalam
waktu yang saling bebas sejak kejadian
terakhir.

7. CIRI-CIRI DISTRIBUSI POISSON
Percobaan di satu selang tertentu tak bergantung
pada selang lain.
Peluang terjadinya satu percobaan singkat atau
pada daerah yang kecil (jarang terjadi).
Peluang lebih dari satu hasil percobaan akan
terjadi dalam selang waktu singkat tertentu, dapat
diabaikan.
1

8. PROBABILITAS DISTRIBUSI POISSON
Probabilitas dari sebuah distribusi Poisson
dirumuskan sebagai berikut :
2

9. DISTRIBUSI NORMAL
Definisi :
Distribusi normal dikenal juga sebagai
distribusi Gaussian, merupakan salah satu
distribusi peluang kontinu dengan grafik
berbentuk bel/genta.

10. SIFAT DISTRIBUSI NORMAL
Grafiknya selalu ada di atas sumbu datar x
Nilai rata-rata = modus = median
Bentuknya simetrik terhadap sumbu x = μ
Mempunyai satu modus, jadi kurva unimodal,
tercapai pada x = μ sebesar  0,3989
Ujung grafiknya hanya mendekati sumbu x atau
tidak akan bersinggungan maupun berpotongan
dengan sumbu x (berasimtot dengan sumbu x).
Luas daerah grafik selalu sama dengan satu unit
persegi.
1

11. SIFAT DISTRIBUSI NORMAL
1

12. FUNGSI KERAPATAN PROBABILITAS
Fungsi kerapatan probabilitas dari distribusi normal
diberikan dalam rumus berikut:
Keterangan:
f(x)= fungsi densitas peluang normal
π = 3,1416, nilai konstan yang bila ditulis hingga 4 desimal .
e = 2,7183, bilangan konstan, bila ditulis hingga 4 desimal
μ = parameter, rata-rata untuk distribusi.
σ = parameter, simpangan baku untuk distribusi.
Untuk - ∞ < x < ∞, maka dikatakan bahwa variabel acak X berdistribusi
normal.
2