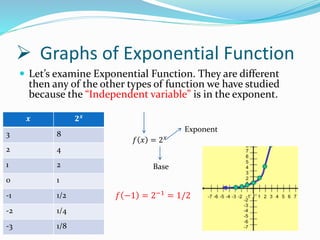
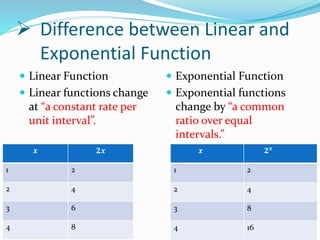
This document discusses linear and exponential functions. It defines a function as relating one variable to another. Linear functions are of the form f(x)=mx+b and form a straight line when graphed. Exponential functions have a constant growth factor, so that a fixed change in x results in multiplication of y by a fixed amount. They take the form of y=abx. The document provides examples and discusses how linear and exponential functions are used in various real-life contexts like saving accounts, loans, and modeling growth.

2. Prepared by Motivational Shining Stars

3.  Function
 A function is a Mathematical process that uniquely
relates the value of “one variable” to the value of “one
(or more) other variables.”
Examples:
𝑠𝑖𝑛(𝑥)
𝑥3 + 𝑥2 + 5𝑥 + 12
𝑒 𝑥
, 2
𝑥 , 𝑥! , cos(𝑥) , tan 𝑥
Function
Y=f(X)
Output variable
“Y”
Input variable
“X”

4.  What Does Linear Mean?
 Linear come from the Latin word LINEARIS which
means “Created by lines”
 If a graph is linear it will form a “Straight”
 A linear function is a function of the
form: f(x)=mx+b
Where, m and b are the real numbers
and m≠0
 Linear expressions consist of only
One variable and no exponents.

5.  Examples:
 y=25x+10
 y=4(3/5)ⁿ
Because of the variable as exponent.
Transform the following into the form y=mx+b
i. x+y=2 ; y=-x+2
ii. -3x+2y=6 ; y=-1.5x+3
 Slope of Linear Function
Slope =
𝑟𝑖𝑠𝑒
𝑟𝑢𝑛
=
𝑦2−𝑦1
𝑥2−𝑥1
Linear function
Non linear function

6.  Expressions of Linear Function
 Standard: Ax+By=C
Point Slope: y-y1=m(x-x1)
Slope intercept: y=mx+b
Slope: y=
𝑦−𝑦1
𝑥−𝑥1

7.  Graphing Linear Functions Using
Points
• Use two points (x,y)
and (x1,y1)
• Find these points on
the graph
• For example,
• Let (x,y)=(1,2)
• and (x1,y1)=(3,4)

8.  Exponential Function
 A function is called an exponential function if it has “a
Constant Growth Factor”
 This means that for a “Fixed” change in (x,y) gets
“Multiplied” by a fixed amount.
 An exponential function is a function of the form
y=𝑎𝑏 𝑥
 Where a≠0, b> 0 and 𝑏 ≠ 1 and the “exponent must
be a variable.”
Remember that
𝑓 𝑥 = 𝑎 𝑥
+ 𝑏

9.  Exponential Function
𝑎 𝑏
= 𝑐
Exponent
Power
Base
𝑎0
= 1, 𝑎 ≠ 0
𝑎1
= 𝑎
𝑎 𝑛
= 𝑎. 𝑎. 𝑎 … . . 𝑎(n times)

10.  Indices Rules:
 𝑎 𝑚
× 𝑎 𝑛
= 𝑎 𝑚+𝑛
 𝑎 𝑚
÷ 𝑎 𝑛
= 𝑎 𝑚−𝑛
 𝑎 𝑛 𝑦 = 𝑎 𝑥𝑦
 𝑎𝑏 𝑛 = 𝑎 𝑛𝑏 𝑛

11.  Examples
 2 𝑥+1=16
 2 𝑥 = 8
 𝑥2 = 25
 𝑥 =9
 3𝑥 −1
 2 𝑥 =
2
2
 22𝑥
− 5𝑥 × 2 𝑥
+ 4 = 0
 16−𝑥
=
1
2
 2 × 35𝑥 =
2
27

12.  Graphs of Exponential Function
 Let’s examine Exponential Function. They are different
then any of the other types of function we have studied
because the “Independent variable” is in the exponent.
𝑓 −1 = 2−1 = 1/2
𝒙 𝟐 𝒙
3 8
2 4
1 2
0 1
-1 1/2
-2 1/4
-3 1/8
𝑓 𝑥 = 2 𝑥
Exponent
Base

13.  Difference between Linear and
Exponential Function
 Linear Function
 Linear functions change
at “a constant rate per
unit interval”.
 Exponential Function
 Exponential functions
change by “a common
ratio over equal
intervals.”
𝒙 𝟐 𝒙
1 2
2 4
3 8
4 16
𝒙 𝟐𝒙
1 2
2 4
3 6
4 8

14.  IS THE EXAMPLE OF LINEAR OR EXPONENTIAL?
• Sebastian deposits $500,000 in a local bank that will pay
out 5% interest every year. Is this example linear or
exponential?
• A certain type of corn grows at the rate of 3 inches per
week. Is this example linear or exponential?
• The Munn Sugar processing plant is able to process 10
tons of sugar per month Assuming that this process stay
steady. Is this example linear or exponential?
• Exercise biologist, Samantha discovered that to reduce
soreness people should start biceps curls at 10 pounds.
Then, progress weekly to 11 pounds, 14 pounds, 20
pounds, 32 pounds, 50 pounds and so on . Is this
example linear or exponential?

15.  Use of Linear and Exponential
Functions in our life
 Use of Linear Function
i. Variable costs
ii. Rates
iii. Budgeting
iv. Making predictions
 Use of Exponential Function
i. Putting money in saving account
ii. Student loans
iii. Radioactive decay

16.  Conclusion
 Linear and exponential functions are the
mathematical process for solving the problems of
algebra .
 These functions plays very important role in Maths
and also our real life.
 By using these functions, we can present our problems
graphically .
 Basically , these are the base of Algebra and
Mathematics.