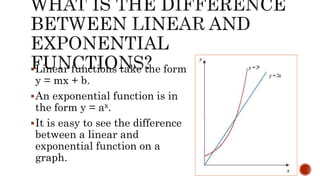
Students will construct, compare, and interpret linear and exponential function models and solve problems involving each model. Key differences are: - Linear functions change at a constant rate per unit interval while exponential functions change by a constant factor over equal intervals. - Linear functions are of the form y=mx+b while exponential functions are of the form y=ax. - Students will determine whether examples describe a linear or exponential pattern of change by analyzing whether the rate of change is constant or changing by a common factor over time.

1. Differentiate between linear and exponential functions.

2. 4 3 2 1 0
In addition to level 3,
students make
connections to other
content areas and/or
contextual situations
outside of math.
Students will construct, compare,
and interpret linear and
exponential function models and
solve problems in context with each
model.
- Compare properties of 2 functions
in different ways (algebraically,
graphically, numerically in tables,
verbal descriptions)
- Describe whether a contextual
situation has a linear pattern of
change or an exponential pattern of
change. Write an equation to model
it.
- Prove that linear functions
change at the same rate over time.
- Prove that exponential functions
change by equal factors over time.
- Describe growth or decay
situations.
- Use properties of exponents to
simplify expressions.
Students will
construct, compare,
and interpret linear
function models and
solve problems in
context with the
model.
- Describe a
situation where one
quantity changes at a
constant rate per unit
interval as compared
to another.
Students will
have partial
success at a 2
or 3, with
help.
Even with help,
the student is not
successful at the
learning goal.
Focus 8 Learning Goal – (HS.N-RN.A.1 & 2, HS.A-SSE.B.3, HS.A-CED.A.2, HS.F-IF.B.4, HS.F-IF.C.8 & 9, and HS.F-LE.A.1) =
Students will construct, compare and interpret linear and exponential function models and
solve problems in context with each model.

3. Linear functions take the form
y = mx + b.
An exponential function is in
the form y = ax.
It is easy to see the difference
between a linear and
exponential function on a
graph.

4. Linear functions
change at a constant
rate per unit
interval.
An exponential
function changes by
a common ratio over
equal intervals.
x 2x
1 2
2 4
3 6
4 8
5 10
6 12
7 14
8 16
9 18
10 20
x 2x
1 2
2 4
3 8
4 16
5 32
6 64
7 128
8 256
9 512
10 1,024

5.  Sebastian deposits $100,000 in a local bank that will pay out 5%
interest every year. Is this example linear or exponential?
 A certain type of corn grows at the rate of 3 inches per week. Is this
example linear or exponential?
 The Munn Sugar Processing Plant is able to process 10 tons of sugar
per month. Assuming that this process stays steady, is this example
linear or exponential?
 Exercise biologist, Samantha, discovered that to reduce soreness,
people should start biceps curls at 10 pounds. Then, progress
weekly to 11 pounds, 14 pounds, 20 pounds, 32 pounds, 56 pounds
and so on. Is this example linear or exponential?