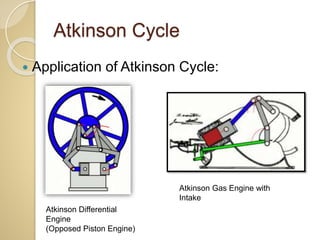
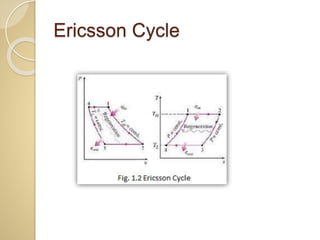
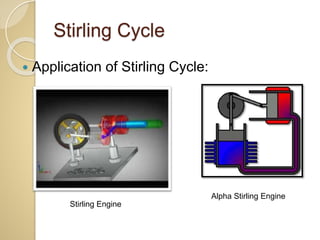
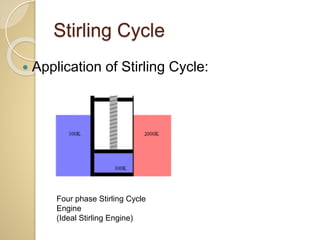
This document discusses three thermodynamic cycles - the Atkinson cycle, Ericsson cycle, and Stirling cycle. The Atkinson cycle consists of two adiabatic and two constant pressure/volume processes. The Ericsson cycle consists of two isothermal and two constant pressure processes. The Stirling cycle consists of two isothermal and two isochoric (constant volume) processes. Applications of each cycle such as engines are also mentioned.

1. Atkinson Cycle, Ericsson Cycle
and Stirling Cycle
-by Group 11
[Dhaval Shukla,
Abhishek Singh R.,
Abhishek Singh
Aman Singh]
-Engineering Thermodynamics
-A.C.E.T.

2. Atkinson Cycle
 The Atkinson cycle was
conceived and developed
by a British engineer, Dr.
James Atkinson.
 This cycle consists of two
adiabatic processes, a
constant volume and a
constant pressure
processes.

3. Atkinson Cycle
 Fig. 1.1, shows the Atkinson cycle plotted
on p-V and T-s diagram.

4. Atkinson Cycle
 The point 1 represents that the cylinder is
full of air with volume V₁, pressure p₁, and
absolute temperature T₁.
a) Process 1-2: This process represents the
isentropic compression of air from state-1
to state-2.
b) Process 2-3: Heat is supplied to the
compressed air at constant volume from
an external source. The pressure rises
and the ratio α=p₃/p₂ is called the
explosion ratio.

5. Atkinson Cycle
c) Process 3-4: The increased high pressure
exerts a greater amount of force on the piston
and pushes it forward. Expansion of working
fluid takes place isentropically up to the
lowest pressure p₁=p₄ of the cycle, and work
is done by the system.
d) Process 4-1: This process represents the
rejection of heat by air at constant pressure.
Hence volume and temperature of air
decreases to initial value. Therefore, a cycle
is completed.

6. Atkinson Cycle
 Calculation of air standard efficiency
Consider ‘m’ kg of air in the cycle.
3 2
4 1
3 2 4 1
Heat supplied at constant volume,
( )
Heat rejected at constant pressure,
( )
Net work done,
Heat supplied - Heat rejected
= ( ) - ( )
S v
R p
net
v p
Q mC T T
Q mC T T
W
mC T T mC T T
 
 

 

7. Atkinson Cycle
 
3 2 4 1
3 2
4 1
3 2
Air standard efficiency,
work done
η=
Heat supplied
( ) ( )
=
( )
γ( )
=1 1
v p
v
mC T T mC T T
mC T T
T T
T T
  


 


8. Atkinson Cycle
γ-1
γ-11
2 1 1
2
γ-13
3 2 2 1
2
From isentropic compression process 1-2,
From constant volume process 2-3,
α=α
From isentropic expansion process 3-4,
V
T T T r
V
p
T T T T r
p
 
  
 
 

9. Atkinson Cycle
 
γ-1 γ-1
3 3 1
4 3 3
4 1 4
γ-1
2 1
3 2 3
1 4
γ-1
3 1
γ-1
4
4
4 1
1
=
=
From constant pressure process 4-1,
V V V
T T T
V V V
V V
T V V
V V
T V
r V
V
T T
V
   
     
   
 
  
 
 
 
 

Q

10. Atkinson Cycle
 
 
 
1
γ
1 1
γ-1 γ-1
1 1
1
γ
γ-1
Substituting the value of temperatures
in equation 1 , we get
1 γ α -
η
α
γ α 1
η 1 2
α -1
T T
T r T r
r
 
   
 

 
 
   
 
 

11. Atkinson Cycle
 Which is the required equation for air
standard efficiency of the cycle.
 The idea of the Atkinson cycle is to get
more work than that given by Otto cycle.
 The area 4 onwards represents this
increased work.
 Further it is to be noted that heat rejection
occurs at lower average temperature (T₅
being higher than T₁).

12. Atkinson Cycle
 This aspects make Atkinson cycle more
efficient than Otto cycle.
 However, it is very difficult to construct
an engine working on Atkinson cycle.

13. Atkinson Cycle
 Application of Atkinson Cycle:
Atkinson Differential
Engine
(Opposed Piston Engine)
Atkinson Gas Engine with
Intake

14. Atkinson Cycle
 Application of Atkinson Cycle:
Rotary Atkinson Cycle
Engine

15. Ericsson Cycle
 The Ericsson cycle is
named after inventor John
Ericsson, who designed and
built many unique heat
engines based on various
thermodynamic cycles.
 He is credited with inventing
two unique heat engine
cycles and developing
practical engines based on

16. Ericsson Cycle
 His first cycle is now known as the closed
Brayton cycle, while his second cycle is
what is now called the Ericsson cycle.
 The Ericsson cycle consists of two
isothermal and two constant pressure
processes.
 The p-V and T-s diagram with the
mainframe structure of Ericsson Cycle is
shown in Fig.1.2:

17. Ericsson Cycle

18. Ericsson Cycle
 The processes taking place in Ericsson
cycle is given below:
a) Process 1-2: At a constant
temperature the pressure of air is
increased, therefore the compression
takes place.
b) Process 2-3: The increased pressure
during this process is maintained and
further heat is added to the cylinder.

19. Ericsson Cycle
c) Process 3-4: Now, the temperature is
again maintained constant and the
volume of air increases. Therefore the
expansion takes place.
d) Process 4-1: Again maintaining the
pressure constant, heat is removed from
the cylinder system. Hence the process
reaches to its initial state, making the
process reversible cyclic process.

20. Ericsson Cycle
 The thermal efficiency of Ericsson Cycle is
given below:
thη
1
,
H L
H
L
H
H
L
T T
T
T
T
where T Higher Temperature
and T Lower Temperature


 



21. Ericsson Cycle
 Application of Ericsson Cycle:
Ericsson Engine
Ericsson Cycle
Engine

22. Stirling Cycle
 The Stirling cycle was
introduced by Dr. Robert
Stirling over the
improvement of ideal
Otto and Diesel cycles.
 The Stirling cycle is
a thermodynamic
cycle that describes the
general class of Stirling
devices.

23. Stirling Cycle
 The Stirling cycle consists of two
isothermal and two isochoric processes.
 The p-V and T-s diagrams of Stirling cycle
has been given below:

24. Stirling Cycle
 The processes occurring in a Stirling
Cycle is given below:
a) Process 1-2: The volume of gas
increases at a constant temperature.
Therefore, the process is called
isothermal expansion process.
b) Process 2-3: The increased volume now
is maintained constant and heat removal
is offered. Therefore, the process is
called Isochoric heat-removal process.

25. Stirling Cycle
c) Process 3-4: In this process again
temperature is maintained constant and
pressure increases. Therefore,
isothermal compression takes place.
d) Process 4-1: Now, the heat is added at
a constant volume. Therefore, the
process is called isochoric heat addition
process. Hence, the process reaches to
its initial state. Therefore, cycle is
completed.

26. Stirling Cycle
 The thermal efficiency of Stirling Cycle is
given below:
thη
1
,
H L
H
L
H
H
L
T T
T
T
T
where T Higher Temperature
and T Lower Temperature


 



27. Stirling Cycle
 Application of Stirling Cycle:
Stirling Engine
Alpha Stirling Engine

28. Stirling Cycle
 Application of Stirling Cycle:
Four phase Stirling Cycle
Engine
(Ideal Stirling Engine)

29. Thank you!