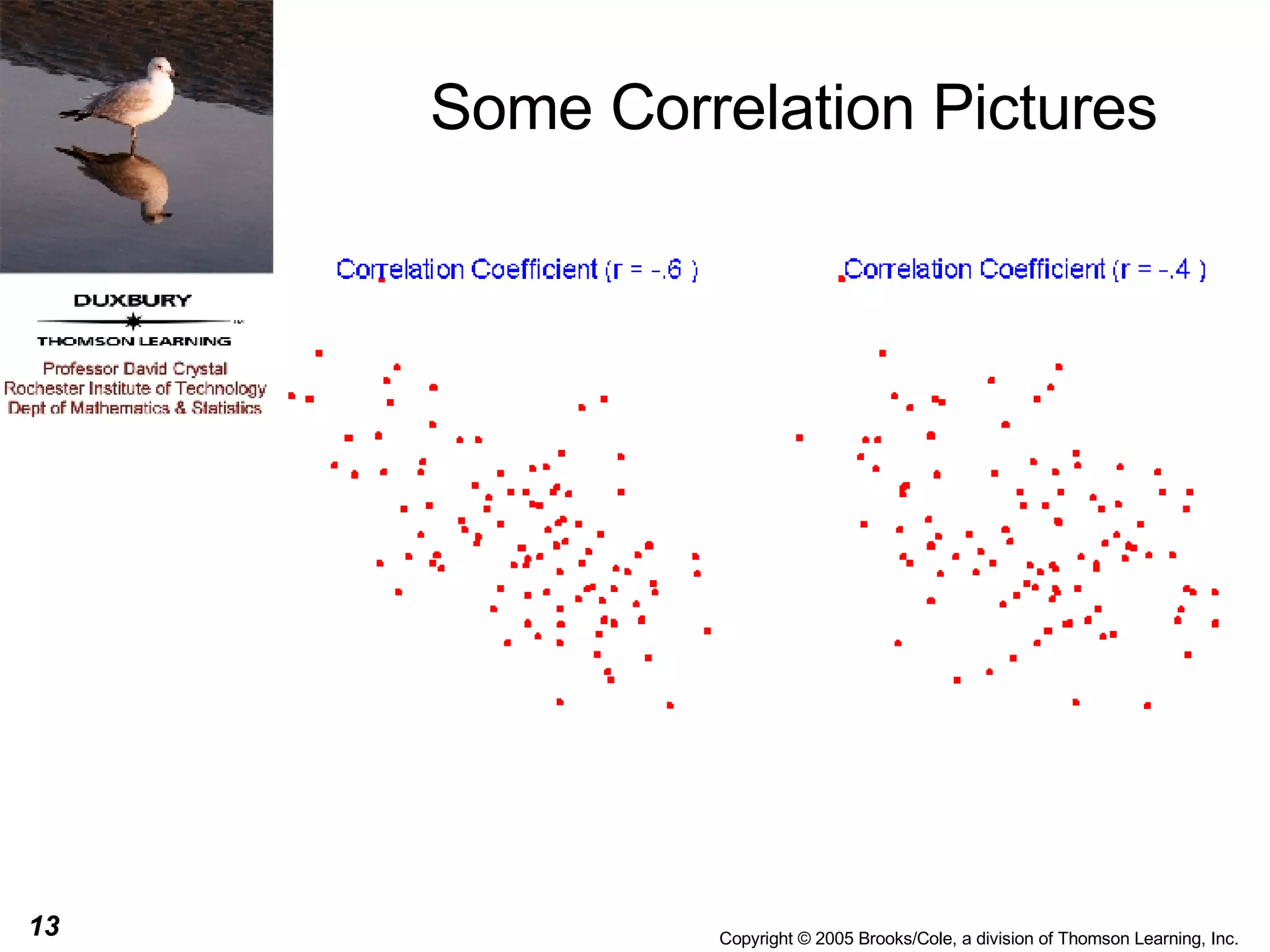
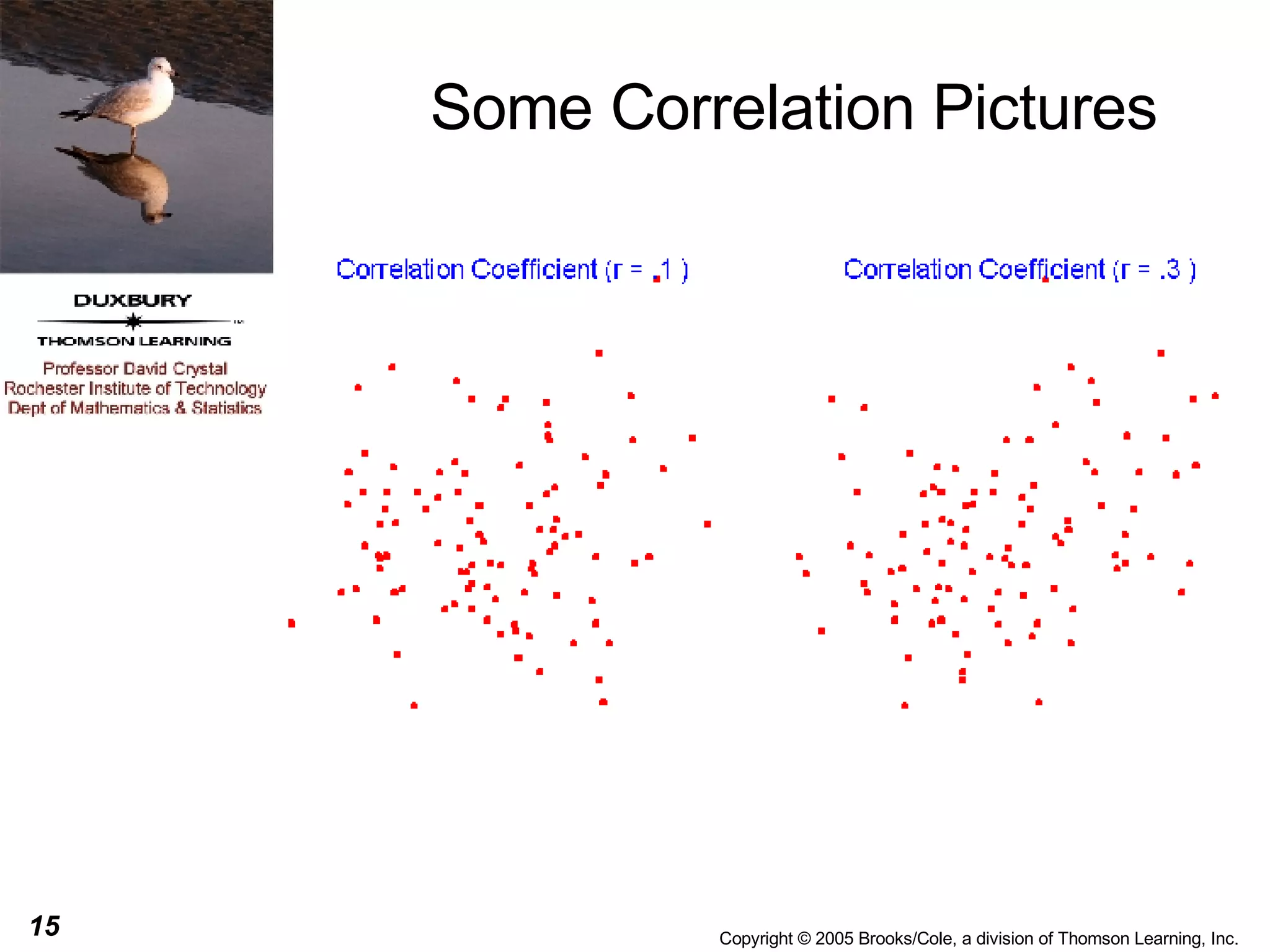
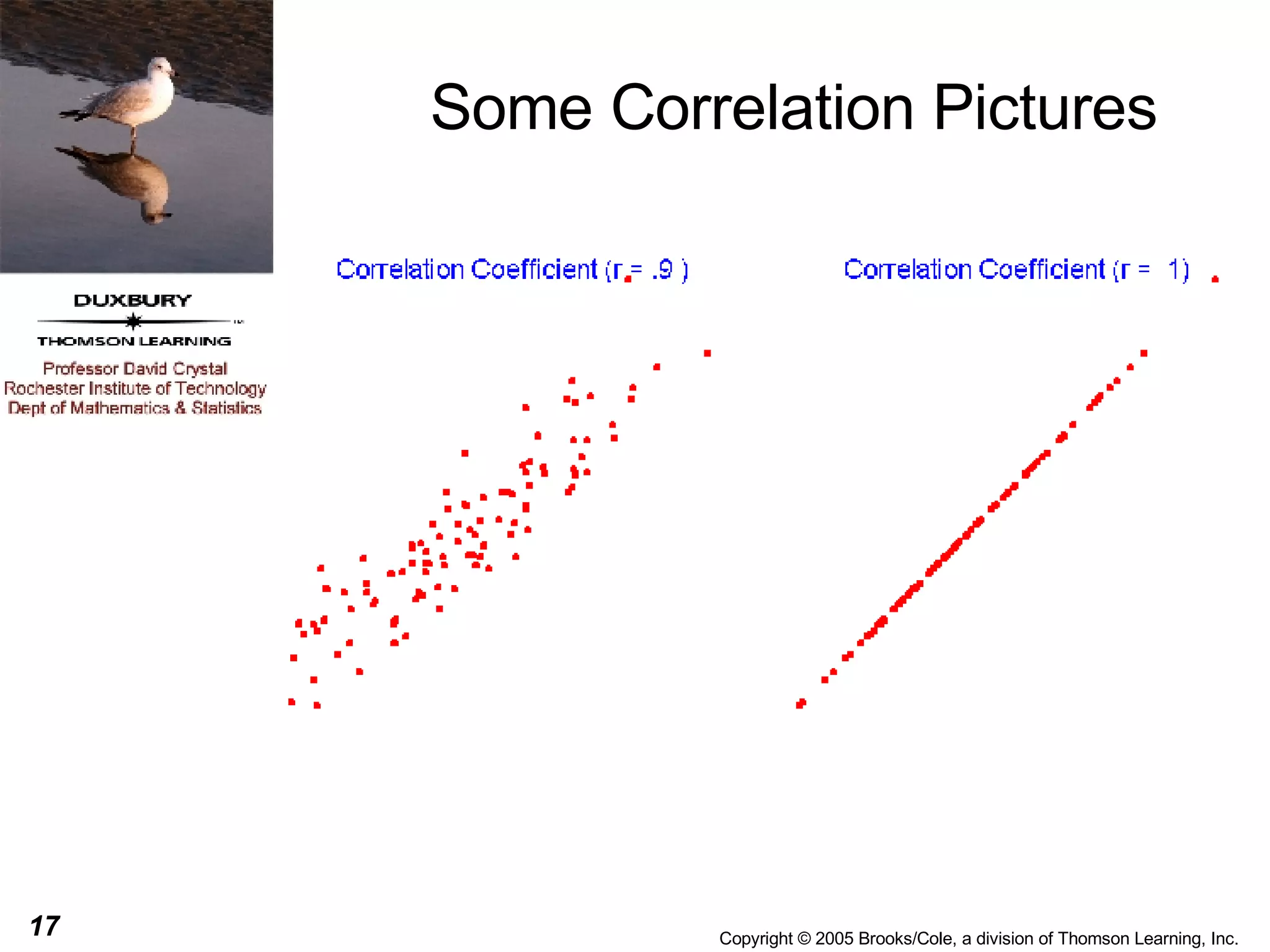
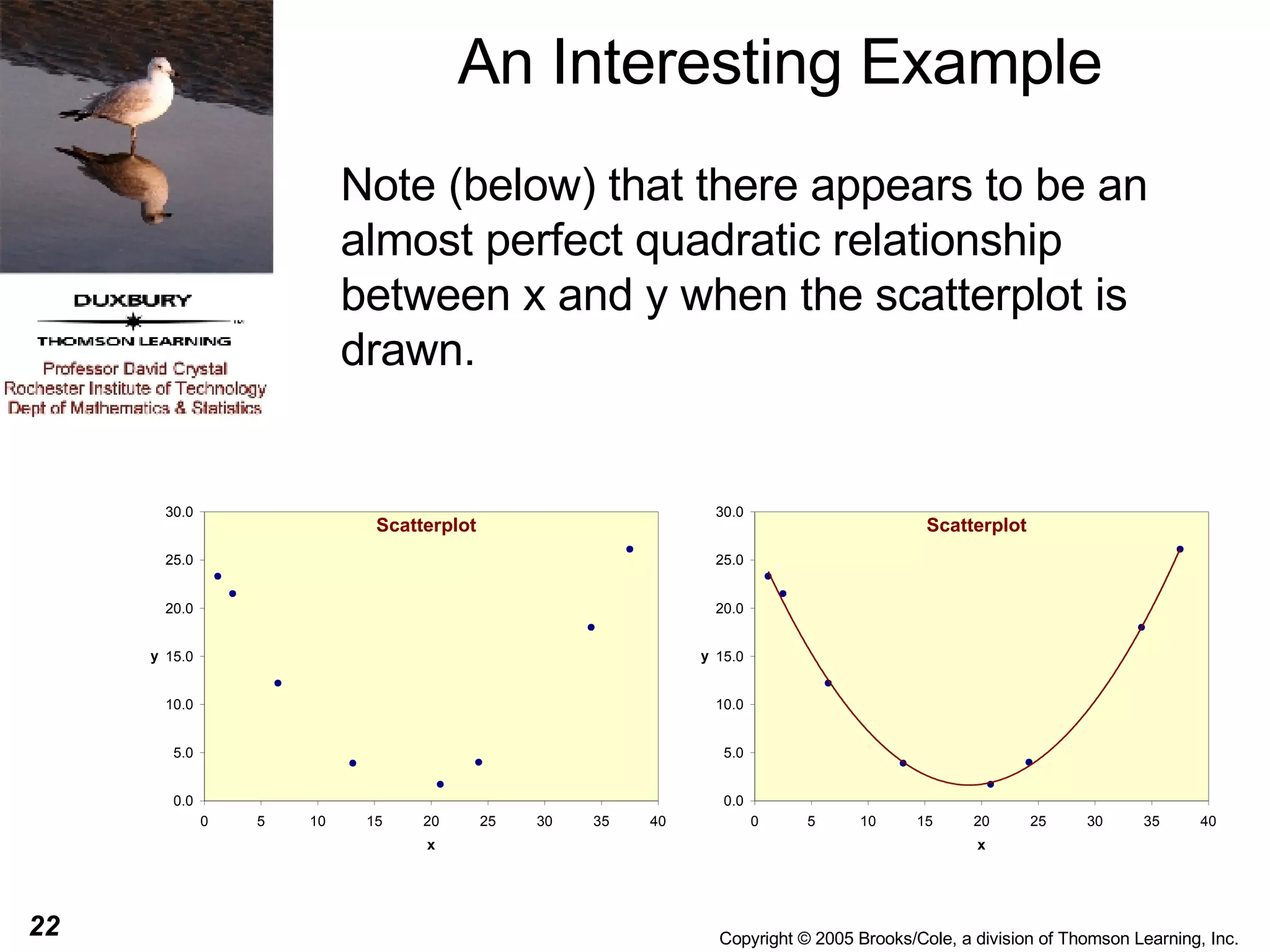
This document discusses summarizing bivariate data using scatterplots and correlation. It provides an example of fare data from a bus company that is modeled using linear and nonlinear regression. Linear regression finds a strong positive correlation between distance and fare, but the relationship is better modeled nonlinearly using the logarithm of distance. The nonlinear model accounts for 96.9% of variation in fares compared to 84.9% for the linear model.





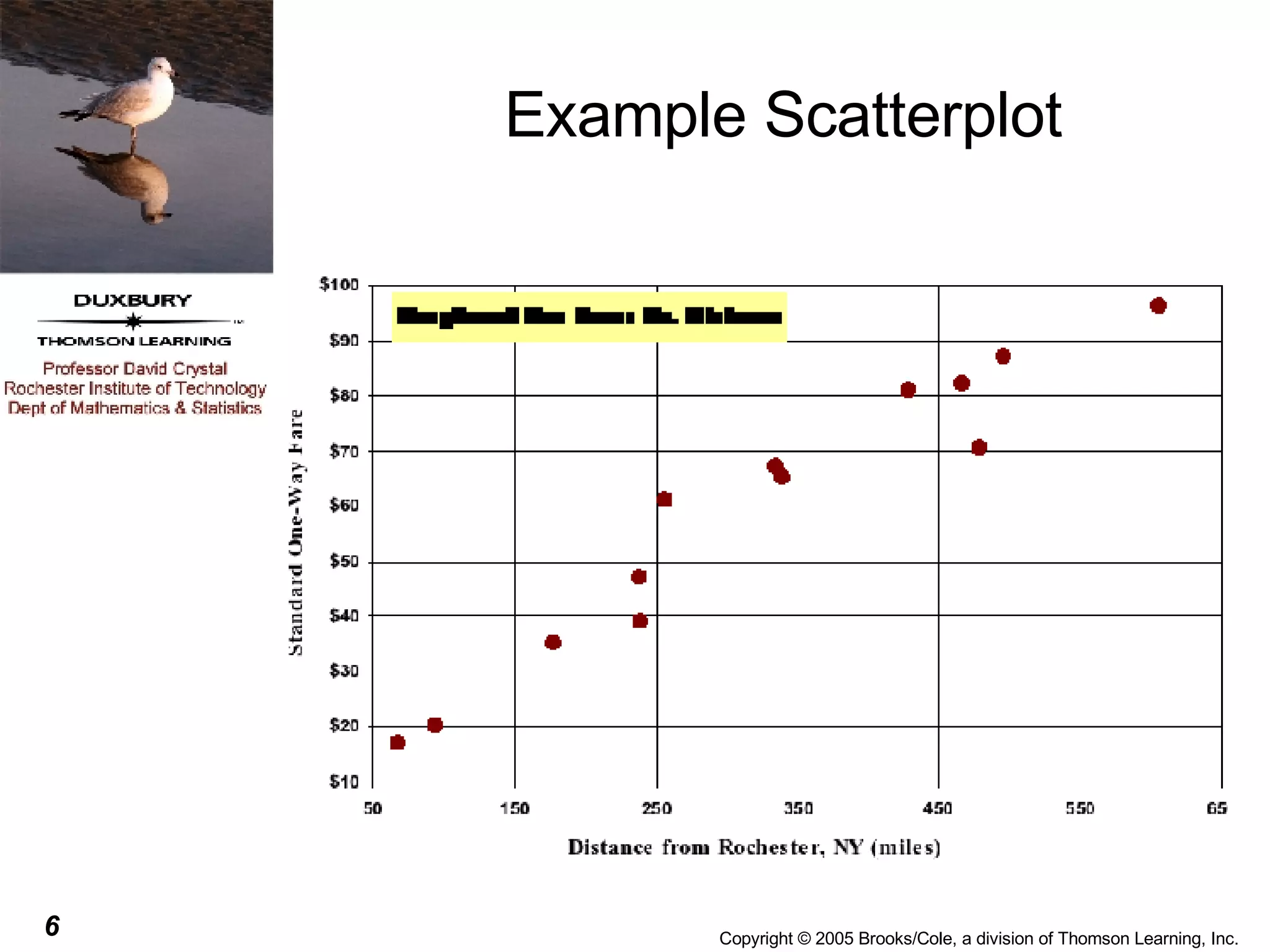






































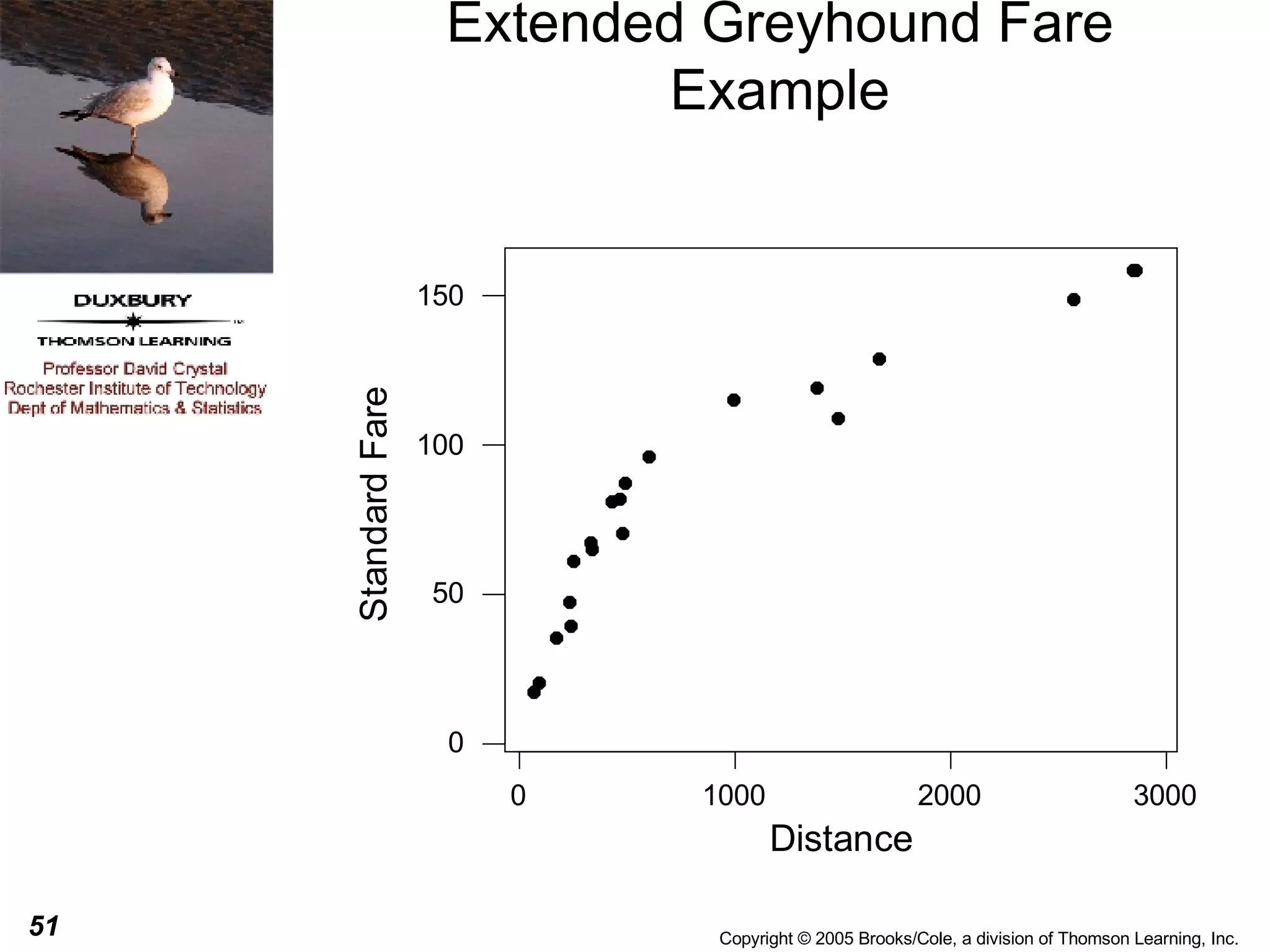

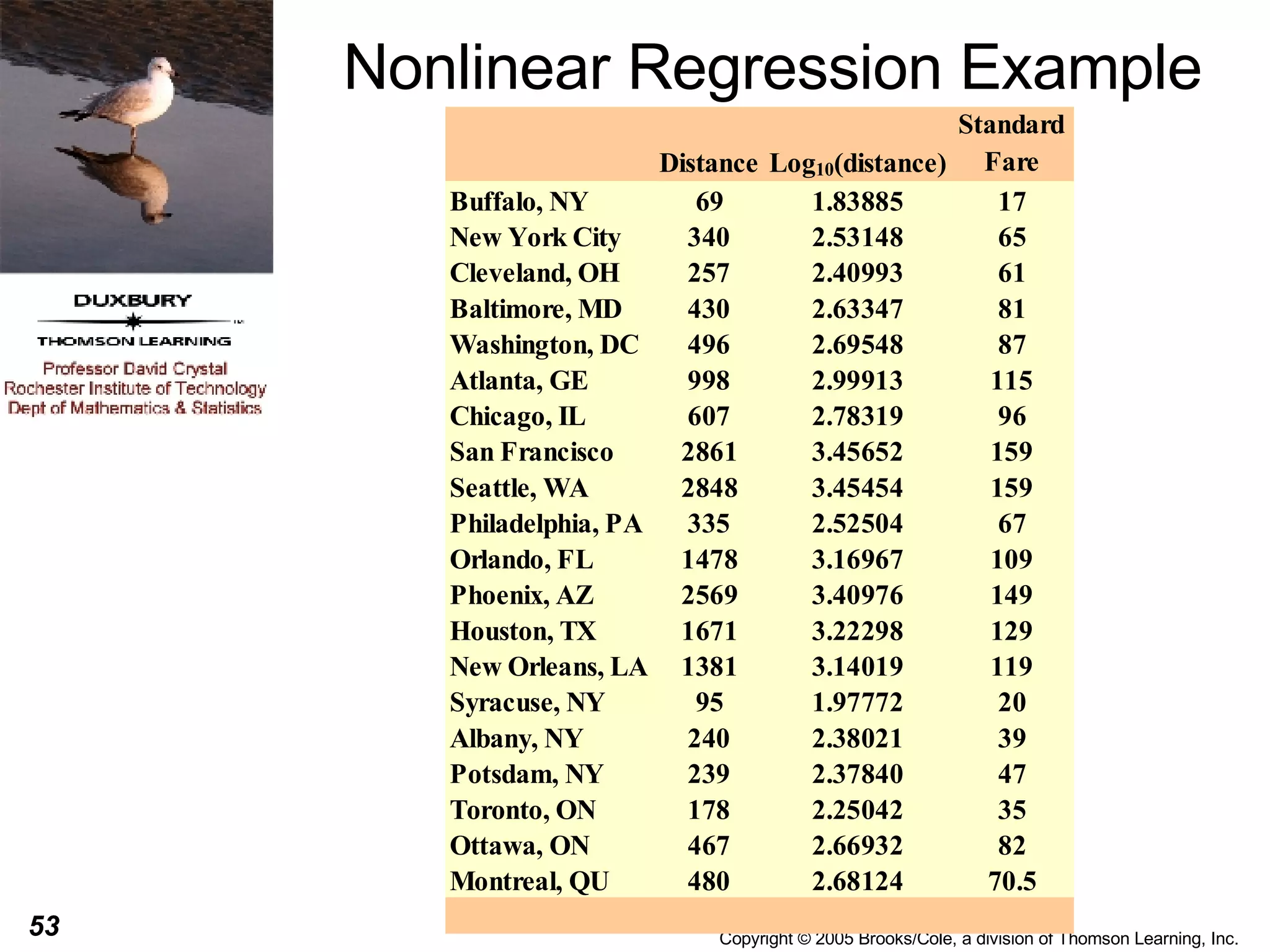
![Nonlinear Regression Example From the previous slide we can see that the plot does not look linear, it appears to have a curved shape. We sometimes replace the one of both of the variables with a transformation of that variable and then perform a linear regression on the transformed variables. This can sometimes lead to developing a useful prediction equation. For this particular data, the shape of the curve is almost logarithmic so we might try to replace the distance with log 10 (distance) [the logarithm to the base 10) of the distance].](https://image.slidesharecdn.com/chapter051761/75/Chapter05-54-2048.jpg)




