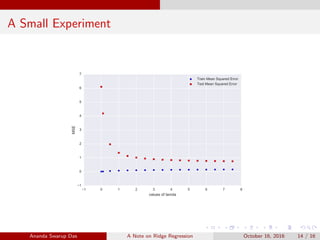
Ridge regression is a technique used for linear regression when the number of predictor variables is greater than the number of observations. It addresses the problem of overfitting by adding a regularization term to the loss function that shrinks large coefficients. This regularization term penalizes coefficients with large magnitudes, improving the model's generalization. Ridge regression finds a balance between minimizing training error and minimizing the size of coefficients by introducing a tuning parameter lambda. The document includes an experiment demonstrating how different lambda values affect the variance and mean squared error of the ridge regression model.

1. A Note on Ridge Regression
Ananda Swarup Das
October 16, 2016
Ananda Swarup Das A Note on Ridge Regression October 16, 2016 1 / 16

2. Linear Regression
1 Linear Regression is a simple approach for Supervised Learning and is
used for quantitative predictions.
2 Assuming X to be a quantitative predictor and y to be a quantitative
response and the relationship between the predictor and the response
to be linear, the linear relationship can be written as
y ≈ β0 + β1X (1)
3 The relationship is represented as an approximate one as it is assumed
that y = β0 + β1X + where is an irreducible error that might have
crept in while recording the data.
Ananda Swarup Das A Note on Ridge Regression October 16, 2016 2 / 16

3. Linear Regression Continued
1 In Equation 1, β0, β1 are two unknown constants, also known as
parameters.
2 Our objective is to use training data and estimate the values of ˆβ0, ˆβ1
3 So far we have discussed the case of simple linear regression. In case
of multiple linear regression, our linear regression model takes the
form
y = β0 + β1x1 + β2x2 + . . . + βpxp + (2)
4 A commonly used technique to find the estimates of the
co-efficients(parameters) is least square method [1].
Ananda Swarup Das A Note on Ridge Regression October 16, 2016 3 / 16

4. How good is our Estimation of the parameters
1 In the regression setting, a technique to measure the fit is
mean-squared error which is given as
MSE =
1
n
n
i=1
(yi − ˆf (xi ))2
(3)
Here, n is the number of observations, yi is the true response and
ˆf (xi ) is the response predicted by our model defined by the
co-efficients estimated by the training data.
Ananda Swarup Das A Note on Ridge Regression October 16, 2016 4 / 16

5. The Bias-Variance Trade Off
As stated in [1], the expected value of the residual error (yi − ˆf (xi )) is
given by
E(yi − ˆf (xi ))2
= Var(ˆf (xi )) + [Bias(ˆf (xi ))]2
+ Var( ) (4)
1 In the above equation, the first term on the right hand side denotes
the variance of the model that is the amount by which ˆf would
change if the parameters β1, . . . , βp are estimated using different
training data.
2 The second term denotes the error introduced by approximating a
may-be complicated real-life model with a simpler model.
Ananda Swarup Das A Note on Ridge Regression October 16, 2016 5 / 16

6. The Bias-Variance Trade Off Continued
Also shown in [1], the expected value of residual error (yi − ˆf (xi )) can also
be expressed as
E(yi − ˆf (xi ))2
= E(f (xi ) + − ˆf (xi ))2
= [f (xi ) − ˆf (xi )]2
+ Var( ) (5)
Notice that we have replace yi = f (xi ) + . The first part [f (xi ) − ˆf (xi )]2
is reducible and we want our estimation of parameters be such that ˆf (xi )
is as close as possible to f (xi ). However, the Var( ) is irreducible.
Ananda Swarup Das A Note on Ridge Regression October 16, 2016 6 / 16

7. What do we reduce
1 Reconsider the Equation 4,
E(yi − ˆf (xi ))2 = Var(ˆf (xi )) + [Bias(ˆf (xi ))]2 + Var( ), the expected
value of MSE cannot be less than Var( ).
2 Thus, we have to try to reduce the variance and the bias for the
model ˆf .
Ananda Swarup Das A Note on Ridge Regression October 16, 2016 7 / 16

8. Certain Situations
Provided the true relationship between the predictor and the response is
linear, the least square method will have less bias.
1 If the size of the training data, n is very very large compared to the
number of predictors that is n >> p, the least square estimates tend
to have less variance.
2 If the size of the training data, n is slightly larger than p, then the
least square estimates may have high variance.
3 If n < p, least square method should not be applied without using
dimension reducing techniques.
Ananda Swarup Das A Note on Ridge Regression October 16, 2016 8 / 16

9. Ridge Regression
1 In this presentation, we will deal with the second situation where n is
slightly greater than p using Ridge Regression which has been found
to be significantly helpful in dealing with variance.
2 In the least square method, coefficients β1 . . . βp are estimated by
minimizing Residual Sum of Squares(RSS)
RSS = n
i=1(yi − β0 − p
j=1 βj xi,j )2. Notice that β0 = y , the mean
of all the responses.
3 In case of Ridge Regression, the minimization function changes to
n
i=1(yi − β0 − p
j=1 βj xi,j )2 + λ p
j=1 β2
j . The λ is a tuning
parameter which constraints the choices of the coefficients, but
decreases the variance. To minimize the objective function, both the
additive terms are to be minimized.
Ananda Swarup Das A Note on Ridge Regression October 16, 2016 9 / 16

10. The Significance of the choice of λ
1 Stated in [1], for every value of λ there exists a constant s such that
the problem of ridge regression coefficient estimation boils down to
minimize
n
i=1
(yi − β0 −
p
j=1
βj xi,j )2
(6)
s.t p
j=1 β2
j ≤ s
2 Notice that if p = 2, under the constaint p
j=1 β2
j ≤ s, ridge
regression coefficient estimation is equivalent to finding the
coefficients lying within a circle (in general a sphere) centered at the
origin and is of radius
√
s, such that the Equation 6 is minimized.
Ananda Swarup Das A Note on Ridge Regression October 16, 2016 10 / 16

11. Ridge Regression Coefficient Estimation
B1
B2
Figure: The Residual Square of Sum(RSS)
n
i=1(yi − β0 −
p
j=1 βj xi,j )2
is a
convex function and when p = 2, the contours look like a set of concentric
ellipses. The least square solution is denoted by the innermost marron dot. The
ellipses centered at that dot have constant RSS thats is all points on a given
ellipses share the common value of RSS which is equal to the Var( ). As the
ellipses expand away from the least square estimate, the RSS increases.
Ananda Swarup Das A Note on Ridge Regression October 16, 2016 11 / 16

12. Ridge Regression Coefficient Estimation
B1
B2
Figure: In general, the ridge regression coefficient estimates are given by the first
point at which the ellipse contacts the constraint circle,the green point in the
above Figure.
Ananda Swarup Das A Note on Ridge Regression October 16, 2016 12 / 16

13. A Small Experiment
1 I am using Python scikit-learn for the purpose of the experiment and
in this context, it must be mentioned that the book by Sebastian
Raschka, Python Machine Learning, PACKT Publishing is a good
book to understand how to use scikit-learn effectively.
2 The data set that is used for the experiment can be found from
https://archive.ics.uci.edu/ml/datasets/Housing.
3 The data set comprises of 506 samples and 14 attributes. I have used
11 attributes as predictors (column number: 1,2,3,5,6,8,9,10,11,12,13
). I have used column number 14 as the responses.
4 Since 506 >> 11, and we are trying Ridge regression for the setting
where n is slightly larger than p, I have randomly selected 20
observations from the data set of which 14 has been used for training
and 6 has been used for testing.
Ananda Swarup Das A Note on Ridge Regression October 16, 2016 13 / 16

14. A Small Experiment
1 0 1 2 3 4 5 6 7 8
values of lamda
1
0
1
2
3
4
5
6
7MSE
Train Mean Squared Error
Test Mean Squared Error
Ananda Swarup Das A Note on Ridge Regression October 16, 2016 14 / 16

15. A Small Experiment
1 Notice that when λ = 0, the minimization function which is
minimize( n
i=1(yi − β0 − p
j=1 βj xi,j )2 + λ p
j=1 β2
j ) is equal to
minimize( n
i=1(yi − β0 − p
j=1 βj xi,j )2), the case of least square
estimation. Notice the differences between the MSEs of test data vs
training data. A sharp/large difference denote significance variance of
our model. Notice the difference between the MSE of the test and
the train data at λ = 0. As the value of λ increase, the variance
decreases up-to λ = 4.
2 In general, the choice of λ can be done through grid search using the
inbuilt module linear−model.RidgeCV from scikit-learn.
Ananda Swarup Das A Note on Ridge Regression October 16, 2016 15 / 16

16. Citations
G. James, D. Witten, T. Hastie, and R. Tibshirani.
An Introduction to Statistical Learning: with Applications in R.
Springer Texts in Statistics. Springer New York, 2014.
Ananda Swarup Das A Note on Ridge Regression October 16, 2016 16 / 16