Embed presentation
Downloaded 14 times












e is a special mathematical constant approximately equal to 2.71828, discovered by Euler. It is the base of the natural logarithm and is used in exponential functions of the form f(x) = aerx to model growth and decay. The value of e can be evaluated using calculators and exponential functions involving e can be graphed by plotting points and shifting the parent graph as needed.













Explains the mathematical constant e (approx. 2.718) discovered by Leonhard Euler, and its classification as a natural base.
Discussion on the approximation of e and its irrational nature, as n approaches infinity.
Teaches how to simplify expressions with the natural base e using exponent rules.
Interactive slide encouraging students to simplify expressions involving the natural base e.
Instructions on using a calculator to evaluate expressions involving e, providing specific examples.
Introduces the form f(x) = ae^rx, differentiating between exponential growth and decay based on r.
Guidance on plotting natural base functions, focusing on selecting points and shifting the graph.
Shows examples of graphing with a focus on identifying the domain and range of natural base functions.
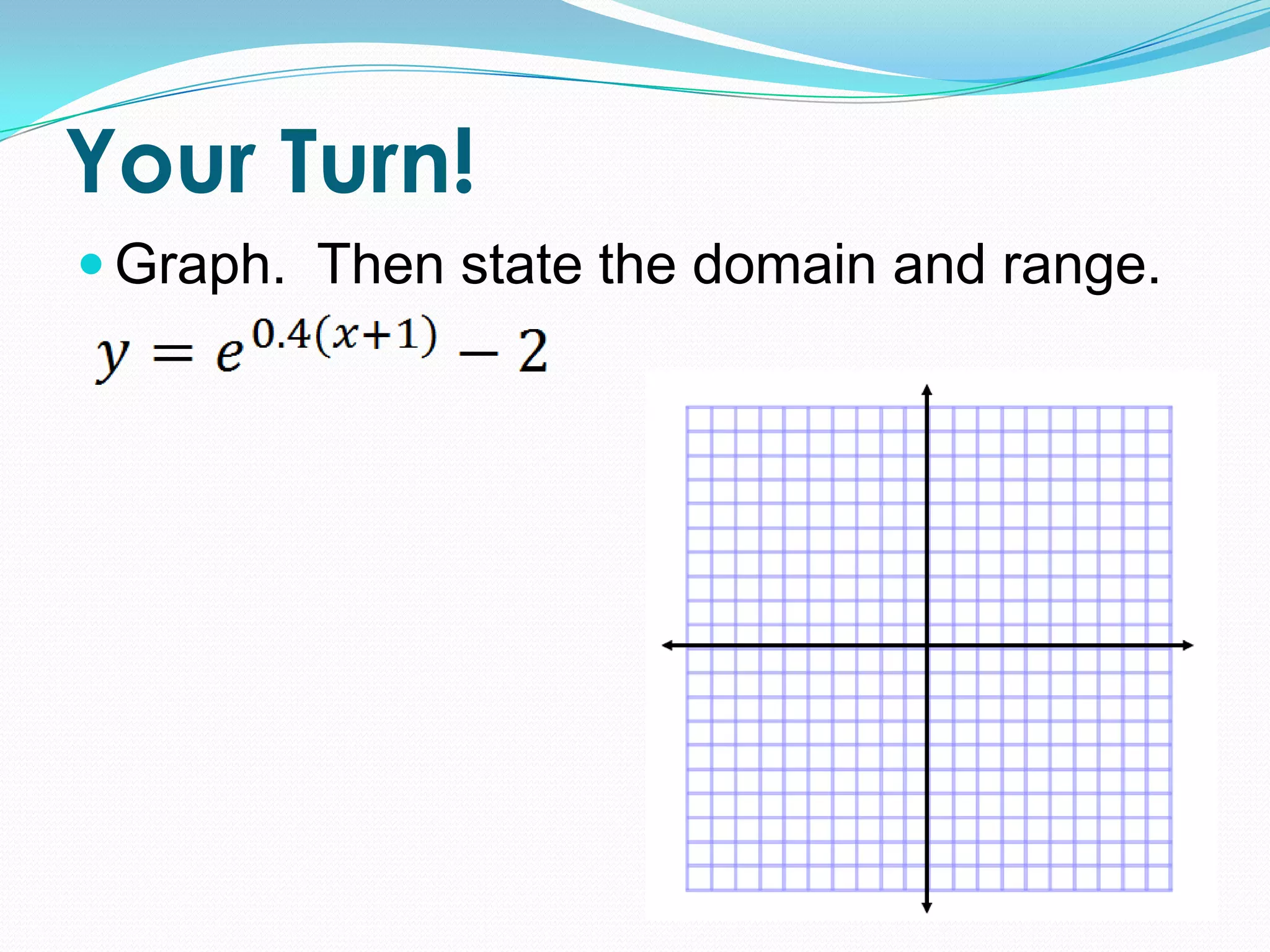
Engagement slide where students graph functions and determine the domain and range.
Discusses continuous compounding as n approaches infinity, explaining the mathematical foundation.
Calculates the balance after 1 year for a $1000 deposit at 8% interest compounded continuously.
Encourages students to calculate the balance for a $1500 deposit at 7.5% interest compounded continuously.