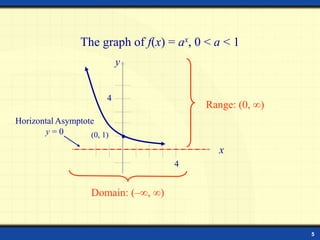
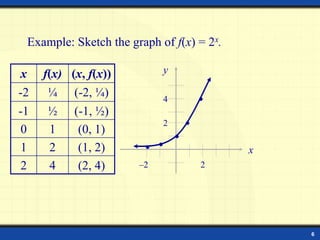
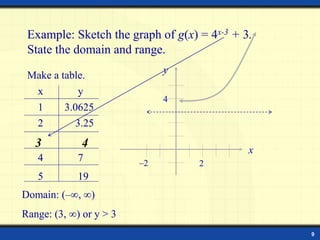
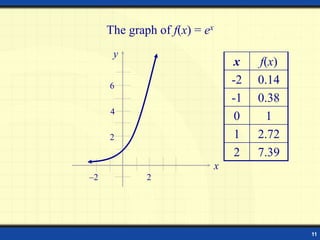
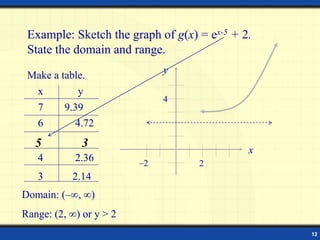
This document discusses exponential functions and their graphs. It defines the exponential function f(x) = ax and gives examples. It shows how to evaluate exponential functions at different values of x. It explains the graphs of exponential functions with bases greater than and less than 1, and how they have horizontal asymptotes at y = 0. It provides examples of sketching graphs of exponential functions and stating their domains and ranges. It introduces the irrational number e and the natural exponential function f(x) = ex. It concludes with formulas for compound interest and an example problem.

1. Exponential Functions and
Their Graphs
Digital Lesson

2. 2
The exponential function f with base a is
defined by
f(x) = ax
where a > 0, a  1, and x is any real number.
For instance,
f(x) = 3x and g(x) = 0.5x
are exponential functions.

3. 3
The value of f(x) = 3x when x = 2 is
f(2) = 32 =
The value of g(x) = 0.5x when x = 4 is
g(4) = 0.54 =
The value of f(x) = 3x when x = –2 is
9
1
9
f(–2) = 3–2 =
0.0625

4. 4
The graph of f(x) = ax, a > 1
y
x
(0, 1)
Domain: (–, )
Range: (0, )
Horizontal Asymptote
y = 0
4
4

5. 5
The graph of f(x) = ax, 0 < a < 1
y
x
(0, 1)
Domain: (–, )
Range: (0, )
Horizontal Asymptote
y = 0
4
4

6. 6
Example: Sketch the graph of f(x) = 2x.
x
x f(x) (x, f(x))
-2 ¼ (-2, ¼)
-1 ½ (-1, ½)
0 1 (0, 1)
1 2 (1, 2)
2 4 (2, 4)
y
2
–2
2
4

7. 7
Example: Sketch the graph of g(x) = 2x – 1. State the
domain and range.
x
y
The graph of this
function is a vertical
translation of the
graph of f(x) = 2x
down one unit .
f(x) = 2x
y = –1
Domain: (–, )
Range: (–1, )
2
4

8. 8
Example: Sketch the graph of g(x) = 2-x. State the
domain and range.
x
y
The graph of this
function is a
reflection the graph
of f(x) = 2x in the y-
axis.
f(x) = 2x
Domain: (–, )
Range: (0, ) 2
–2
4

9. 9
Example: Sketch the graph of g(x) = 4x-3 + 3.
State the domain and range.
x
y
Make a table.
Domain: (–, )
Range: (3, ) or y > 3
2
–2
4
x y
3 4
2 3.25
1 3.0625
4 7
5 19

10. 10
The irrational number e, where
e  2.718281828…
is used in applications involving growth and
decay.
Using techniques of calculus, it can be shown
that









 n
e
n
n
as
1
1
The Natural Base e

11. 11
The graph of f(x) = ex
y
x
2
–2
2
4
6
x f(x)
-2 0.14
-1 0.38
0 1
1 2.72
2 7.39

12. 12
Example: Sketch the graph of g(x) = ex-5 + 2.
State the domain and range.
x
y
Make a table.
Domain: (–, )
Range: (2, ) or y > 2
2
–2
4
x y
5 3
6 4.72
7 9.39
4 2.36
3 2.14

13. 13
Formulas for Compound Interest—
1.) compound per year -- A = P 1 + r nt
n
Interest Applications
Balance in account Principal ($ you invest)
r is the rate
n is the number times you
compound your money per
year
t is time.
2. Compounded continuously– A = Pert

14. 14
A total of $12000 is invested at an annual
interest rate of 9%. Find the balance after
5 years if it is compounded
a. quarterly
b. monthly
c. continuously