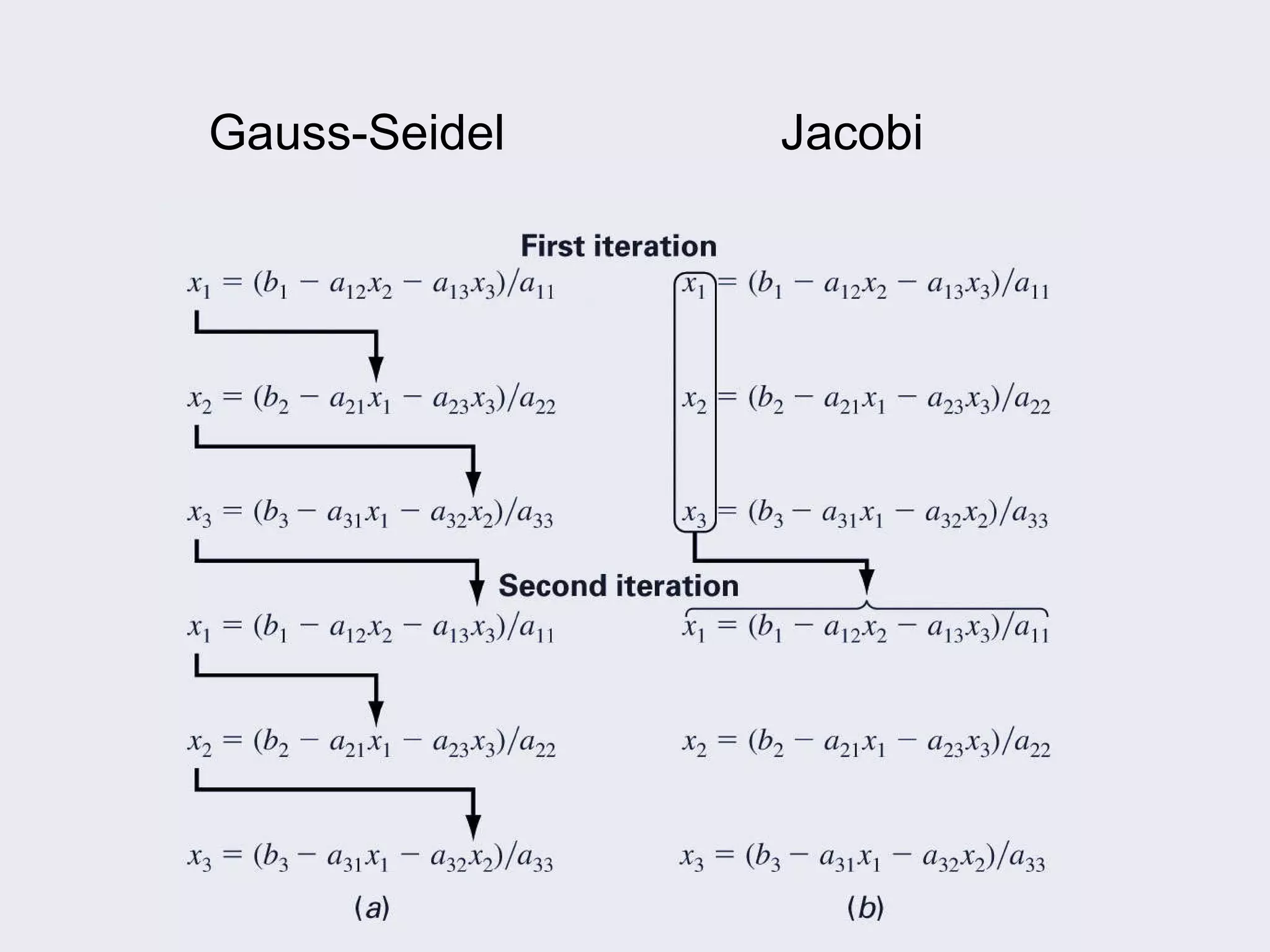
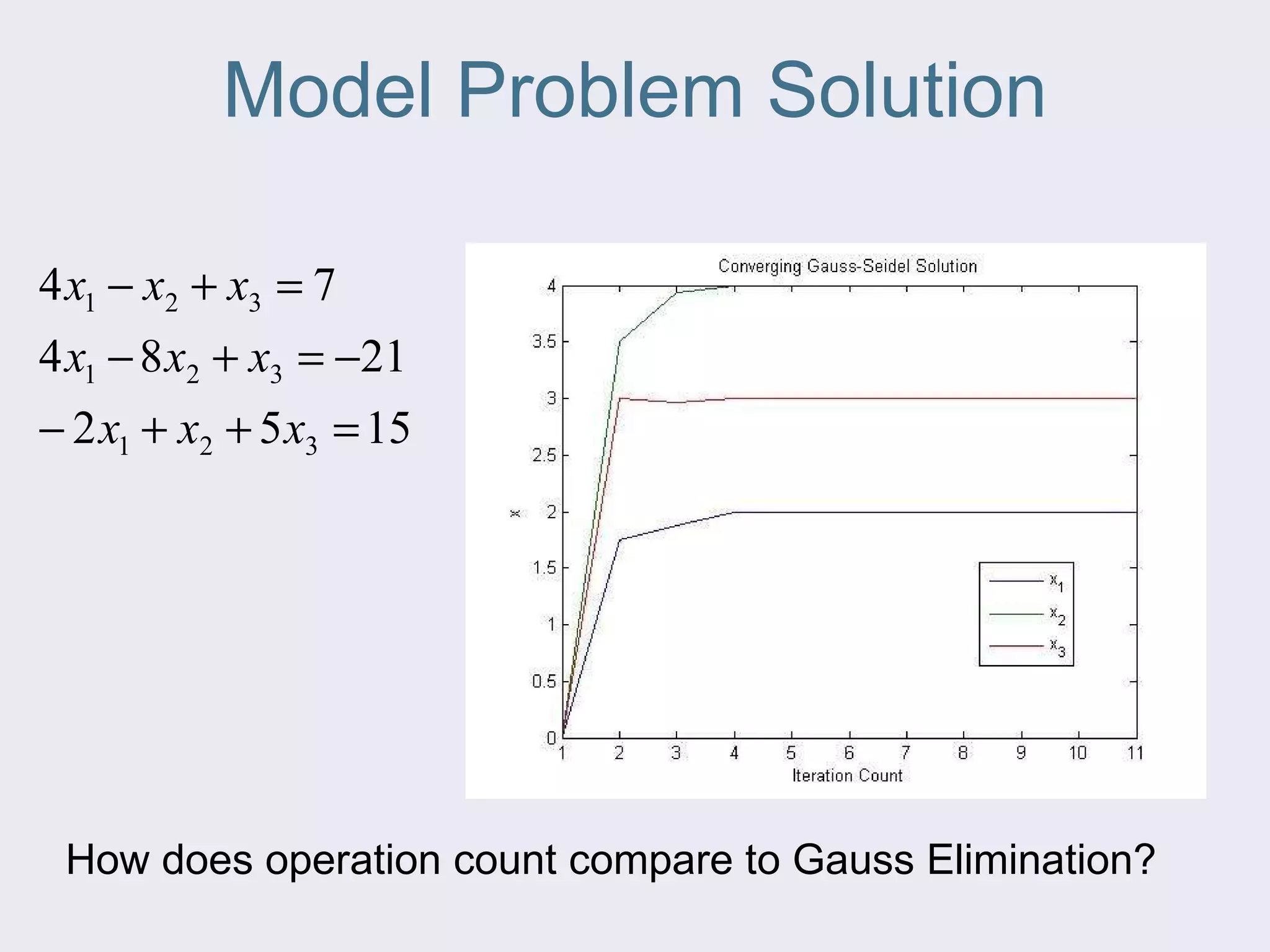
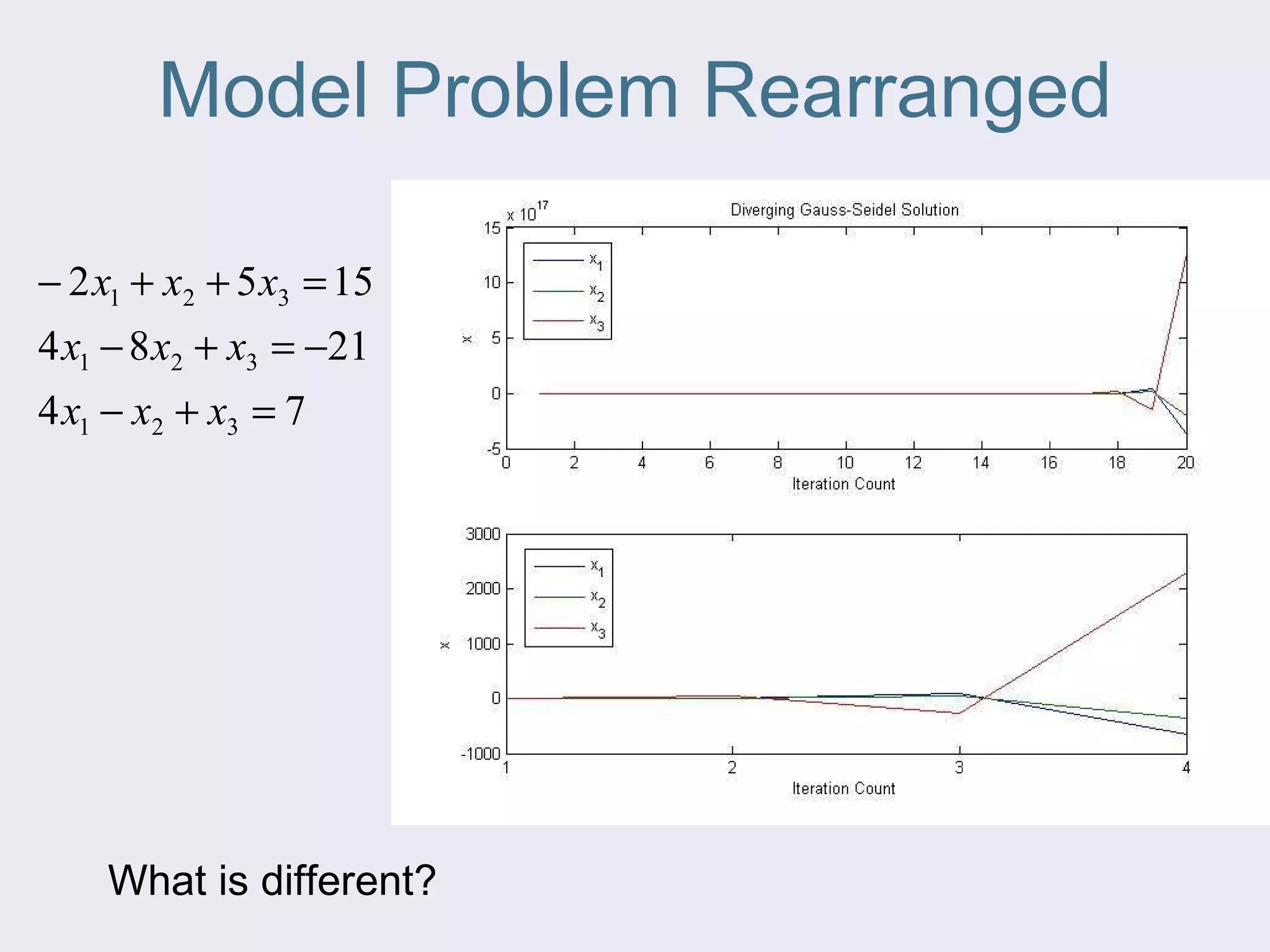
The document discusses several iterative methods for solving systems of equations, including Jacobi iteration, Gauss-Seidel method, and relaxation methods. The Gauss-Seidel method is commonly used and improves guesses for unknowns using values from the current iteration. Convergence is determined by calculating the relative percent change between iterations. Relaxation methods can enhance convergence by taking a weighted average of old and new values at each iteration.

1. Iterative Methods for Systems of Equations Linear Systems of Equations Jacobi Iteration Gauss-Seidel Convergence and diagonal dominance Relaxation Nonlinear Systems of Equations Newton-Raphson

2. Model Problem

3. Jacobi Iteration Algorithm Initial guesses Jacobi iteration Iterate until convergence criterion is met

4. Gauss-Seidel Method The Gauss-Seidel method is the most commonly used iterative method for solving linear algebraic equations Improve guesses for x 2 , x 3 , …, x n using the most recently calculated values from the present iteration Example iteration for 3x3 system:

5. Gauss-Seidel Jacobi

6. Convergence Convergence of an iterative method can be calculated by determining the relative percent change of each element in { x }. For example, for the i th element in the j th iteration, The method is ended when all elements have converged to a set tolerance.

7. Model Problem Solution How does operation count compare to Gauss Elimination?

8. Model Problem Rearranged What is different?

9. Diagonal Dominance The Gauss-Seidel method may diverge Diagonal dominance guarantees convergence, but is not necessary for convergence. Diagonal dominance means:

10. Relaxation Used to enhance convergence. Value at a particular iteration is made up of a combination of the old value and the newly calculated value: λ is a weighting factor that is assigned a value between 0 and 2. 0 < λ < 1: underrelaxation λ = 1: no relaxation 1 < λ ≤ 2: overrelaxation