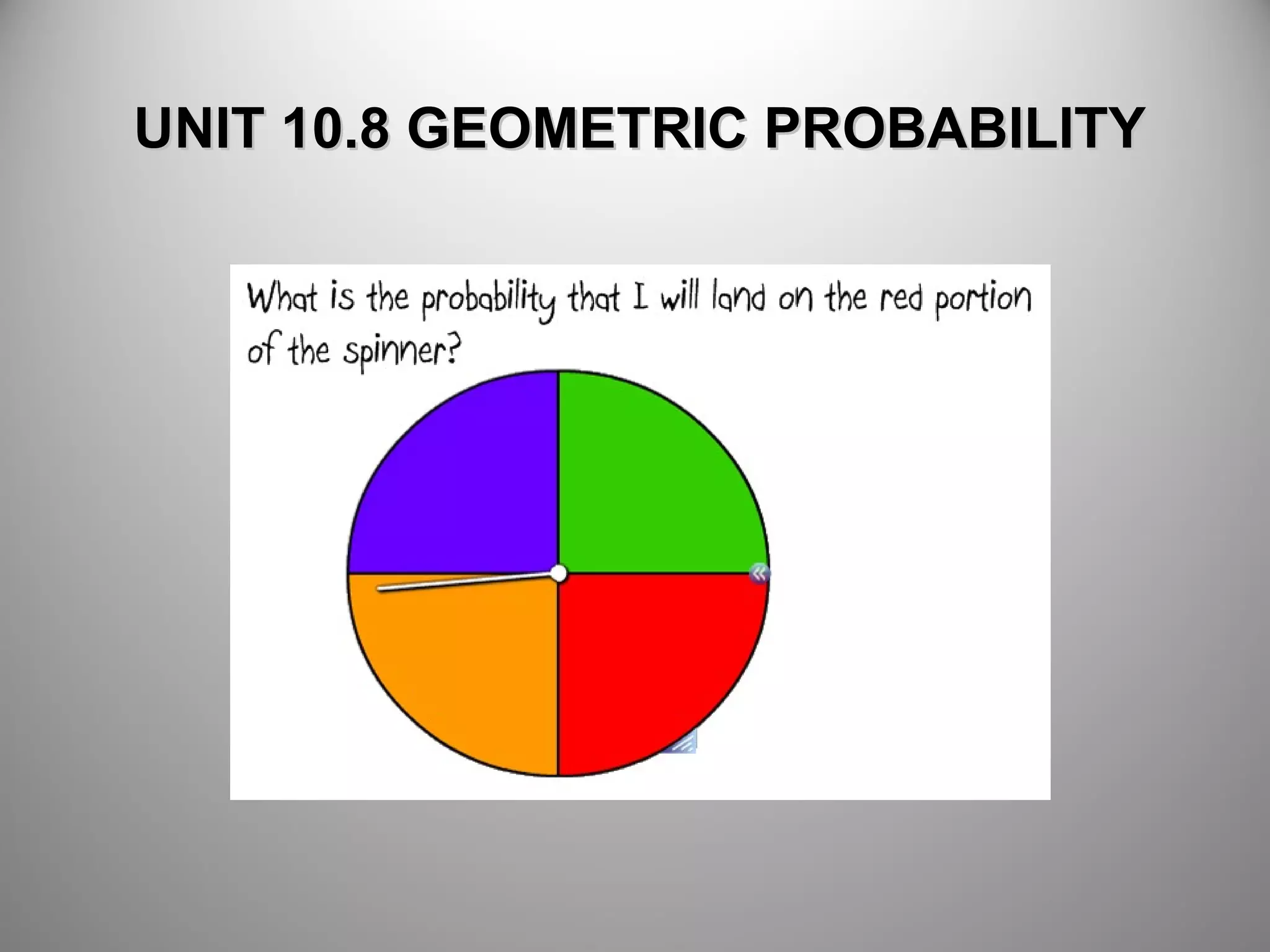
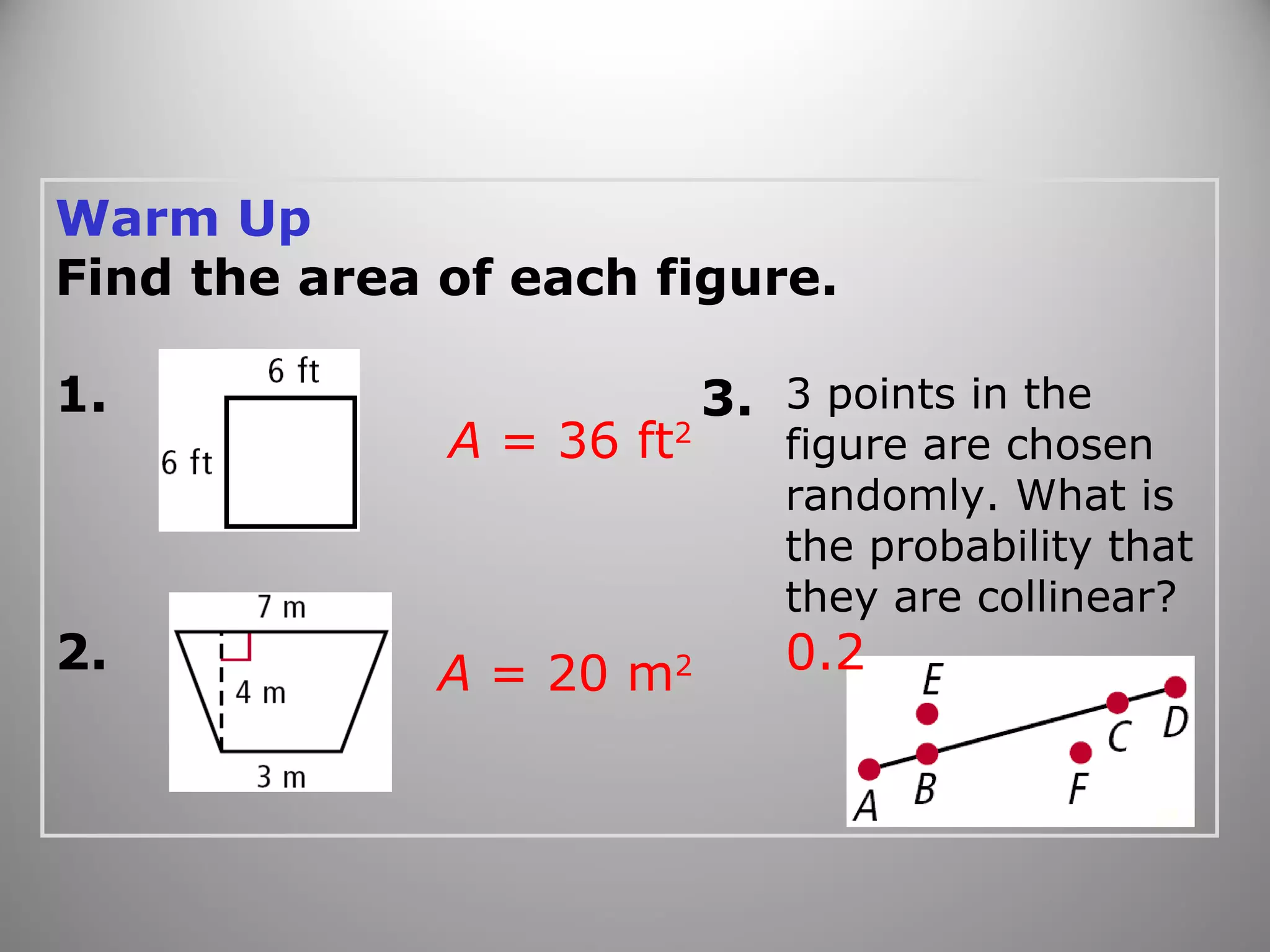
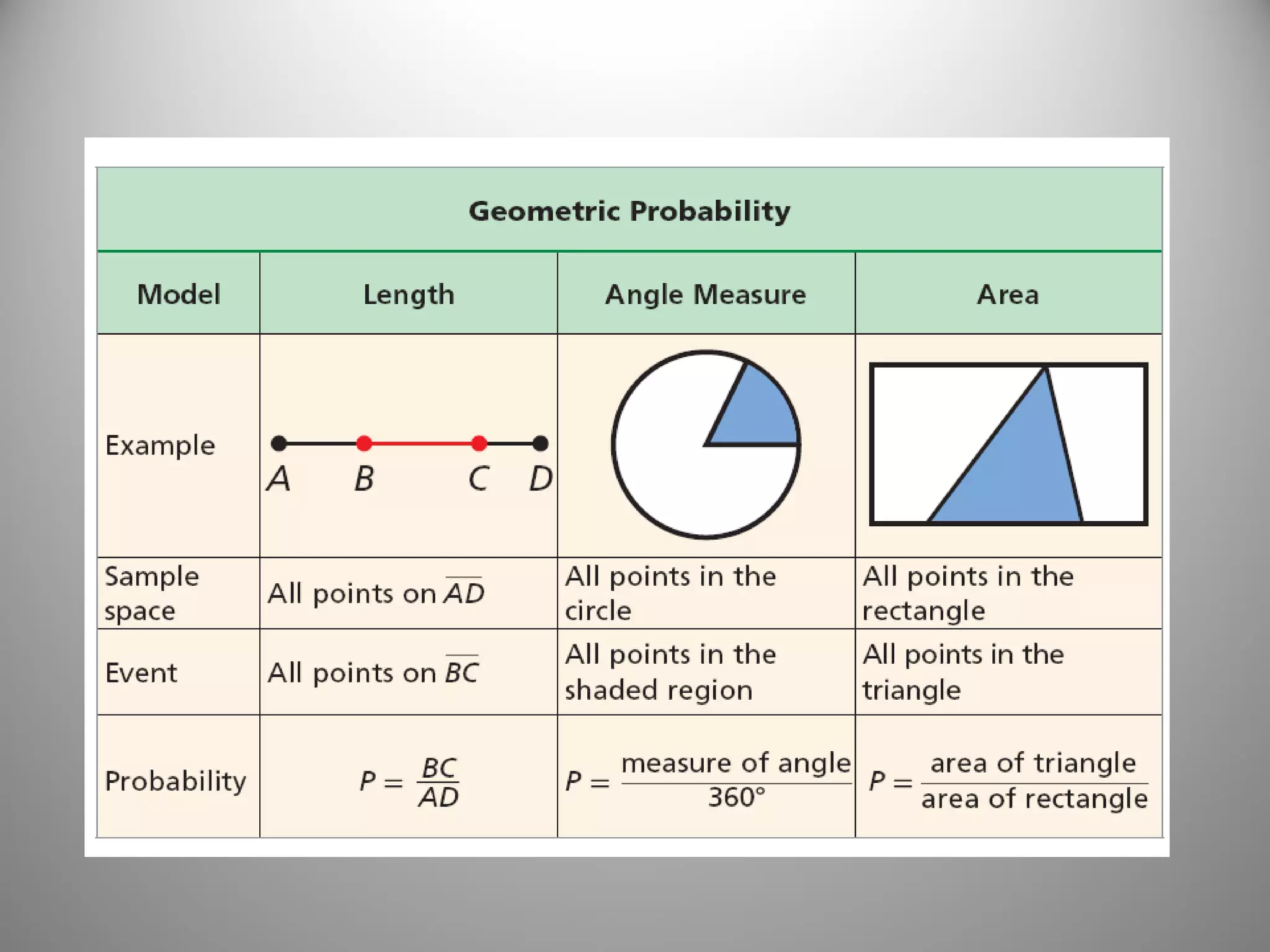
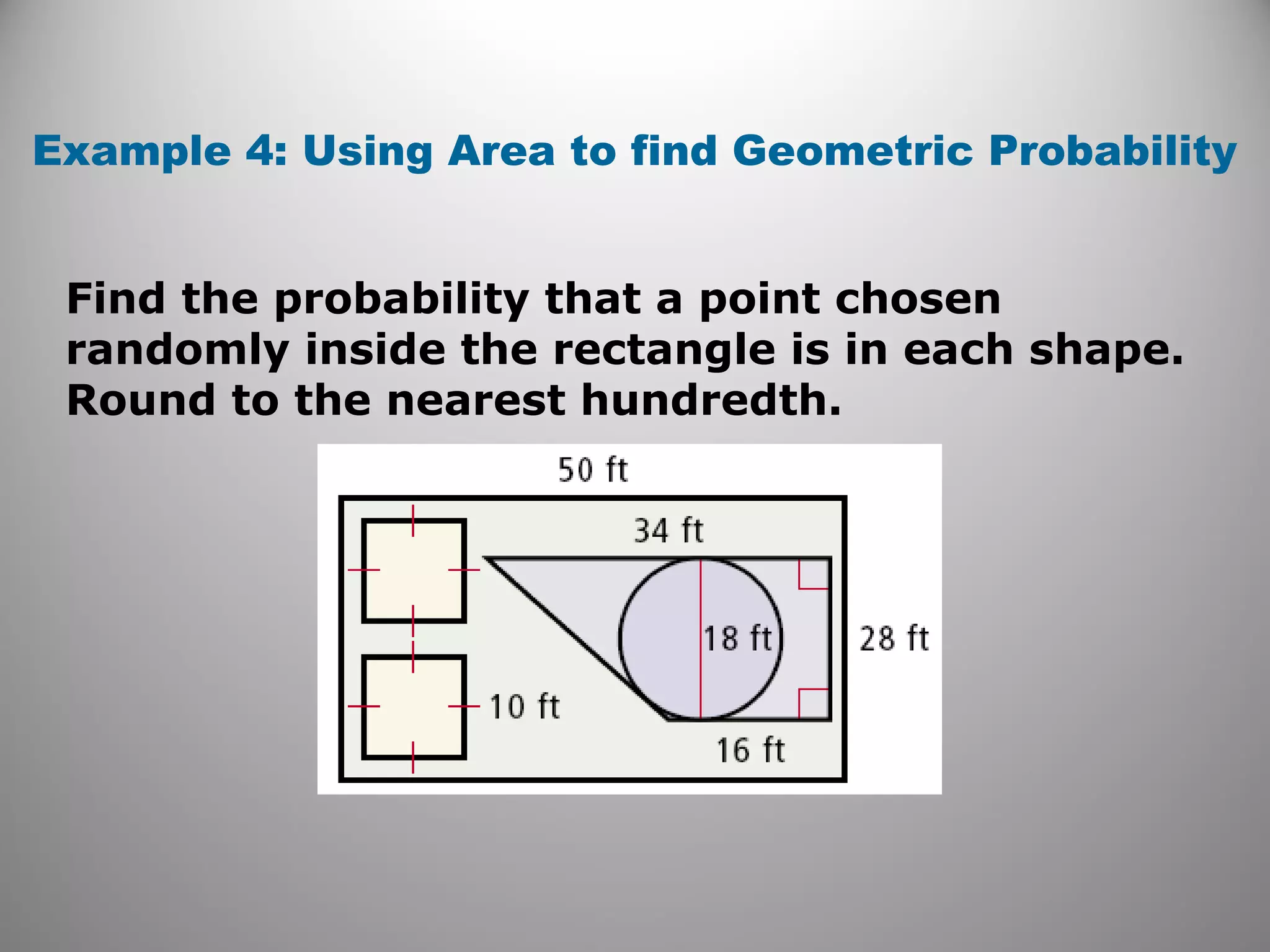
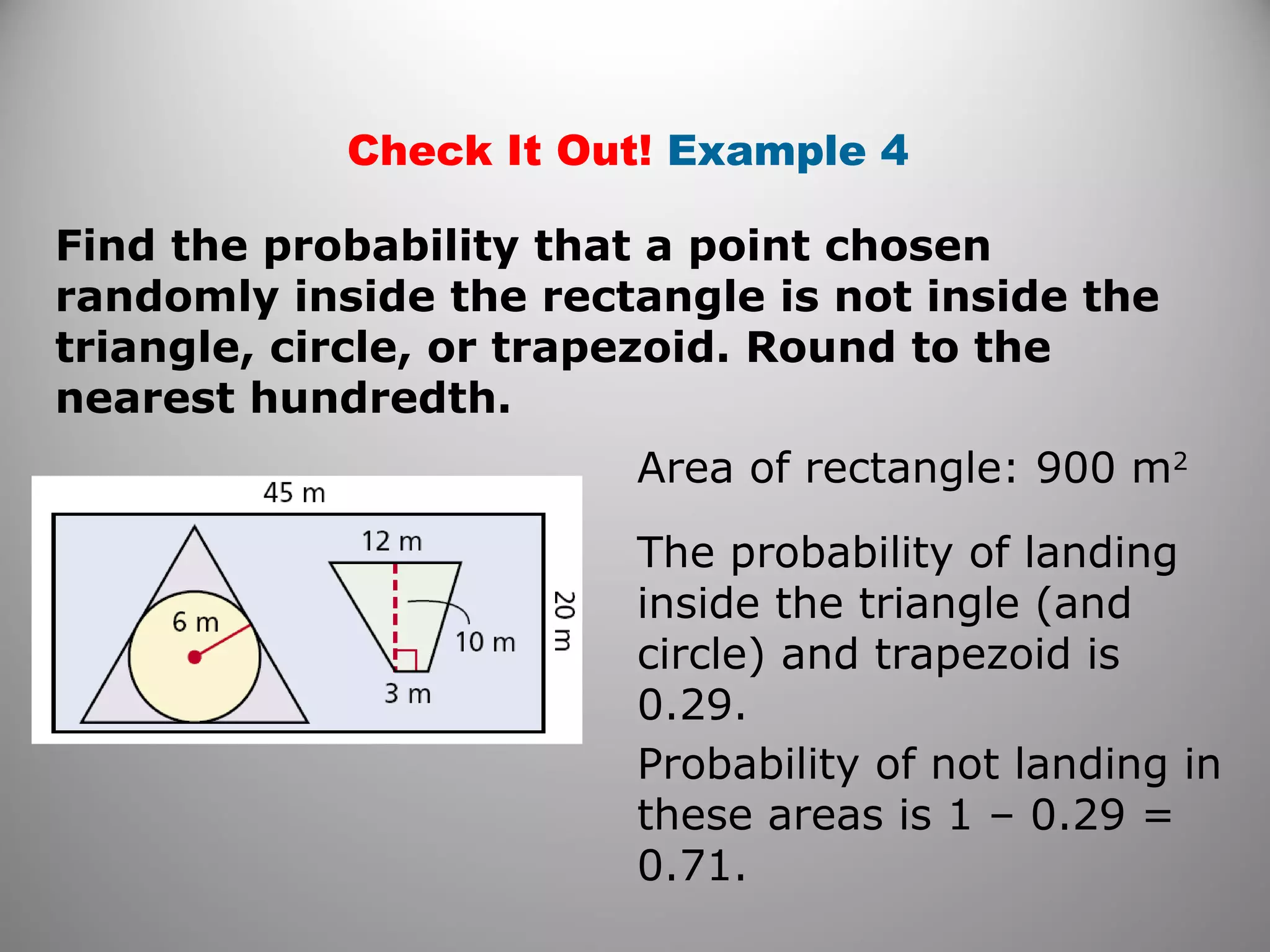
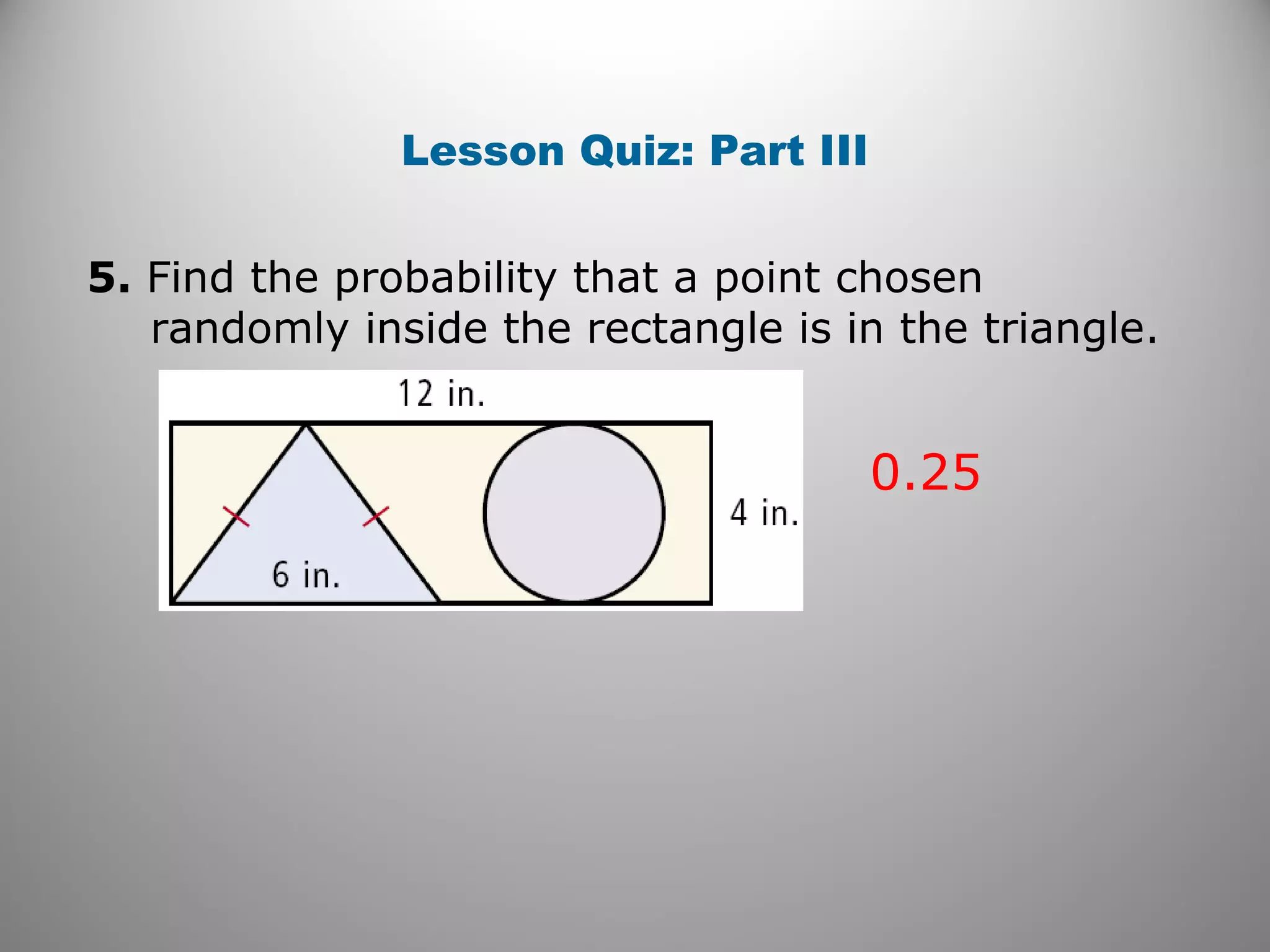
This document provides an overview of geometric probability and examples of calculating probabilities based on ratios of geometric measures like length, area, and angle measures. Geometric probability is used when an experiment has an infinite number of possible outcomes. Examples include finding the probability of a randomly selected point falling in a particular region of a line segment, shape, or spinner based on the relevant lengths, areas, or angle measures. The document also provides practice problems and solutions for calculating geometric probabilities.

1. UNIT 10.8 GEOMETRIC PROBABILITYUNIT 10.8 GEOMETRIC PROBABILITY

2. Warm Up
Find the area of each figure.
1.
A = 36 ft2
A = 20 m22.
3. 3 points in the
figure are chosen
randomly. What is
the probability that
they are collinear?
0.2

3. Calculate geometric probabilities.
Use geometric probability to predict
results in real-world situations.
Objectives

4. geometric probability
Vocabulary

5. Remember that in probability, the set of
all possible outcomes of an experiment
is called the sample space. Any set of
outcomes is called an event.
If every outcome in the sample space is
equally likely, the theoretical probability
of an event is

6. Geometric probability is used when an
experiment has an infinite number of
outcomes. In geometric probability,
the probability of an event is based on a
ratio of geometric measures such as
length or area. The outcomes of an
experiment may be points on a segment
or in a plane figure.

8. If an event has a probability p of occurring, the
probability of the event not occurring is 1 – p.
Remember!

9. A point is chosen randomly on PS. Find the
probability of each event.
Example 1A: Using Length to Find Geometric
Probability
The point is on RS.

10. Example 1B: Using Length to Find Geometric
Probability
The point is not on QR.
Subtract from 1 to find the probability that the
point is not on QR.

11. Example 1C: Using Length to Find Geometric
Probability
The point is on PQ or QR.
P(PQ or QR) = P(PQ) + P(QR)

12. Check It Out! Example 1
Use the figure below to find the probability
that the point is on BD.

13. A pedestrian signal at a crosswalk has the
following cycle: “WALK” for 45 seconds and
“DON’T WALK” for 70 seconds.
Example 2A: Transportation Application
What is the probability the signal will show
“WALK” when you arrive?
To find the probability, draw a segment to
represent the number of seconds that each signal
is on.
The signal is “WALK” for 45 out
of every 115 seconds.

14. Example 2B: Transportation Application
If you arrive at the signal 40 times, predict
about how many times you will have to stop
and wait more than 40 seconds.
In the model, the event of stopping and waiting
more than 40 seconds is represented by a segment
that starts at B and ends 40 units from C. The
probability of stopping and waiting more than 40
seconds is
If you arrive at the light 40 times, you will probably
stop and wait more than 40 seconds about
(40) ≈ 10 times.

15. Check It Out! Example 2
Use the information below. What is the
probability that the light will not be on red
when you arrive?
The probability that the light will be on red is

16. Use the spinner to find the probability of each
event.
Example 3A: Using Angle Measures to Find
Geometric Probability
the pointer landing on yellow
The angle measure in the
yellow region is 140°.

17. Example 3B: Using Angle Measures to Find
Geometric Probability
the pointer landing on blue or red
The angle measure in the blue region is 52°.
The angle measure in the red region is 60°.
Use the spinner to find the probability of each
event.

18. Example 3C: Using Angle Measures to Find
Geometric Probability
the pointer not landing on green
The angle measure in the green region is 108°.
Subtract this angle measure from 360°.
Use the spinner to find the probability of each
event.

19. Check It Out! Example 3
Use the spinner below to find the probability
of the pointer landing on red or yellow.
The probability is that the
spinner will land on red or
yellow.

20. Find the probability that a point chosen
randomly inside the rectangle is in each shape.
Round to the nearest hundredth.
Example 4: Using Area to find Geometric Probability

21. Example 4A: Using Area to find Geometric Probability
the circle
The area of the circle is A = πr2
= π(9)2
= 81π ≈ 254.5 ft2
.
The area of the rectangle is A = bh
= 50(28) = 1400 ft2
.
The probability is P =
254.5
1400
≈ 0.18.

22. Example 4B: Using Area to find Geometric Probability
the trapezoid
The area of the rectangle is A = bh
= 50(28) = 1400 ft2
.
The area of the trapezoid is
The probability is

23. Example 4C: Using Area to find Geometric Probability
one of the two squares
The area of the two squares is A = 2s2
= 2(10)2
= 200 ft2
.
The area of the rectangle is A = bh
= 50(28) = 1400 ft2
.
The probability is

24. Check It Out! Example 4
Area of rectangle: 900 m2
Find the probability that a point chosen
randomly inside the rectangle is not inside the
triangle, circle, or trapezoid. Round to the
nearest hundredth.
The probability of landing
inside the triangle (and
circle) and trapezoid is
0.29.
Probability of not landing in
these areas is 1 – 0.29 =
0.71.

25. Lesson Quiz: Part I
A point is chosen randomly on EH. Find the
probability of each event.
1. The point is on EG.
2. The point is not on EF.
3
5
13
15

26. Lesson Quiz: Part II
3. An antivirus program has the following cycle:
scan: 15 min, display results: 5 min, sleep: 40
min. Find the probability that the program will
be scanning when you arrive at the computer.
0.25
4. Use the spinner to find the probability of the
pointer landing on a shaded area.
0.5

27. Lesson Quiz: Part III
5. Find the probability that a point chosen
randomly inside the rectangle is in the triangle.
0.25

28.
All rights belong to their respective owners.
Copyright Disclaimer Under Section 107 of
the Copyright Act 1976, allowance is made
for "fair use" for purposes such as criticism,
comment, news reporting, TEACHING,
scholarship, and research.
Fair use is a use permitted by copyright
statute that might otherwise be infringing.
Non-profit, EDUCATIONAL or personal use
tips the balance in favor of fair use.