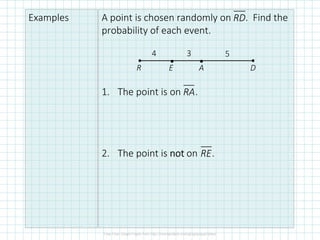
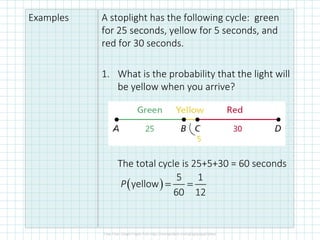
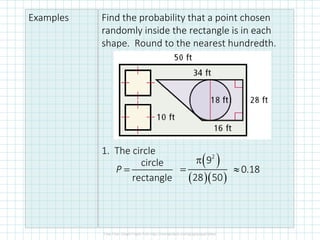
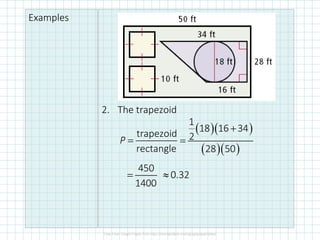
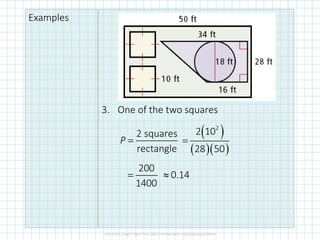
The student understands: 1) How to calculate probabilities using geometric measures like lengths and areas of shapes. 2) How to use geometric probability to predict outcomes in real-world situations like traffic lights and spinners. 3) How to find the probability of events occurring individually or jointly using addition and multiplication of probabilities.

1. Geometric Probability
The student is able to (I can):
• Calculate geometric probabilites
• Use geometric probability to predict results in real-world
situations

2. sample spacesample spacesample spacesample space – the set of all possible outcomes for the event
theoretical probabilitytheoretical probabilitytheoretical probabilitytheoretical probability – if every outcome in a sample space is
equally likely to occur, then the theoretical
probability of an event is
experimental probabilityexperimental probabilityexperimental probabilityexperimental probability – is based on repeated trials of a
probability experiment. Each trial in which a
favorable outcome occurs is called a success. The
experimental probability can be found by
number of outcomes in the event
number of outcomes in the sample space
=P
number of successes
number of trials
P =

3. geometric probabilitygeometric probabilitygeometric probabilitygeometric probability – the probability of an event is based
on a ratio of geometric measures such as length or
area. The outcomes of an experiment may be points
on a segment or in a plane figure.
The probability of an event’s notnotnotnot happening is
1 – the probability of the event’s happening.

4. Examples A point is chosen randomly on . Find the
probability of each event.
1. The point is on .
2. The point is notnotnotnot on .
RD
••
DAER
4 3 5
RA
RE

5. Examples A point is chosen randomly on . Find the
probability of each event.
1. The point is on .
2. The point is notnotnotnot on .
RD
••
DAER
4 3 5
RA
( ) RA
P RA
RD
=
7
12
=
RE
( ) ( )not 1P RE P RE= − 1
RE
RD
= −
4 8 2
1
12 12 3
= − = =

6. Examples A stoplight has the following cycle: green
for 25 seconds, yellow for 5 seconds, and
red for 30 seconds.
1. What is the probability that the light will
be yellow when you arrive?
The total cycle is 25+5+30 = 60 seconds
( )
5 1
yellow
60 12
P = =

7. Examples
2. If you arrive at the light 50 times,
predict about how many times you will
have to wait more than 10 seconds.
Therefore, if you arrive at the light 50
times, you will probably stop and wait
more than 10 seconds about
•
10E20
20 1
60 3
CE
P
AD
= = =
( )
1
50 17 times
3
≈

8. Examples Use the spinner to find the probability of
each event.
1. Landing on red
2. Landing on purple or blue
3. Not landing on yellow
80 2
360 9
P = =
75 60
360
P
+
=
135
360
=
3
8
=
100 360 100
1
360 360
P
−
= − =
260 13
360 18
= =

9. Examples Find the probability that a point chosen
randomly inside the rectangle is in each
shape. Round to the nearest hundredth.
1. The circle
circle
rectangle
P =
( )
( )( )
2
9
28 50
π
= 0.18≈

10. Examples
2. The trapezoid
trapezoid
rectangle
P =
( )( )
( )( )
1
18 16 34
2
28 50
+
=
450
1400
= 0.32≈

11. Examples
3. One of the two squares
2 squares
rectangle
=P
( )
( )( )
2
2 10
28 50
=
200
1400
= 0.14≈

12. compound
probability
The probability of two or more events in
the same sample space.
Event #1 OR Event #2 Add the
probabilities
Event #1 AND Event #2 Multiply the
probabilities