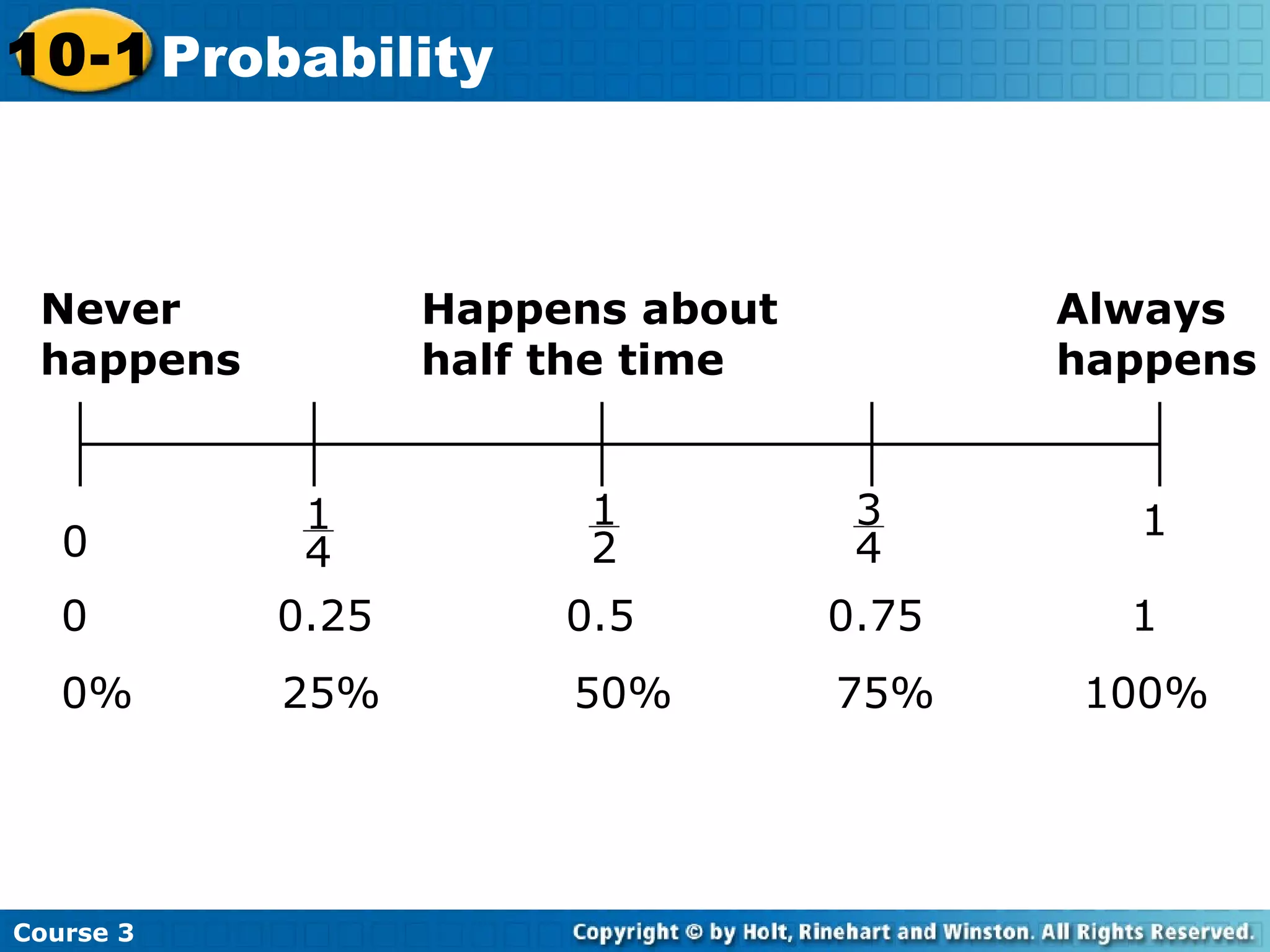
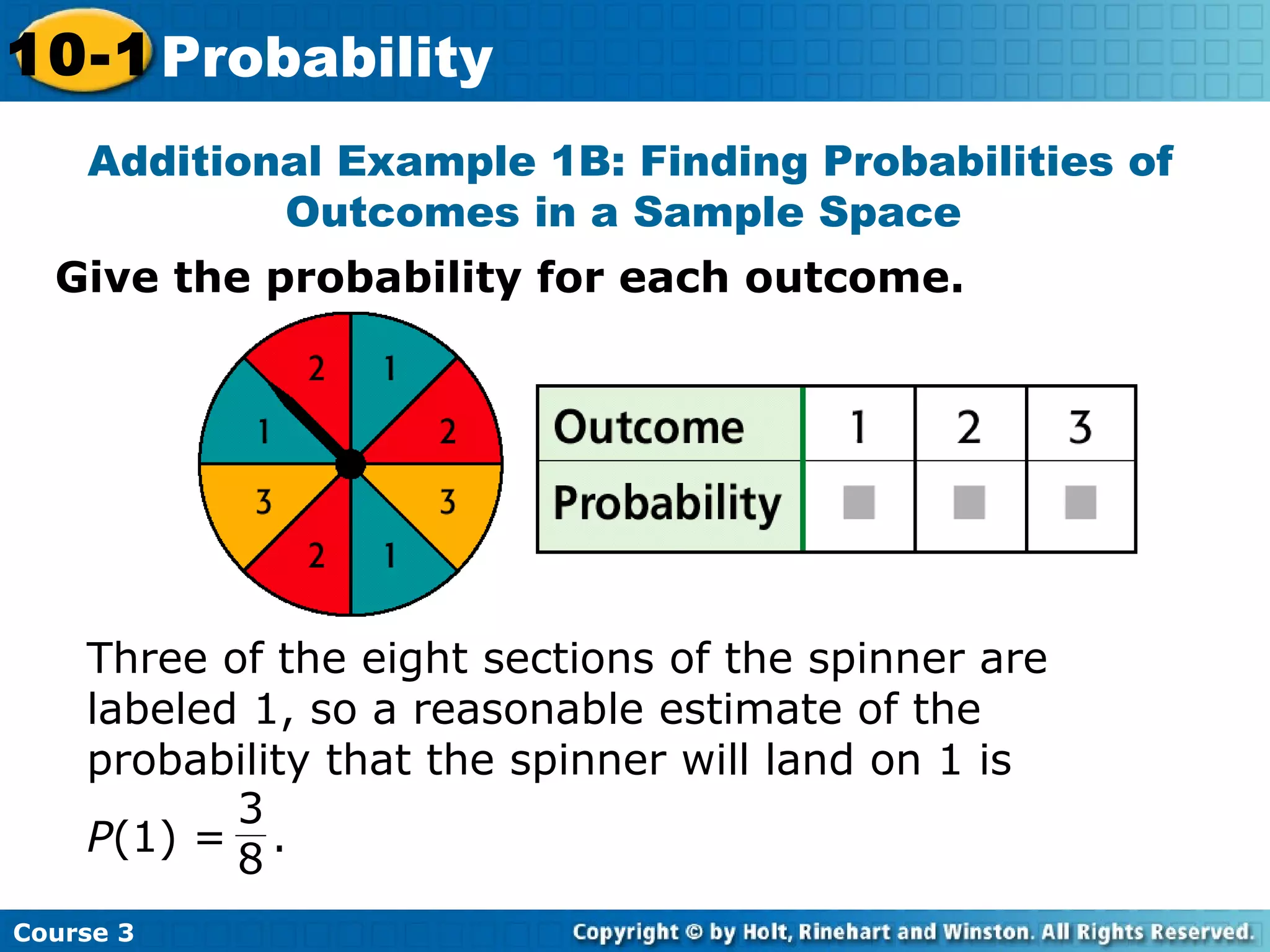
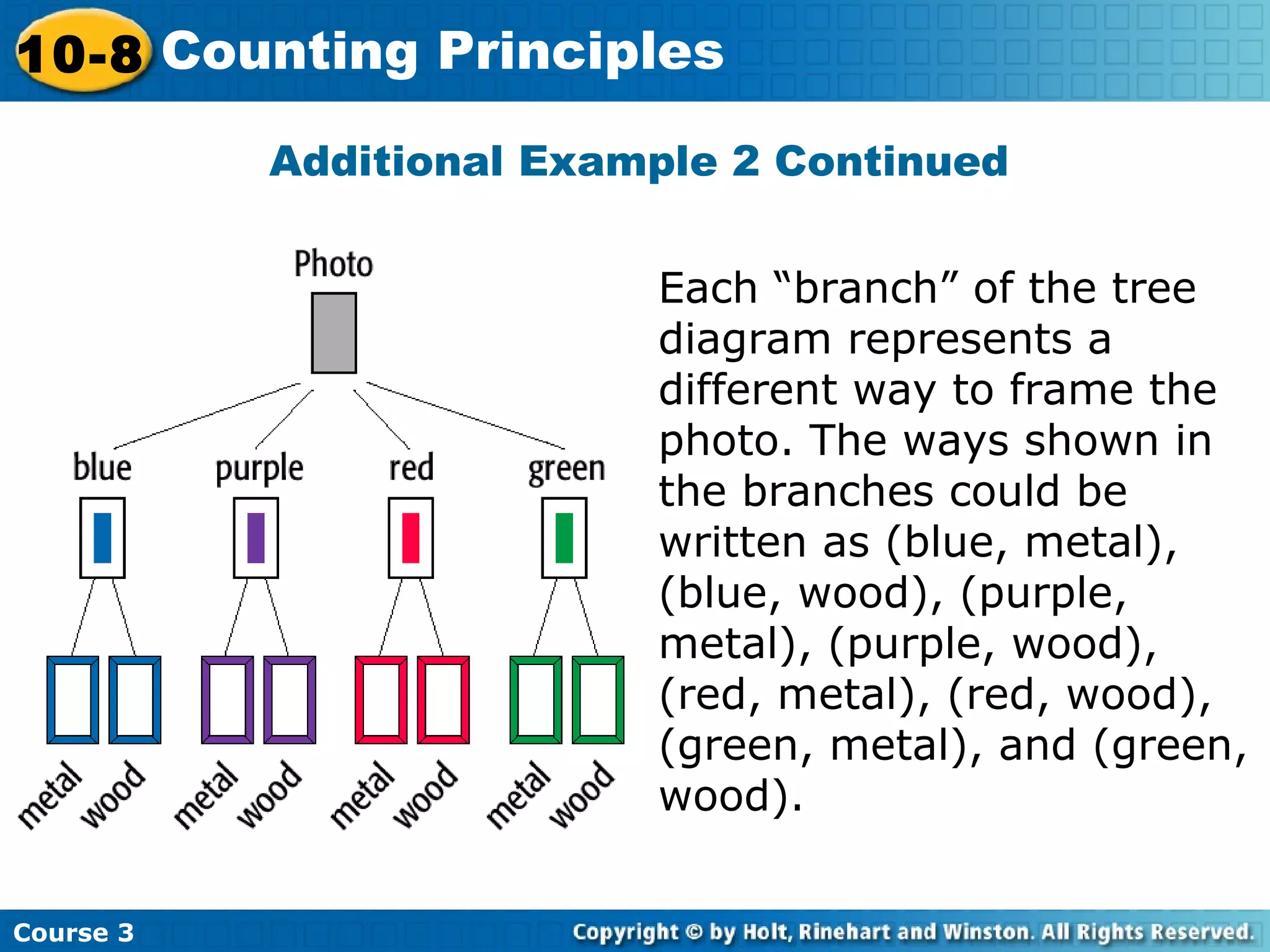
This document covers probability concepts including experiments, outcomes, sample spaces, events, and probabilities. It defines key terms and provides examples of calculating probabilities of outcomes and events using concepts like the fundamental counting principle and determining if events are independent or dependent. Sample problems are given throughout for practicing these probability concepts and determining the number of possible outcomes, finding individual outcome probabilities, and calculating probabilities of compound events.

1. Various Probability Concepts

2. Learn to find the probability of an event
by using the definition of probability.
Course 3
10-1 Probability

3. Vocabulary
experiment
trial
outcome
sample space
event
probability
impossible
certain
Insert Lesson Title Here
Course 3
10-1 Probability

4. Course 3
10-1 Probability
An experiment is an activity in which results
are observed. Each observation is called a trial,
and each result is called an outcome. The
sample space is the set of all possible
outcomes of an experiment.
Experiment Sample Space
flipping a coin heads, tails
rolling a number cube 1, 2, 3, 4, 5, 6
guessing the number of whole numbers
marbles in a jar

5. Course 3
10-1 Probability
An event is any set of one or more outcomes.
The probability of an event, written P(event),
is a number from 0 (or 0%) to 1 (or 100%) that
tells you how likely the event is to happen.
• A probability of 0 means the event is
impossible, or can never happen.
• A probability of 1 means the event is certain,
or has to happen.
• The probabilities of all the outcomes in the
sample space add up to 1.

6. Course 3
10-1 Probability
0 0.25 0.5 0.75 1
0% 25% 50% 75% 100%
Never Happens about Always
happens half the time happens
1
4
1
2
3
40
1

7. Give the probability for each outcome.
Additional Example 1A: Finding Probabilities of
Outcomes in a Sample Space
Course 3
10-1 Probability
The basketball team has a
70% chance of winning.
The probability of winning is P(win) = 70% =
0.7. The probabilities must add to 1, so the
probability of not winning is P(lose) = 1 – 0.7 =
0.3, or 30%.

8. Give the probability for each outcome.
Additional Example 1B: Finding Probabilities of
Outcomes in a Sample Space
Course 3
10-1 Probability
Three of the eight sections of the spinner are
labeled 1, so a reasonable estimate of the
probability that the spinner will land on 1 is
P(1) = .
3
8

9. Additional Example 1B Continued
Course 3
10-1 Probability
Three of the eight sections of the spinner are
labeled 2, so a reasonable estimate of the
probability that the spinner will land on 2 is
P(2) = .3
8
Two of the eight sections of the spinner are
labeled 3, so a reasonable estimate of the
probability that the spinner will land on 3 is
P(3) = = .2
8
1
4
Check The probabilities of all the outcomes
must add to 1.
3
8
3
8
2
8
++ = 1

10. Give the probability for each outcome.
Check It Out: Example 1A
Course 3
10-1 Probability
The polo team has a
50% chance of
winning.
The probability of winning is P(win) = 50% = 0.5.
The probabilities must add to 1, so the probability
of not winning is P(lose) = 1 – 0.5 = 0.5, or 50%.

11. Give the probability for each outcome.
Check It Out: Example 1B
Course 3
10-1 Probability
Rolling a
number cube.
One of the six sides of a cube is labeled 1, so
a reasonable estimate of the probability that the
spinner will land on 1 is P(1) = . 1
6
Outcome 1 2 3 4 5 6
Probability
One of the six sides of a cube is labeled 2, so
a reasonable estimate of the probability that the
spinner will land on 2 is P(2) = . 1
6

12. Check It Out: Example 1B Continued
Course 3
10-1 Probability
One of the six sides of a cube is labeled 3, so
a reasonable estimate of the probability that the
spinner will land on 3 is P(3) = . 1
6
One of the six sides of a cube is labeled 4, so
a reasonable estimate of the probability that the
spinner will land on 4 is P(4) = . 1
6
One of the six sides of a cube is labeled 5, so
a reasonable estimate of the probability that the
spinner will land on 5 is P(5) = . 1
6

13. Check It Out: Example 1B Continued
Course 3
10-1 Probability
One of the six sides of a cube is labeled 6, so
a reasonable estimate of the probability that the
spinner will land on 6 is P(6) = . 1
6
Check The probabilities of all the outcomes
must add to 1.

1
6
1
6
1
6
++ = 1
1
6
+
1
6
+
1
6
+

14. Course 3
10-1 Probability
To find the probability of an event, add the
probabilities of all the outcomes included in the
event.

15. Learn to find the number of possible
outcomes in an experiment.
Course 3
10-8 Counting Principles

16. Vocabulary
Fundamental Counting Principle
tree diagram
Addition Counting Principle
Insert Lesson Title Here
Course 3
10-8 Counting Principles

17. Course 3
10-8 Counting Principles

18. License plates are being produced that have a
single letter followed by three digits. All
license plates are equally likely.
Additional Example 1A: Using the Fundamental
Counting Principle
Find the number of possible license plates.
Use the Fundamental Counting Principal.
letter first digit second digit third digit
26 choices 10 choices 10 choices 10 choices
26 • 10 • 10 • 10 = 26,000
The number of possible 1-letter, 3-digit license
plates is 26,000.
Course 3
10-8 Counting Principles

19. Additional Example 1B: Using the Fundamental
Counting Principal
Find the probability that a license plate
has the letter Q.
1 • 10 • 10 • 10
26,000 =
1
26
≈ 0.038P(Q ) =
Course 3
10-8 Counting Principles

20. Additional Example 1C: Using the Fundamental
Counting Principle
Find the probability that a license plate does not
contain a 3.
First use the Fundamental Counting Principle to
find the number of license plates that do not
contain a 3.
26 • 9 • 9 • 9 = 18,954 possible license plates
without
a 3There are 9 choices for any
digit except 3.
P(no 3) = = 0.729
26,000
18,954
Course 3
10-8 Counting Principles

21. Social Security numbers contain 9 digits. All
social security numbers are equally likely.
Check It Out: Example 1A
Find the number of possible Social Security
numbers.
Use the Fundamental Counting Principle.
Digit 1 2 3 4 5 6 7 8 9
Choices 10 10 10 10 10 10 10 10 10
10 • 10 • 10 • 10 • 10 • 10 • 10 • 10 • 10 =
1,000,000,000
The number of Social Security numbers is
1,000,000,000.
Course 3
10-8 Counting Principles

22. Check It Out: Example 1B
Find the probability that the Social Security
number contains a 7.
P(7 _ _ _ _ _ _ _ _) = 1 • 10 • 10 • 10 • 10 • 10 • 10 • 10 • 10
1,000,000,000
= = 0.1
10
1
Course 3
10-8 Counting Principles

23. Check It Out: Example 1C
Find the probability that a Social Security
number does not contain a 7.
First use the Fundamental Counting Principle to find
the number of Social Security numbers that do not
contain a 7.
P(no 7 _ _ _ _ _ _ _ _) = 9 • 9 • 9 • 9 • 9 • 9 • 9 • 9 • 9
1,000,000,000
P(no 7) = ≈ 0.4
1,000,000,000
387,420,489
Course 3
10-8 Counting Principles

24. The Fundamental Counting Principle tells you
only the number of outcomes in some
experiments, not what the outcomes are. A tree
diagram is a way to show all of the possible
outcomes.
Course 3
10-8 Counting Principles

25. Additional Example 2: Using a Tree Diagram
You have a photo that you want to mat and
frame. You can choose from a blue, purple, red,
or green mat and a metal or wood frame.
Describe all of the ways you could frame this
photo with one mat and one frame.
You can find all of the possible outcomes by
making a tree diagram.
There should be 4 • 2 = 8 different ways to
frame the photo.
Course 3
10-8 Counting Principles

26. Additional Example 2 Continued
Each “branch” of the tree
diagram represents a
different way to frame the
photo. The ways shown in
the branches could be
written as (blue, metal),
(blue, wood), (purple,
metal), (purple, wood),
(red, metal), (red, wood),
(green, metal), and (green,
wood).
Course 3
10-8 Counting Principles

27. Check It Out: Example 2
A baker can make yellow or white cakes
with a choice of chocolate, strawberry, or
vanilla icing. Describe all of the possible
combinations of cakes.
You can find all of the possible outcomes by
making a tree diagram.
There should be 2 • 3 = 6 different cakes
available.
Course 3
10-8 Counting Principles

28. Check It Out: Example 2 Continued
The different cake
possibilities are
(yellow, chocolate),
(yellow, strawberry),
(yellow, vanilla),
(white, chocolate),
(white, strawberry),
and (white, vanilla).
white cake
yellow cake
chocolate
icing
vanilla icing
strawberry
icing
chocolate
icing
vanilla icing
strawberry
icing
Course 3
10-8 Counting Principles

29. Additional Example 3: Using the Addition Counting
Principle
The table shows the items available at a farm
stand. How many items can you choose from
the farm stand?
None of the lists contains identical items, so use
the Addition Counting Principle.
Total Choices
Course 3
10-8 Counting Principles
Apples Pears Squash+= +
Apples Pears Squash
Macintosh Bosc Acorn
Red Delicious Yellow Bartlett Hubbard
Gold Delicious Red Bartlett

30. Additional Example 3 Continued
Course 3
10-8 Counting Principles
T 3 3 2+= + = 8
There are 8 items to choose from.

31. Learn to find the probabilities of
independent and dependent events.
Course 3
10-5
Independent and
Dependent Events

32. Vocabulary
compound events
independent events
dependent events
Insert Lesson Title Here
Course 3
10-5
Independent and
Dependent Events

33. A compound event is made up of one or
more separate events. To find the probability
of a compound event, you need to know if
the events are independent or dependent.
Course 3
10-5
Independent and
Dependent Events
Events are independent events if the
occurrence of one event does not affect the
probability of the other. Events are
dependent events if the occurrence of one
does affect the probability of the other.

34. Determine if the events are dependent or
independent.
A. getting tails on a coin toss and rolling a 6
on a number cube
B. getting 2 red gumballs out of a gumball
machine
Additional Example 1: Classifying Events as
Independent or Dependent
Tossing a coin does not affect rolling a number
cube, so the two events are independent.
After getting one red gumball out of a gumball
machine, the chances for getting the second red
gumball have changed, so the two events are
dependent.
Course 3
10-5
Independent and
Dependent Events

35. Determine if the events are dependent or
independent.
A. rolling a 6 two times in a row with the same
number cube
B. a computer randomly generating two of the
same numbers in a row
Check It Out: Example 1
The first roll of the number cube does not affect
the second roll, so the events are independent.
The first randomly generated number does not
affect the second randomly generated number, so
the two events are independent.
Course 3
10-5
Independent and
Dependent Events

36. Course 3
10-5
Independent and
Dependent Events

37. Three separate boxes each have one blue
marble and one green marble. One marble is
chosen from each box.
What is the probability of choosing a blue
marble from each box?
Additional Example 2A: Finding the Probability of
Independent Events
The outcome of each choice does not affect the
outcome of the other choices, so the choices are
independent.
P(blue, blue, blue) =
In each box, P(blue) = .
1
2
1
2
· 1
2
· 1
2
=
1
8
= 0.125 Multiply.
Course 3
10-5
Independent and
Dependent Events

38. What is the probability of choosing at least
one blue marble?
Additional Example 2C: Finding the Probability of
Independent Events
1 – 0.125 = 0.875
Subtract from 1 to find the probability of
choosing at least one blue marble.
Think: P(at least one blue) + P(not blue,
not blue, not blue) = 1.
In each box, P(not blue) = .
1
2P(not blue, not blue, not blue) =
1
2
· 1
2
· 1
2
= 1
8
= 0.125 Multiply.
Course 3
10-5
Independent and
Dependent Events

39. Two boxes each contain 4 marbles: red, blue,
green, and black. One marble is chosen from
each box.
What is the probability of choosing a blue
marble from each box?
Check It Out: Example 2A
The outcome of each choice does not affect the
outcome of the other choices, so the choices are
independent.
In each box, P(blue) = .
1
4
P(blue, blue) =
1
4
· 1
4
=
1
16
= 0.0625 Multiply.
Course 3
10-5
Independent and
Dependent Events

40. Two boxes each contain 4 marbles: red, blue,
green, and black. One marble is chosen from
each box.
What is the probability of choosing a blue marble
and then a red marble?
Check It Out: Example 2B
In each box, P(blue) = .
1
4
P(blue, red) =
1
4
· 1
4
=
1
16
= 0.0625 Multiply.
In each box, P(red) = .
1
4
Course 3
10-5
Independent and
Dependent Events

41. Two boxes each contain 4 marbles: red, blue,
green, and black. One marble is chosen from
each box.
What is the probability of choosing at least one
blue marble?
Check It Out: Example 2C
In each box, P(blue) = .
1
4
P(not blue, not blue) =
3
4
· 3
4
=
9
16
= 0.5625 Multiply.
Think: P(at least one blue) + P(not blue,
not blue) = 1.
1 – 0.5625 = 0.4375
Subtract from 1 to find the probability of choosing at
least one blue marble.
Course 3
10-5
Independent and
Dependent Events

42. Course 3
10-5
Independent and
Dependent Events
To calculate the probability of two dependent
events occurring, do the following:
1. Calculate the probability of the first event.
2. Calculate the probability that the second
event would occur if the first event had
already occurred.
3. Multiply the probabilities.

43. The letters in the word dependent are placed
in a box.
If two letters are chosen at random, what is
the probability that they will both be
consonants?
Additional Example 3A: Find the Probability of
Dependent Events
P(first consonant) =
Course 3
10-5
Independent and
Dependent Events
2
3
6
9
=
Because the first letter is not replaced, the sample
space is different for the second letter, so the
events are dependent. Find the probability that the
first letter chosen is a consonant.

44. Additional Example 3A Continued
Course 3
10-5
Independent and
Dependent Events
If the first letter chosen was a consonant, now
there would be 5 consonants and a total of 8 letters
left in the box. Find the probability that the second
letter chosen is a consonant.
P(second consonant) =
5
8
5
12
5
8
2
3
· =
The probability of choosing two letters that are
both consonants is .
5
12
Multiply.

45. If two letters are chosen at random, what is
the probability that they will both be
consonants or both be vowels?
Additional Example 3B: Find the Probability of
Dependent Events
There are two possibilities: 2 consonants or 2
vowels. The probability of 2 consonants was
calculated in Example 3A. Now find the probability
of getting 2 vowels.
Find the probability that
the first letter chosen is a
vowel.
If the first letter chosen was a vowel, there are now
only 2 vowels and 8 total letters left in the box.
Course 3
10-5
Independent and
Dependent Events
P(first vowel) =
1
3
3
9
=

46. Additional Example 3B Continued
Find the probability that
the second letter chosen is
a vowel.
The events of both consonants and both vowels are
mutually exclusive, so you can add their probabilities.
Course 3
10-5
Independent and
Dependent Events
P(second vowel) =
1
4
2
8
=
1
12
1
4
1
3
· = Multiply.
1
2
5
12
1
12
+ =
6
12
=
The probability of getting two letters that are
either both consonants or both vowels is .
1
2
P(consonant) + P(vowel)

47. Course 3
10-5
Independent and
Dependent Events
Two mutually exclusive events cannot
both happen at the same time.
Remember!

48. The letters in the phrase I Love Math are
placed in a box.
If two letters are chosen at random, what is
the probability that they will both be
consonants?
Check It Out: Example 3A
Course 3
10-5
Independent and
Dependent Events
P(first consonant) =
5
9
Because the first letter is not replaced, the sample
space is different for the second letter, so the
events are dependant. Find the probability that the
first letter chosen is a consonant.

49. Check It Out: Example 3A Continued
Course 3
10-5
Independent and
Dependent Events
P(second consonant) =
5
18
1
2
5
9
· =
The probability of choosing two letters that are
both consonants is .
5
18
Multiply.
If the first letter chosen was a consonant, now
there would be 4 consonants and a total of 8
letters left in the box. Find the probability that
the second letter chosen is a consonant.
1
2
4
8
=

50. If two letters are chosen at random, what is
the probability that they will both be
consonants or both be vowels?
Check It Out: Example 3B
There are two possibilities: 2 consonants or 2
vowels. The probability of 2 consonants was
calculated in Try This 3A. Now find the probability
of getting 2 vowels.
Find the probability that
the first letter chosen is a
vowel.
If the first letter chosen was a vowel, there are now
only 3 vowels and 8 total letters left in the box.
Course 3
10-5
Independent and
Dependent Events
P(first vowel) =
4
9

51. Check It Out: Example 3B Continued
Find the probability that
the second letter chosen is
a vowel.
The events of both consonants and both vowels are
mutually exclusive, so you can add their probabilities.
Course 3
10-5
Independent and
Dependent Events
P(second vowel) =
3
8
12
72
3
8
4
9
· = Multiply.
1
6
=
4
9
5
18
1
6
+ =
8
18
= P(consonant) + P(vowel)
The probability of getting two letters that are
either both consonants or both vowels is .
4
9

52. Lesson Quiz
Determine if each event is dependent or
independent.
1. drawing a red ball from a bucket and then
drawing a green ball without replacing the
first
2. spinning a 7 on a spinner three times in a row
3. A bucket contains 5 yellow and 7 red balls. If 2
balls are selected randomly without
replacement, what is the probability that they
will both be yellow?
independent
dependent
Insert Lesson Title Here
5
33
Course 3
10-5
Independent and
Dependent Events