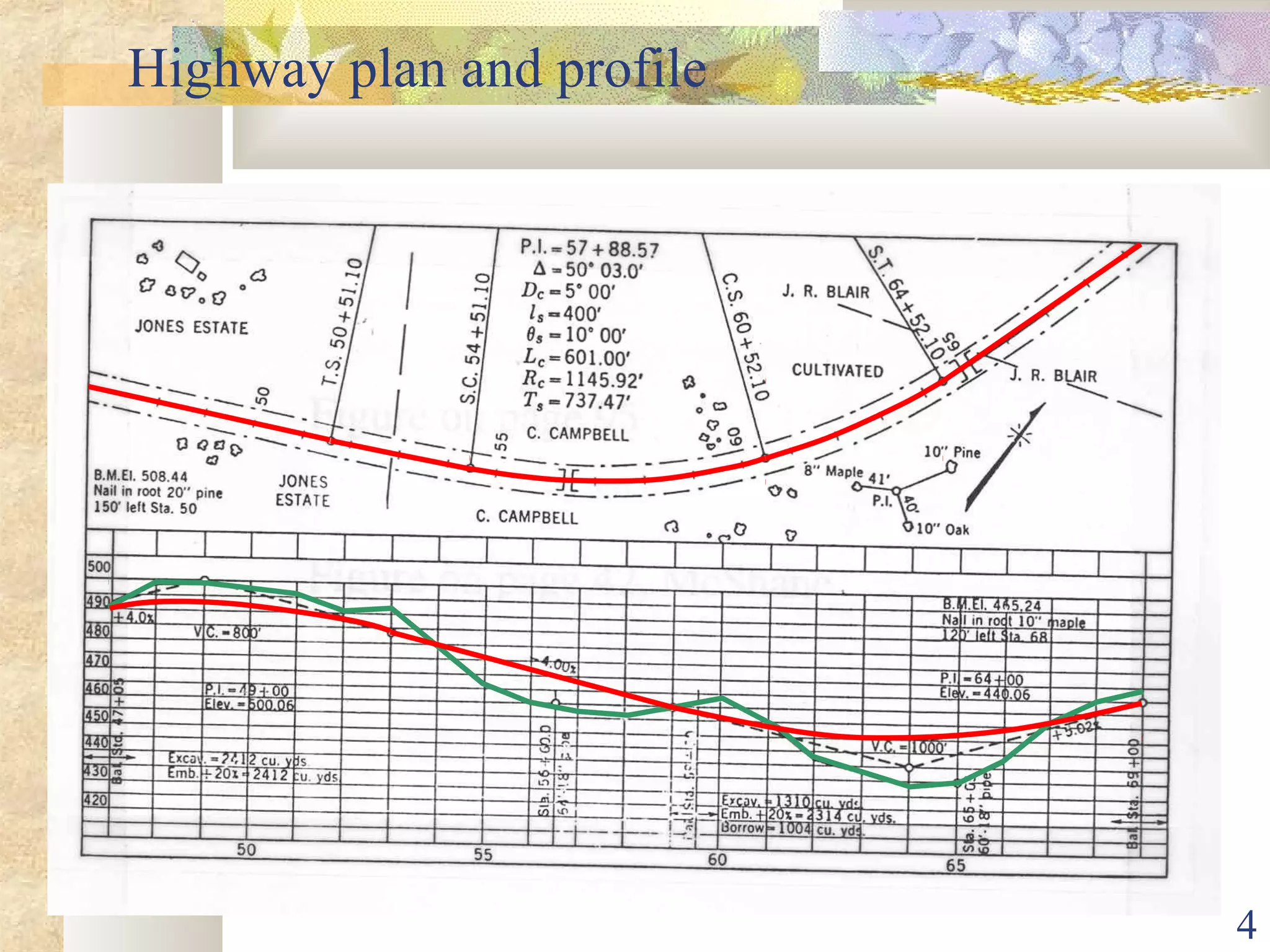
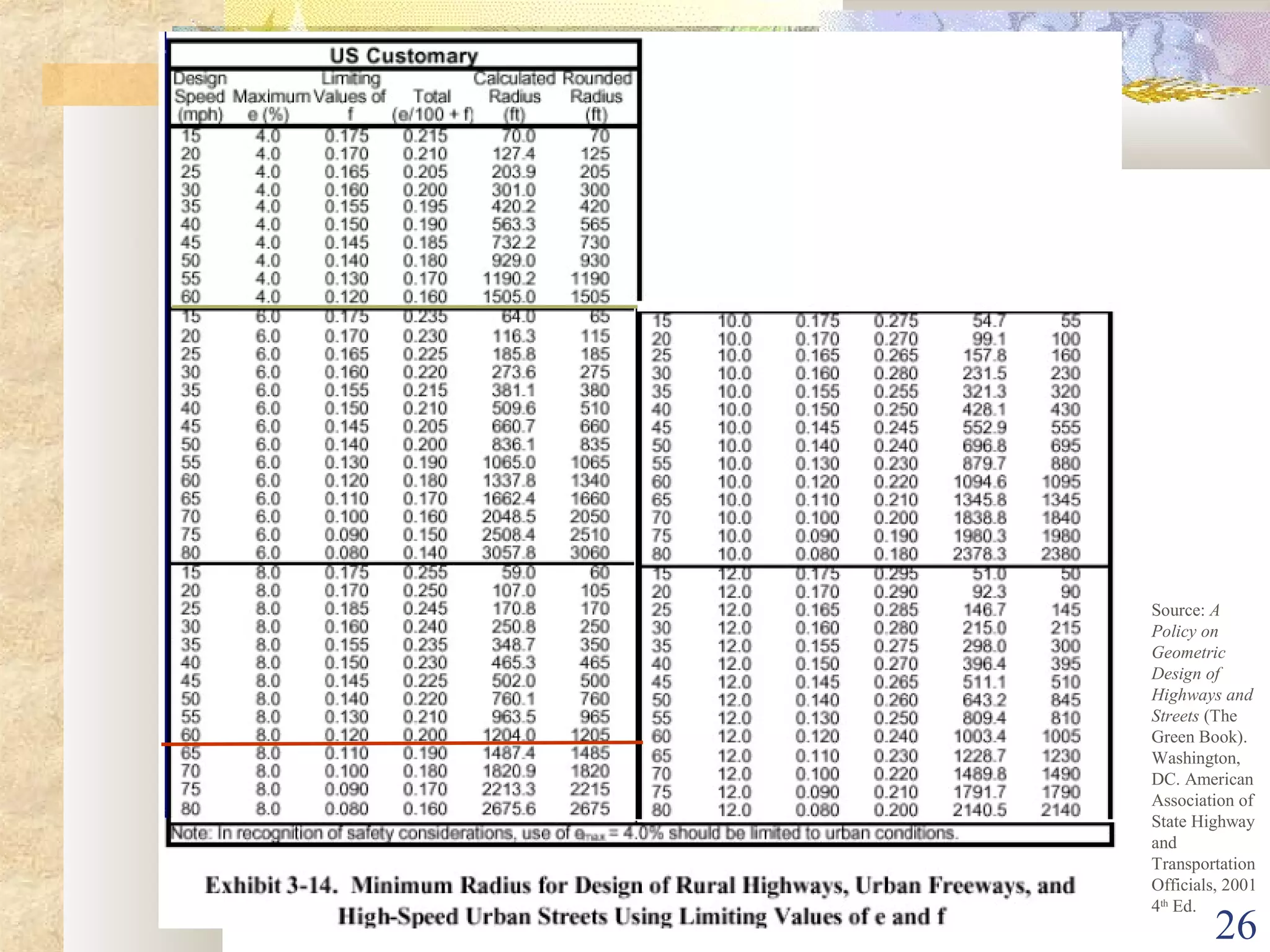
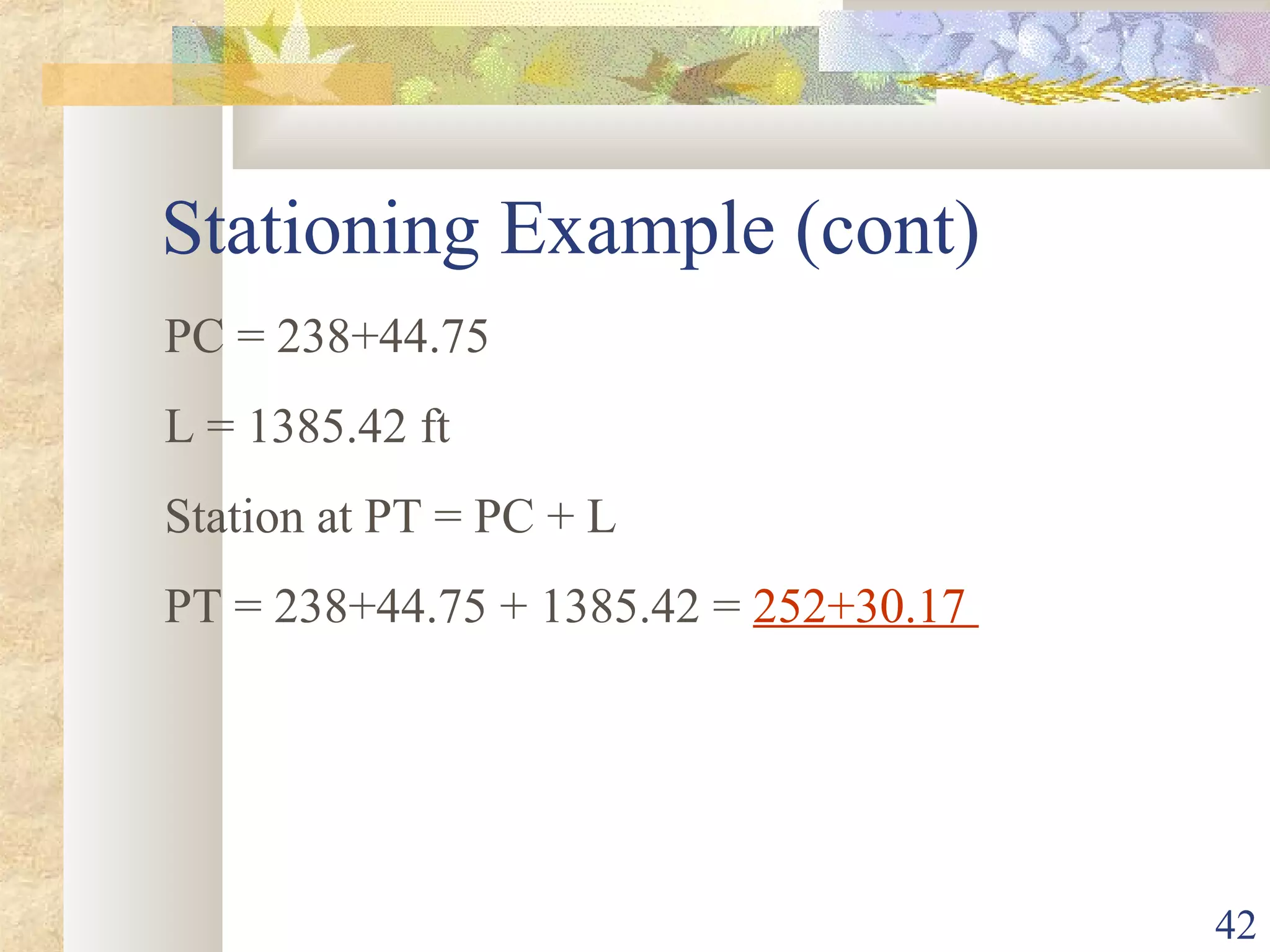
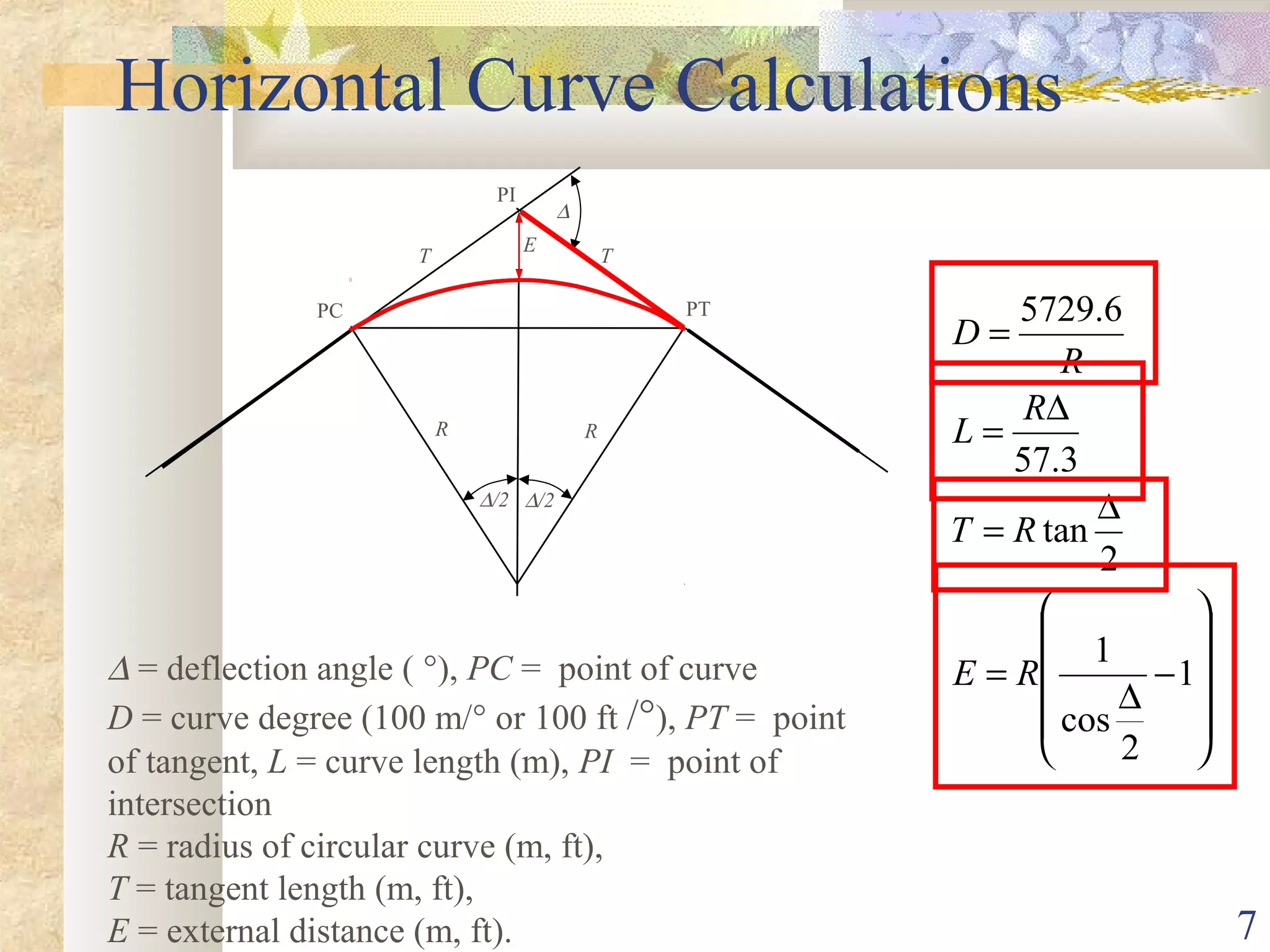
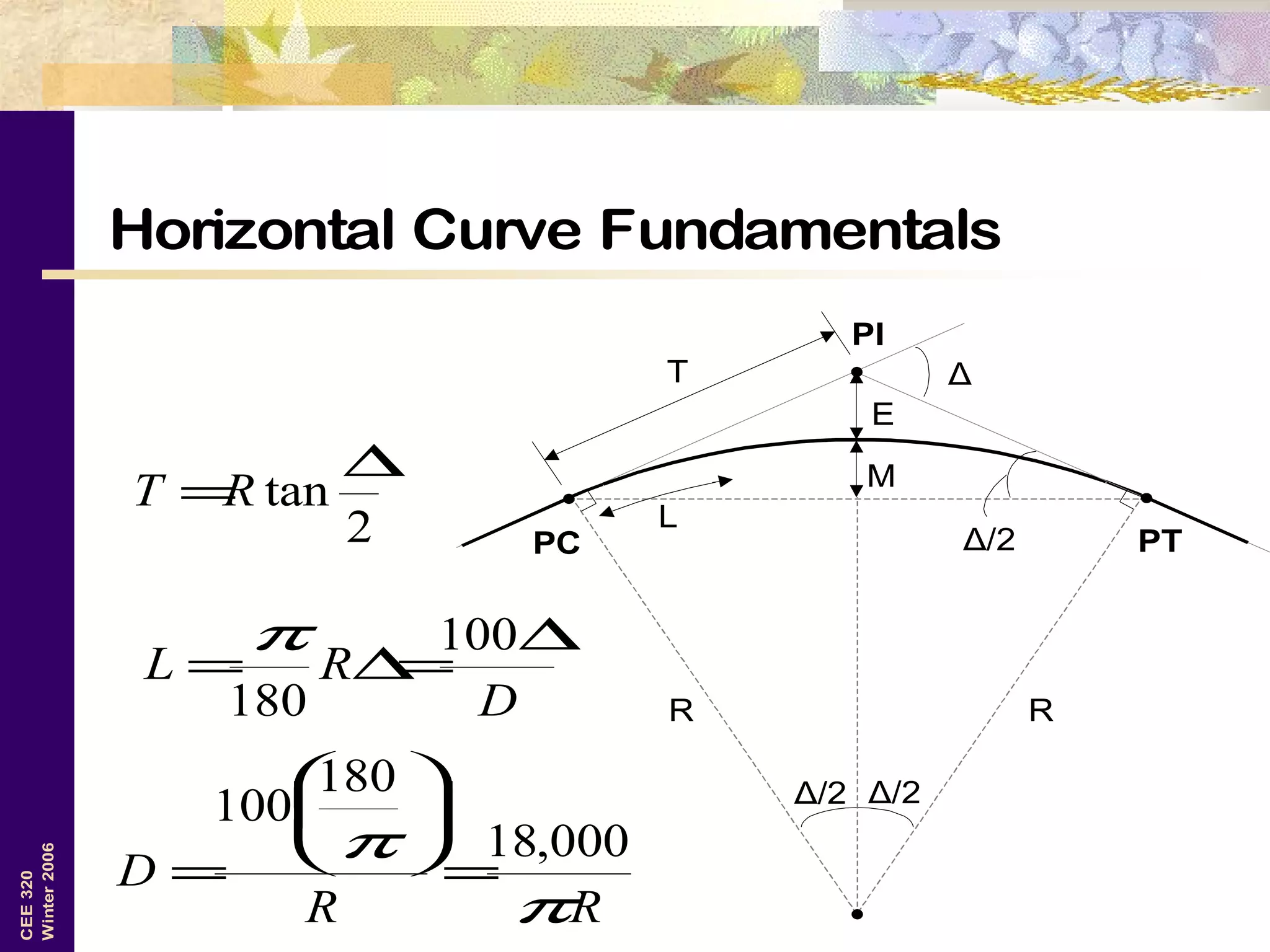
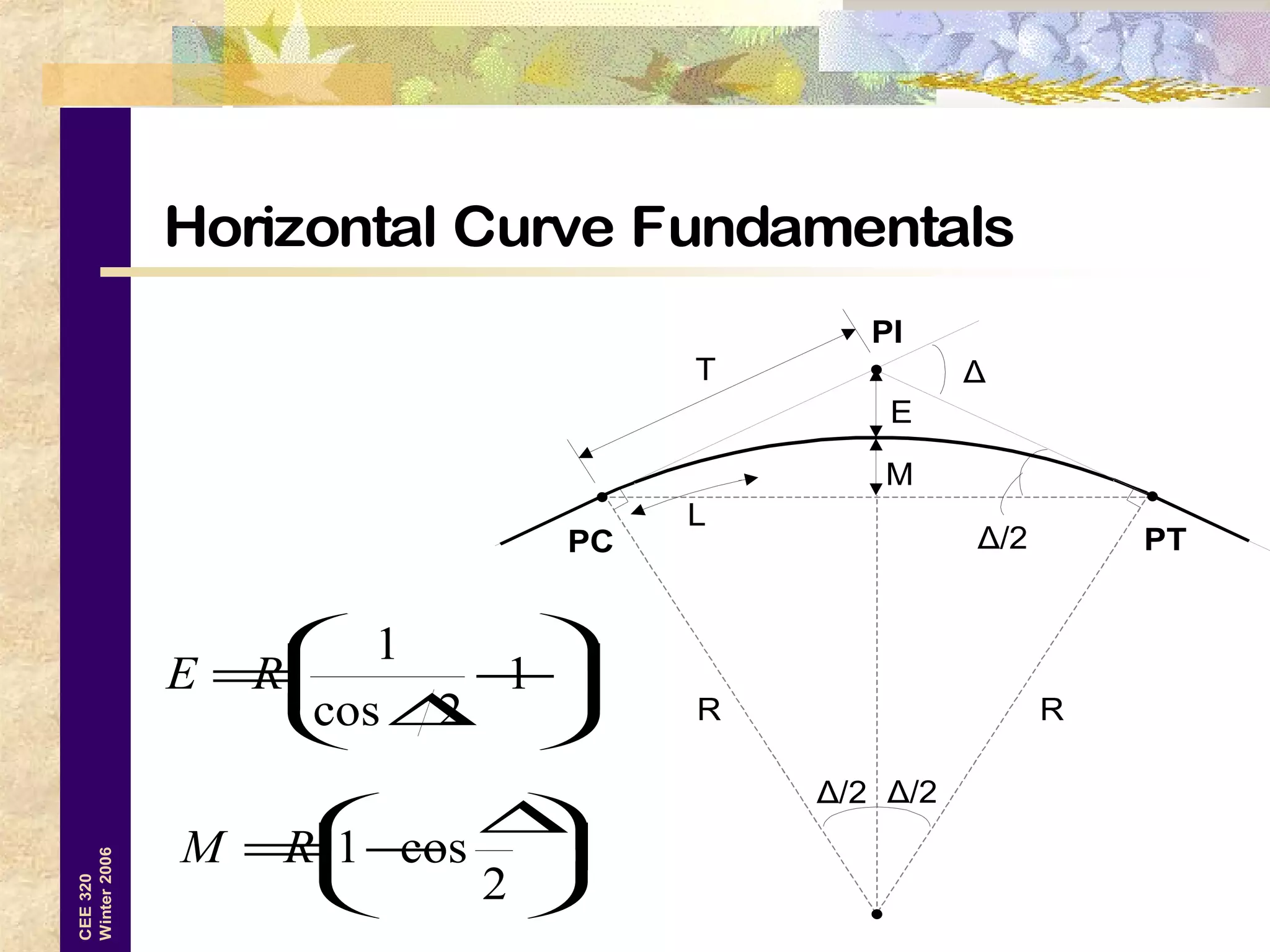
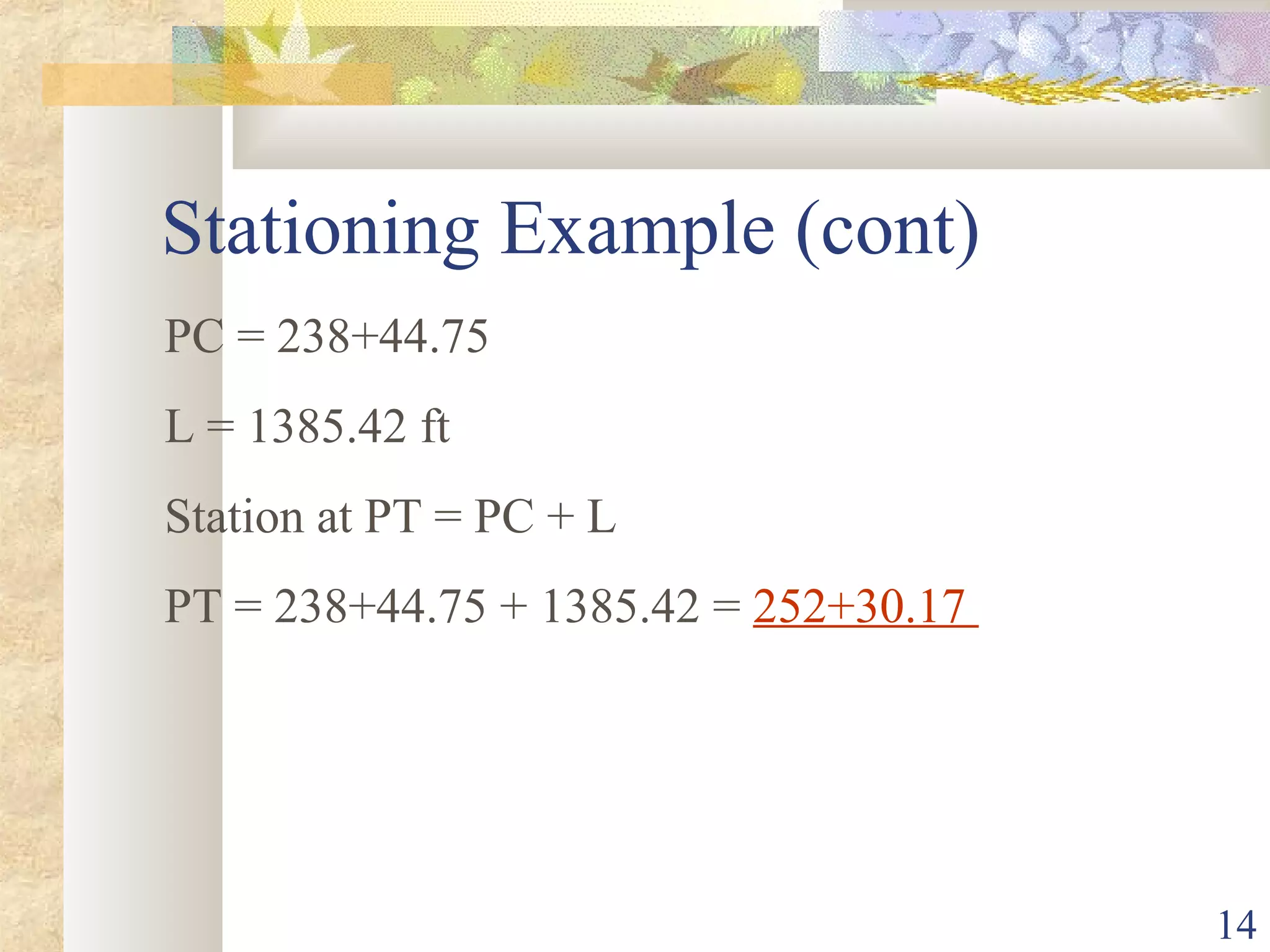
Here are the key steps and calculations for the homework: 1. Use design speed of 55 mph, emax of 4%, and fmax of 0.12 from Green Book 2. Calculate minimum radius using formula: Rmin = V2/(15(e+f)) = 1,200 ft 3. Select radius of 1,400 ft 4. Given: PI station of 352+44.97, Δ of 35° 24' 55" 5. Calculate curve length using L = ΔR/5729.58 = 1,260 ft 6. Calculate tangent length using T = Rtan(Δ/2) = 630 ft 7. Calculate PC station: PC = PI - T

1. 1
Horizontal Alignment
CE 453 Lecture 16
CEE320
Winter2006
Horizontal
Alignment

2. 2
Horizontal Alignment
1. Tangents
2. Curves
3. Transitions
Curves require superelevation (next lecture)
Reason for super: banking of curve, retard
sliding, allow more uniform speed, also
allow use of smaller radius curves (less
land)

3. 3
Curve Types
1. Simple curves with spirals (why spirals)
2. Broken Back – two curves same direction
(avoid)
3. Compound curves: multiple curves connected
directly together (use with caution) go from
large radii to smaller radii and have R(large) <
1.5 R(small)
4. Reverse curves – two curves, opposite direction
(require separation typically for superelevation
attainment)

4. 4
Highway plan and profile

5. 5
Important Components of Simple
Circular Curve
 ∆ = deflection angle ( °),
 PC = point of curve
 D = curve degree (100 m/° or 100 ft /°),
 PT = point of tangent, L = curve length (m),
 PI = point of intersection
 R = radius of circular curve (m, ft),
 T = tangent length (m, ft),
 E = external distance (m, ft).

6. 6
Important Components of Simple
Circular Curve
See: ftp://165.206.254.150/dotmain/design/dmanual/English/e02a-01.pdf
1. PC, PI, PT, E, M, and ∆
2. L = 2(π)R(∆)/360
3 T = R tan (∆/2)
Source: Iowa DOT
Design Manual
Direction of stationing

7. 7
Horizontal Curve Calculations
R R
∆
∆/2
E
T T
∆/2
PC PT
PI
∆ = deflection angle ( °), PC = point of curve
D = curve degree (100 m/° or 100 ft /°), PT = point
of tangent, L = curve length (m), PI = point of
intersection
R = radius of circular curve (m, ft),
T = tangent length (m, ft),
E = external distance (m, ft).












−
∆
=
∆
=
∆
=
=
1
2
cos
1
2
tan
3.57
6.5729
RE
RT
R
L
R
D

8. 8
CEE320
Winter2006
Horizontal Curve Fundamentals
R
T
PC PT
PI
M
E
R
Δ
Δ/2Δ/2
Δ/2
RR
D
π
π 000,18
180
100
=






=
2
tan
∆
=RT
D
RL
∆
=∆=
100
180
π
L

9. 9
CEE320
Winter2006
Horizontal Curve Fundamentals






−
∆
= 1
2cos
1
RE





 ∆
−=
2
cos1RM
R
T
PC PT
PI
M
E
R
Δ
Δ/2Δ/2
Δ/2
L

10. 10
Horizontal Curve Example
 Deflection angle of a 4º curve is 55º25’, PI at
station 245+97.04. Find length of curve,T, and
station of PT.
 D = 4º
 ∆ = 55º25’ = 55.417º
 D = _5729.58_ R = _5729.58_ = 1,432.4 ft
R 4

11. 11
Horizontal Curve Example
 D = 4º
 ∆ = 55.417º
 R = 1,432.4 ft
 L = 2πR∆ = 2π(1,432.4 ft)(55.417º) =
1385.42ft
360 360

12. 12
Horizontal Curve Example
 D = 4º
 ∆ = 55.417º
 R = 1,432.4 ft
 L = 1385.42 ft
 T = R tan ∆ = 1,432.4 ft tan (55.417) = 752.29 ft
2 2

13. 13
Stationing Example
Stationing goes around horizontal curve.
For previous example, what is station of PT?
First calculate the station of the PC:
PI = 245+97.04
PC = PI – T
PC = 245+97.04 – 752.29 = 238+44.75

14. 14
Stationing Example (cont)
PC = 238+44.75
L = 1385.42 ft
Station at PT = PC + L
PT = 238+44.75 + 1385.42 = 252+30.17

15. 15
CEE320
Winter2006
Example 4
A horizontal curve is designed with a 1500 ft. radius. The tangent
length is 400 ft. and the PT station is 20+00. What are the PI and PC
stations?

16. 16
CEE320
Winter2006
Solution
• Since we know R and T we can use
• T = R tan(delta/2) to get delta = 29.86 degrees
• D = 5729.6/R. Therefore D = 3.82
• L = 100(delta)/D = 100(29.86)/3.82 = 781 ft.
• PC = PT – L = 2000 – 781 = 12+18.2
• PI = PC +T = 12+18.2 + 400 = 16+18.2.
• Note: cannot find PI by subtracting T from PT!

17. 17
Design of Horizontal Alignment
Determination of
 Minimum Radius
 Length of curve
 Computation of offsets from the tangents to
the curve to facilitate the setting out of
t6hye curve

18. 18
Horizontal Curve design
 Design based on appropriate relationship
between design speed and curvature and
their relationship with side friction and
superelevation
 Turning the front wheels, side friction and
superelevation generate an acceleration
toward center of curvature (centripetal
acceleration)

19. 19
Motion on Circular Curves
dt
dv
at =
R
v
an
2
=

20. 20
βββ coscossin ns amWfW =+
ββββ cos
cos)(cossin
2
WR
v
g
W
WfW s =+
e== β
β
β
tan
cos
sin
gR
v
fe s
2
=+
Motion on
Circular
Curves

21. 21
Vehicle Stability on Curves
where:
gR
v
fe s
2
=+
(ft/s),speeddesign=v
(-),tcoefficienfrictionside=sf
).ft/s(32onacceleratigravity 2
=g
(-),tionsupereleva=e
(ft),radius=R
Assumed
Design
speed
(mph)
Maximum
design
fs max
20 0.17
70 0.10
Must not be too short
(0.12)0.10-0.06max =e

22. 22
Radius Calculation
Rmin
= ___V2
______
15(e + f)
Where:
Rmin is the minimum radius in feet
V = velocity (mph)
e = superelevation
f = friction (15 = gravity and unit conversion)

23. 23
Radius Calculation
• Rmin
uses max e and max f (defined by AASHTO, DOT,
and graphed in Green Book) and design speed
• f is a function of speed, roadway surface, weather
condition, tire condition, and based on comfort – drivers
brake, make sudden lane changes, and change position
within a lane when acceleration around a curve becomes
“uncomfortable”
• AASHTO: 0.5 @ 20 mph with new tires and wet
pavement to 0.35 @ 60 mph
• f decreases as speed increases (less tire/pavement
contact)

24. 24
Max e
 Controlled by 4 factors:
 Climate conditions (amount of ice and snow)
 Terrain (flat, rolling, mountainous)
 Type of area (rural or urban)
 Frequency of slow moving vehicles who
might be influenced by high superelevation
rates

25. 25
Max e
 Highest in common use = 10%, 12% with no
ice and snow on low volume gravel-surfaced
roads
 8% is logical maximum to minimize slipping
by stopped vehicles, considering snow and
ice
 Iowa uses a maximum of 6% on new projects
 For consistency use a single rate within a
project or on a highway

26. 26
Source: A
Policy on
Geometric
Design of
Highways and
Streets (The
Green Book).
Washington,
DC. American
Association of
State Highway
and
Transportation
Officials, 2001
4th
Ed.

27. 27
Radius Calculation (Example)
Design radius example: assume a maximum e
of 8% and design speed of 60 mph, what is
the minimum radius?
fmax = 0.12 (from Green Book)
Rmin
= _____602
________________
15(0.08 + 0.12)
Rmin = 1200 feet

28. 28
Radius Calculation (Example)
For emax = 4%? (urban situation)
Rmin
= _____602
________________
15(0.04 + 0.12)
Rmin = 1,500 feet

29. 29
Radius Calculation (Example)
For emax = 2%? (rotated crown)
Rmin
= _____602
________________
15(0.02 + 0.12)
Rmin = 1,714 feet

30. 30
Radius Calculation (Example)
For emax = -2%? (normal crown, adverse
direction)
Rmin
= _____602
________________
15(-0.02 + 0.12)
Rmin = 2,400 feet

31. Sight Distance for Horizontal
Curves
31

32. 32
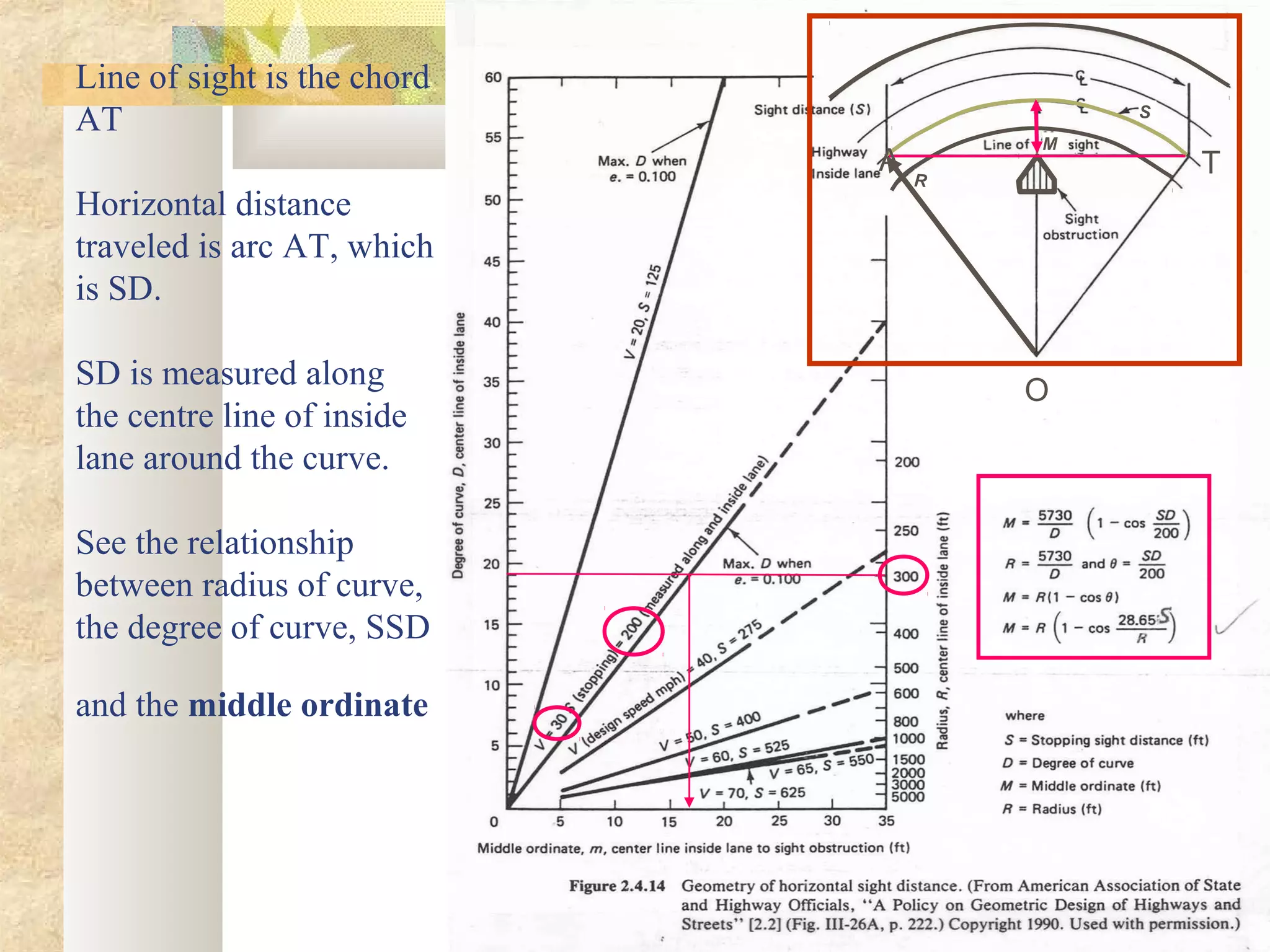
Sight Distance for Horizontal Curves
 Location of object along chord length that blocks
line of sight around the curve
 m = R(1 – cos [28.65 S])
R
Where:
m = line of sight
S = stopping sight distance
R = radius

33. 33
Sight Obstruction on Horizontal
Curves
 Assume S is the SSD equal to chord AT
 Angle subtended at centre of circle by arc AT
is 2θ in degree then
 Total circumference perimeter (πR)
 S / πR = 2θ / 180
 S = 2R θπ / 180
 θ = S 180/ 2R π = 28.65 (S) / R
 R-M/R = cos θ
 M = R [1 – cos 28.65 (S) / R ]
θR
M
A T
B
T
O
O
θ
B

34. 34
Line of sight is the chord
AT
Horizontal distance
traveled is arc AT, which
is SD.
SD is measured along
the centre line of inside
lane around the curve.
See the relationship
between radius of curve,
the degree of curve, SSD
and the middle ordinate
S
R
M
O
TA

35. 35
Sight Distance Example
A horizontal curve with R = 800 ft is part of a 2-lane
highway with a posted speed limit of 35 mph.
What is the minimum distance that a large
billboard can be placed from the centerline of the
inside lane of the curve without reducing required
SSD? Assume p/r =2.5 and a = 11.2 ft/sec2
SSD = 1.47vt + _________v2
____
30(__a___ ± G)
32.2

36. 36
Sight Distance Example
SSD = 1.47(35 mph)(2.5 sec) +
_____(35 mph)2
____ = 246 feet
30(__11.2___ ± 0)
32.2

37. 37
Sight Distance Example
m = R(1 – cos [28.65 S])
R
m = 800 (1 – cos [28.65 {246}]) = 9.43 feet
800
(in radians not degrees)

38. 38
Horizontal Curve Example
 Deflection angle of a 4º curve is 55º25’, PI at
station 245+97.04. Find length of curve,T, and
station of PT.
 D = 4º
 ∆ = 55º25’ = 55.417º
 D = _5729.58_ R = _5729.58_ = 1,432.4 ft
R 4

39. 39
Horizontal Curve Example
 D = 4º
 ∆ = 55.417º
 R = 1,432.4 ft
 L = 2πR∆ = 2π(1,432.4 ft)(55.417º) =
1385.42ft
360 360

40. 40
Horizontal Curve Example
 D = 4º
 ∆ = 55.417º
 R = 1,432.4 ft
 L = 1385.42 ft
 T = R tan ∆ = 1,432.4 ft tan (55.417) = 752.29 ft
2 2

41. 41
Stationing Example
Stationing goes around horizontal curve.
For previous example, what is station of PT?
First calculate the station of the PC:
PI = 245+97.04
PC = PI – T
PC = 245+97.04 – 752.29 = 238+44.75

42. 42
Stationing Example (cont)
PC = 238+44.75
L = 1385.42 ft
Station at PT = PC + L
PT = 238+44.75 + 1385.42 = 252+30.17

43. 43
Suggested Steps in Horizontal
Design
1. Select tangents, PIs, and general curves making
sure you meet minimum radius criteria
2. Select specific curve radii/spiral and calculate
important points (see lab) using formula or table
(those needed for design, plans, and lab
requirements)
3. Station alignment (as curves are encountered)
4. Determine super and runoff for curves and put in
table (see next lecture for def.)
5. Add information to plans

44. 44
HOMEWORK
 Your team is responsible for the design of
a small roadway project in Iowa. Your
individual task is to design a horizontal
curve to the right using an even value
radius slightly larger than the minimum
radius curve. Use a design speed of 55
mph and a superelevation rate of 4%.
Assume the PI has a station of 352+44.97;
the Δ (delta) of the curve is 35° 24’ 55”.

45. 45
HOMEWORK
 Referring to the Iowa DOT Design
Manual you find guidance at
ftp://165.206.203.34/design/dmanual/02a-01.pd
on the design of horizontal curves.

46. 46
HOMEWORK
Your assignment:
 Reading carefully the design guidance
with special attention to the items to be
included on the plans, calculate all of the
values to be shown on a plan set for this
curve. Be sure to calculate the stations of
the PC and PT in addition to the values
listed.

47. 47
HOMEWORK
Your assignment:
 At this time do not concern yourself with
superelevation runoff; just use the design
speed and superelevation rate to determine
the minimum radius curve allowable. It
may help you to create a list of the items
to be included before doing your
calculations.

48. 48
HOMEWORK
Your assignment:
 Now use a design speed of 60 mph and
the same 4% superelevation rate to
calculate the curve. Your PI station and Δ
will remain unchanged.