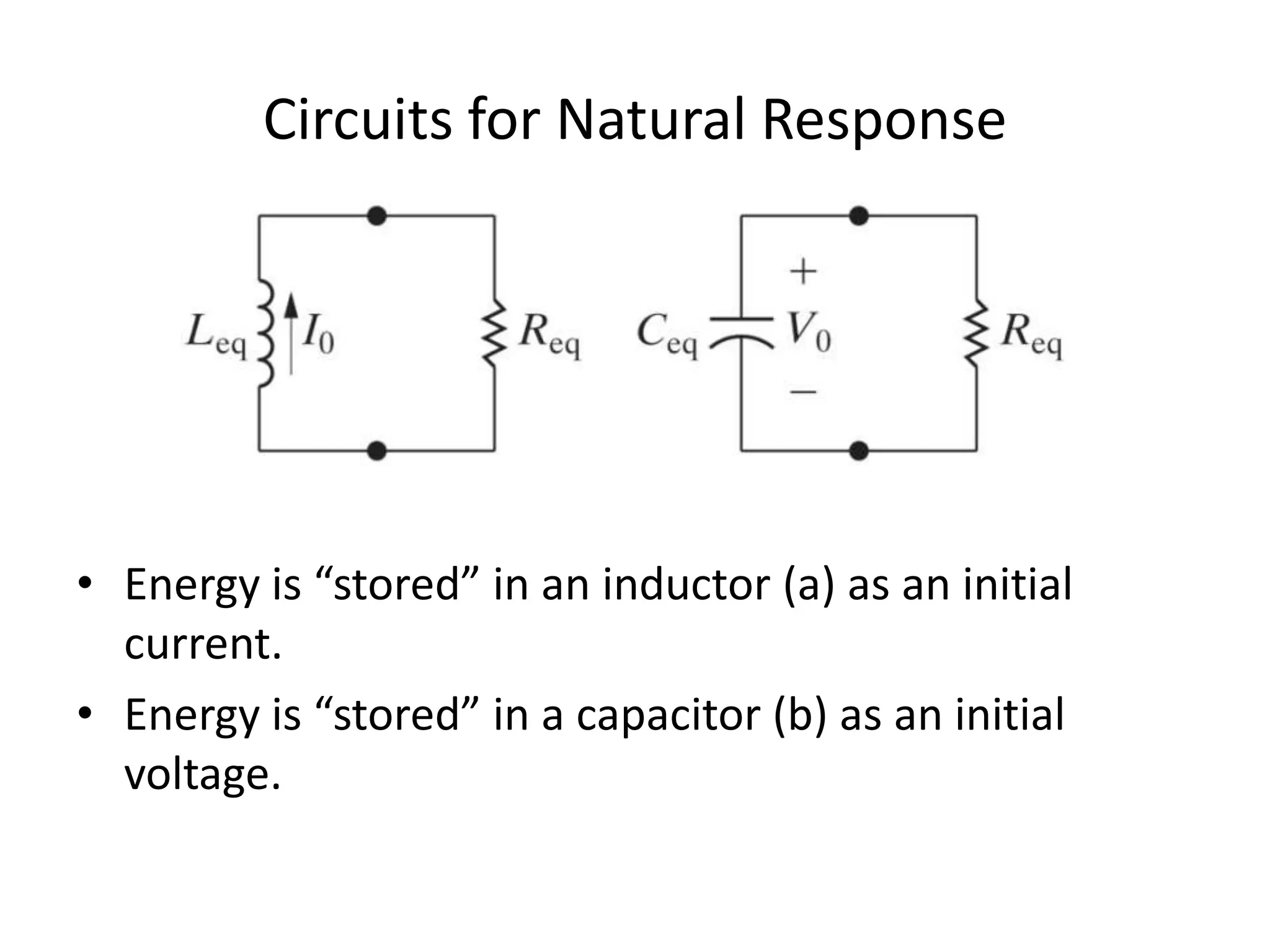
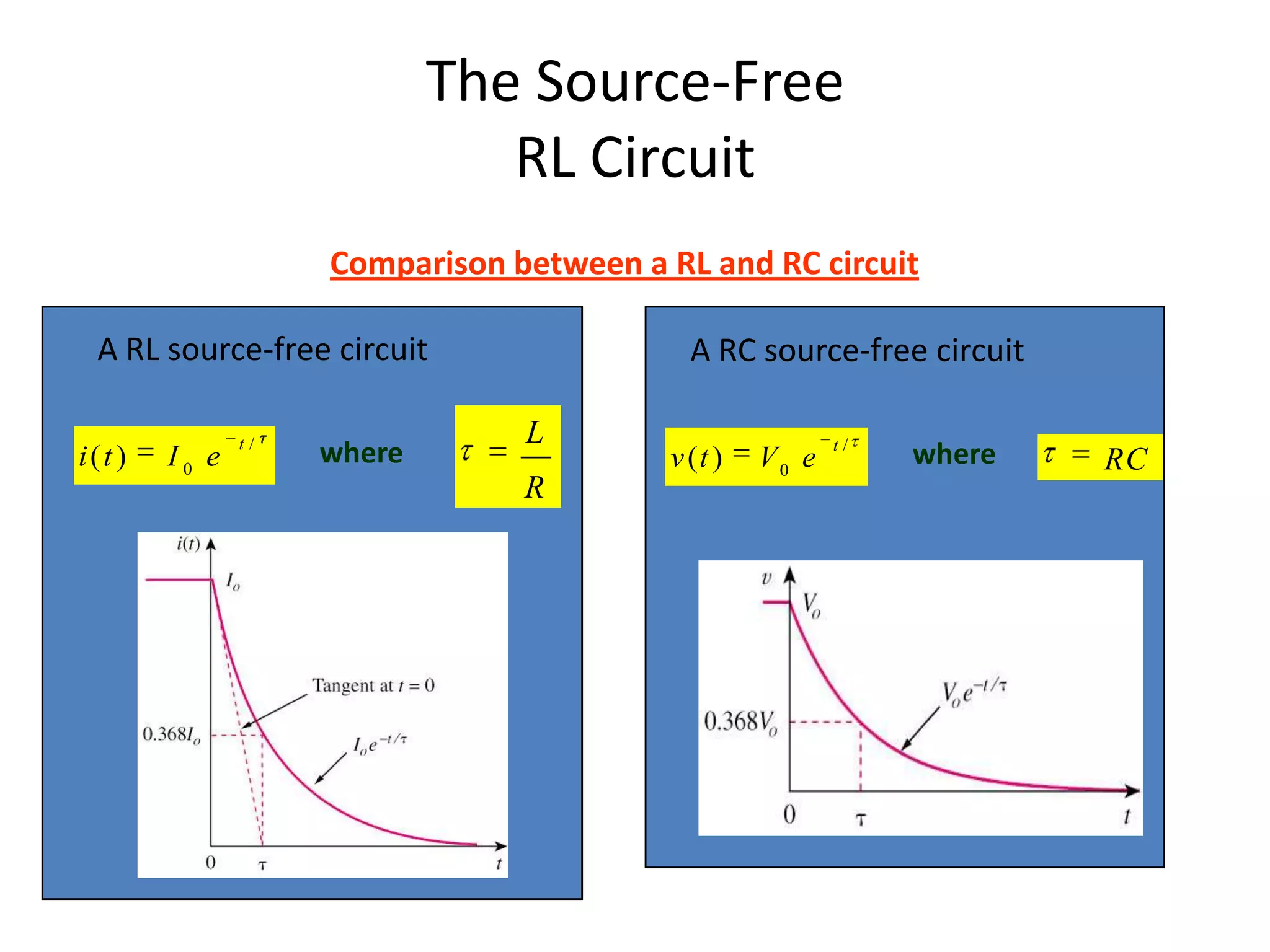
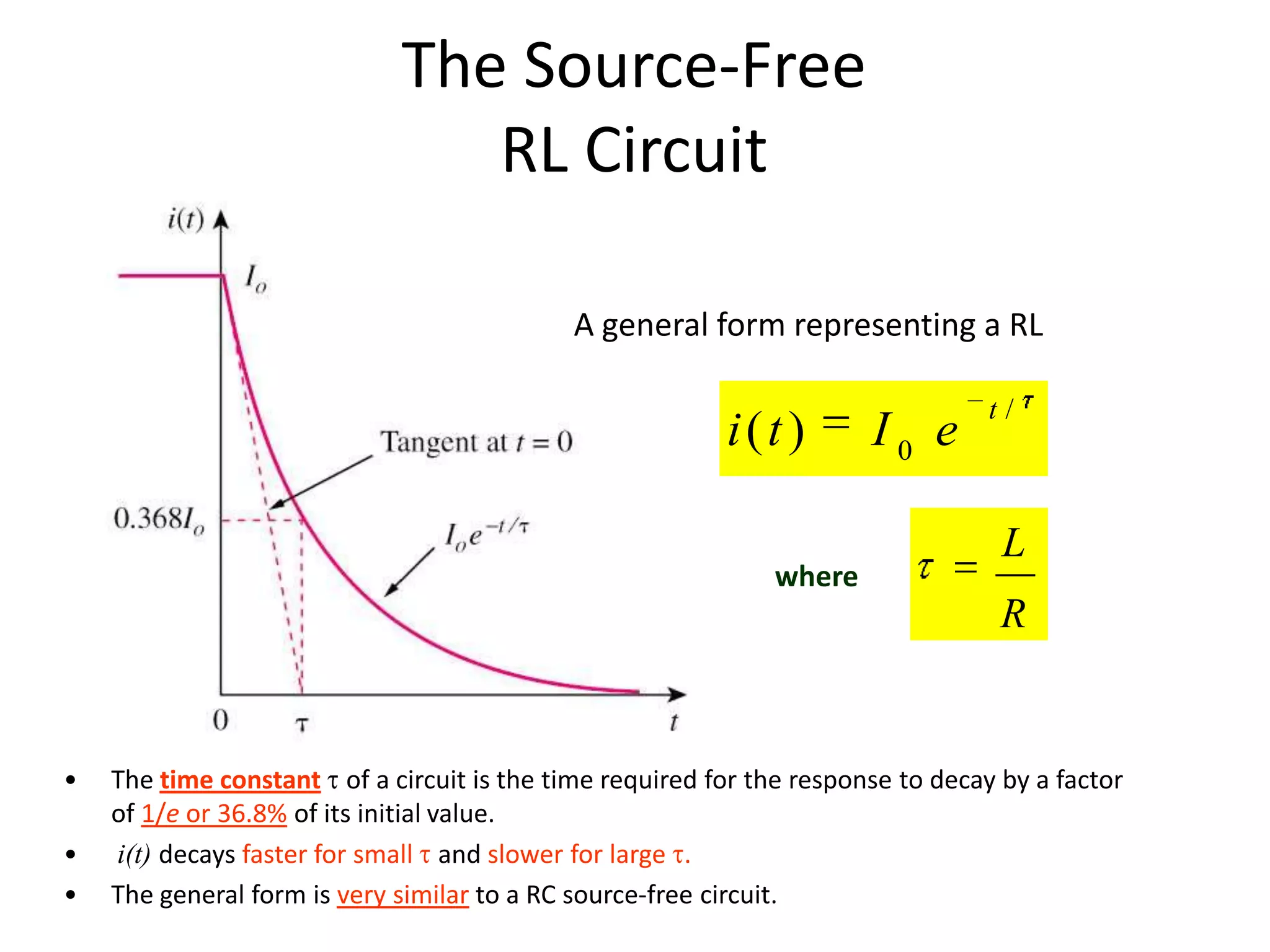
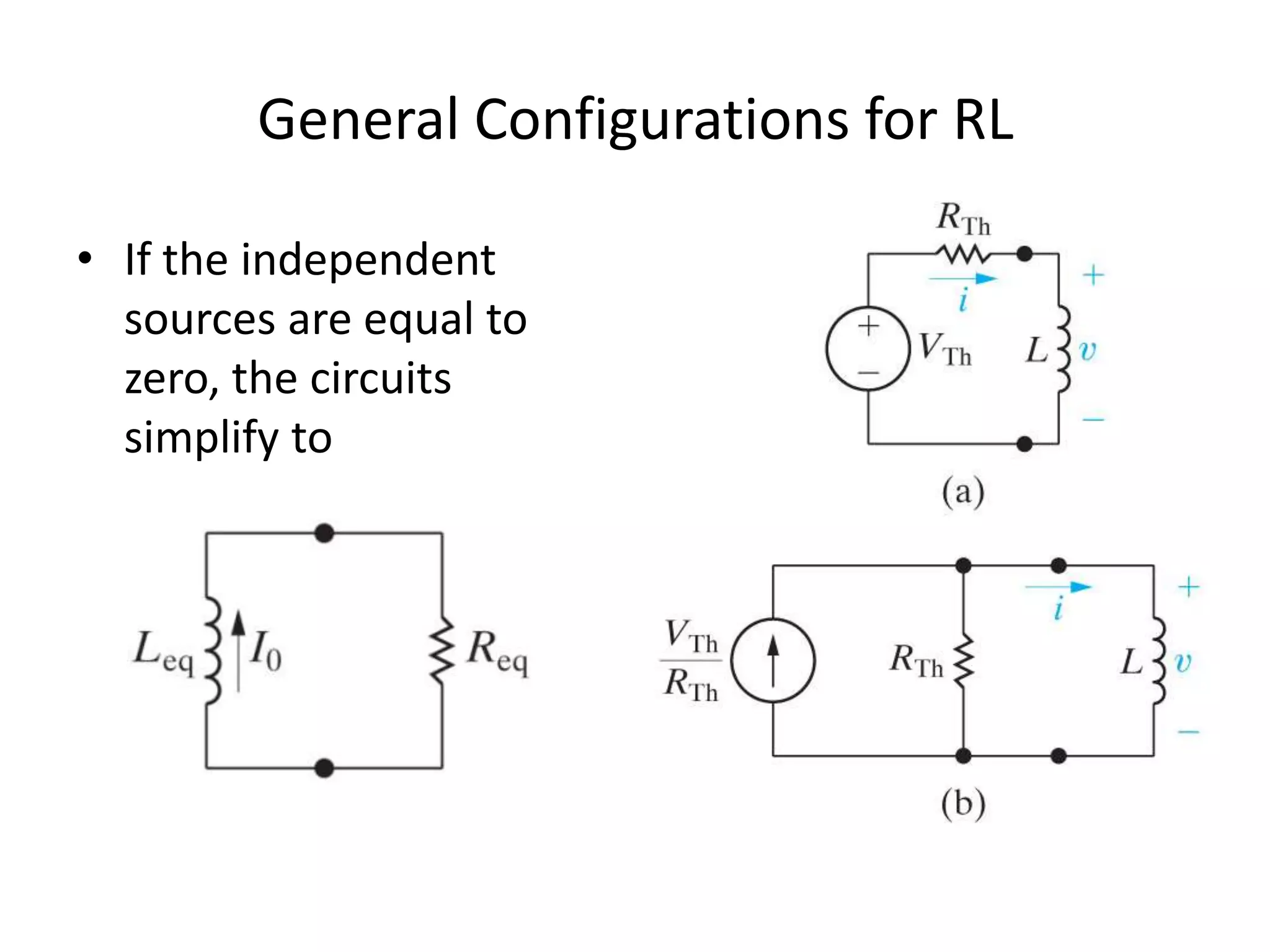
- The natural response of a circuit refers to the behavior of the circuit when external sources are removed. This allows the stored energy in inductors and capacitors to dissipate. - The general solution for the natural response of RL and RC circuits is an exponential decay from an initial value to a final value, with the decay rate determined by the circuit time constant. - For an RL circuit, the inductor current decays exponentially with time constant L/R. For an RC circuit, the capacitor voltage decays exponentially with time constant RC.

1. Natural and step response
Ahsan Khawaja

2. Cont. inductor
V
L
di
dt
• Where
V= voltage between inductor in (volt)
L= inductor in (henery)
= rate of change of current flow in amper
di
= rate of change of time in second
dt

3. dv
Cont. capacitor
• Mathematical relation
.
i
C
dv
dt
• Where
i= current that in capacitor in (ampere)
C= capacitance in (farad)
d v = rated of change of voltage.
d t = rate of change of time in second

4. First-Ordersources, resistors and an
Circuits
A circuit that contains only
•
inductor is called an RL circuit.
• A circuit that contains only sources, resistors and a
capacitor is called an RC circuit.
• RL and RC circuits are called first-order circuits
because their voltages and currents are described by
first-order differential equations.
R
i
i
L
vs
–
+
–
+
vs
R
C

5. 6 Different First-Order Circuits
There are six different STC circuits. These
are listed below.
• An inductor and a resistance (called RL
Natural Response).
• A capacitor and a resistance (called RC
Natural Response).
• An inductor and a Thévenin equivalent
(called RL Step Response).
• An inductor and a Norton equivalent
(also called RL Step Response).
• A capacitor and a Thévenin equivalent
(called RC Step Response).
• A capacitor and a Norton equivalent
(also called RC Step Response).
RX
LX
CX
RX
RX
+
vS
LX
-
iS
RX
iS
RX
LX
RX
+
vS
CX
-
These are the simple, first-order cases.
Many circuits can be reduced to one of
these six cases. They all have solutions
which are in similar forms.
CX

6. 6 Different First-Order Circuits
These are the simplest cases, so we
handle them first.
There are six different STC circuits. These
are listed below.
• An inductor and a resistance (called RL
Natural Response).
RX
CX
RX
LX
• A capacitor and a resistance (called RC
Natural Response).
RX
• An inductor and a Thévenin equivalent
+
vS
iS
RX
LX
LX
(called RL Step Response).
• An inductor and a Norton equivalent
(also called RL Step Response).
• A capacitor and a Thévenin equivalent
RX
+
vS
iS
RX
CX
(called RC Step Response).
• A capacitor and a Norton equivalent
(also called RC Step Response).
These are the simple, first-order cases.
CX
They all have solutions which are in similar
forms.

7. The Natural Response of a Circuit
• The currents and voltages that arise when
energy stored in an inductor or capacitor is
suddenly released into a resistive circuit.
• These “signals” are determined by the circuit
itself, not by external sources!

8. Step Response
• The sudden application of a DC voltage or
current source is referred to as a “step”.
• The step response consists of the voltages and
currents that arise when energy is being
absorbed by an inductor or capacitor.

9. Circuits for Natural Response
• Energy is “stored” in an inductor (a) as an initial
current.
• Energy is “stored” in a capacitor (b) as an initial
voltage.

10. General Configurations for RL
• If the independent
sources are equal to
zero, the circuits
simplify to

11. Natural Response of an RL Circuit
• Consider the circuit shown.
• Assume that the switch has been closed “for a
long time”, and is “opened” at t=0.

12. What does “for a long time” Mean?
• All of the currents and voltages have reached
a constant (dc) value.
• What is the voltage across the inductor just
before the switch is opened?

13. Just before t = 0
• The voltage across the inductor is equal to
zero.
• There is no current in either resistor.
• The current in the inductor is equal to IS.

14. Just after t = 0
• The current source and its parallel resistor R0
are disconnected from the rest of the circuit,
and the inductor begins to release energy.

15. The Source-Free
RL Circuit
• A first-order RL circuit consists of a inductor L (or its
equivalent) and a resistor (or its equivalent)
By KVL
vL
L
vR
di
0
iR
0
dt
Inductors law
Ohms law
di
R
i
L
dt
i (t )
I0 e
Rt/L

16. The Source-Free
RC Circuit
• A first-order circuit is characterized by a first-order
differential equation.
By KCL
iR
iC
Ohms law
•
•
0
v
C
R
dv
dt
Capacitor law
Apply Kirchhoff’s laws to purely resistive circuit results in algebraic equations.
Apply the laws to RC and RL circuits produces differential equations.
0

17. Natural Response of an RL Circuit
• Consider the following circuit, for which the switch is closed
for t < 0, and then opened at t = 0:
t=0
Io
Ro
i
L
+
R
v
–
Notation:
0– is used to denote the time just prior to switching
0+ is used to denote the time immediately after switching
• The current flowing in the inductor at t = 0– is Io

18. Solving for the Current (t
0)
• For t > 0, the circuit reduces to
i
Io
Ro
L
+
R
v
–
• Applying KVL to the LR circuit:
• Solution:
i (t )
i(0)e
( R / L ) t = I e-(R/L)t
0

19. Solving for the Voltage (t > 0)
i (t )
( R / L )t
Ioe
+
Io
Ro
L
R
v
–
• Note that the voltage changes abruptly:
v( 0 )
0
for t 0, v(t)
v( 0 )
iR
I0R
I o Re
( R /L )t

20. Time Constant
• In the example, we found that
i (t )
I oe
( R / L )t
and
v (t )
I o Re
L
• Define the time constant
( R / L )t
(sec)
R
– At t = , the current has reduced to 1/e (~0.37) of its
initial value.
– At t = 5 , the current has reduced to less than 1% of
its initial value.

21. The Source-Free
RL Circuit
Comparison between a RL and RC circuit
A RL source-free circuit
i(t )
I0 e
t/
where
A RC source-free circuit
L
R
v (t )
V0 e
t/
where
RC

22. The Complete Solution
R
i (t )
Ie
0
L
t
,t
0

23. The voltage drop across the resistor
v
iR
R
v
I Re
L
0
t
,t
v(0 )
0
v(0 )
I R
0
0
.

24. The Power Dissipated in the Resistor
p
vi
v
2
iR
2
R
p
2
I Re
0
2
R
L
t
,t
0

25. The Energy Delivered to the Resistor
t
w
t
pdx
w
2
0
0
2
2
I R (1
e
0
L
t
,w
R
L
I Re
0
1
R
2
2
1
2
LI
2
0
x
dx
R
L
t
),t
0.

26. The Source-Free
RL Circuit
A general form representing a RL
i(t )
where
I0 e
t/
L
R
•
•
•
The time constant of a circuit is the time required for the response to decay by a factor
of 1/e or 36.8% of its initial value.
i(t) decays faster for small and slower for large .
The general form is very similar to a RC source-free circuit.

27. The Source-Free
RC Circuit
• The natural response of a circuit refers to the behavior (in terms of
voltages and currents) of the circuit itself, with no external sources of
excitation.
Time constant
RC
Decays more slowly
Decays faster
•
•
The time constant of a circuit is the time required for the response to decay by a
factor of 1/e or 36.8% of its initial value.
v decays faster for small and slower for large .

28. Natural Response Summary
RL Circuit
RC Circuit
i
+
L
C
R
v R
–
• Inductor current cannot
change instantaneously
i(0 )
i (t )
•
i(0 )
i(0)e
• time constant
Capacitor voltage cannot
change instantaneously
v (0 )
t/
v (t )
L
R
•
v (0 )
v (0)e
time constant
t/
RC

29. General Solution for Natural and Step Responses
of RL and RC Circuits
( t t0 )
x (t )
xf
[ x (t 0 )
x f ]e
Final Value
Time Constant
Initial Value
Determine the initial and final values of the
variable of interest and the time constant of the
circuit.
Substitute into the given expression.

30. Example
b
R1
400kOhm
V1
90 V
a
R3
20 Ohm
J1
Key = Space
+
vC(t)
R2
60 Ohm
V2
40 V
C
0.5uF
-
• What is the initial value of vC?
• What is the final value of vC?
• What is the time constant when the switch is in
position b?
• What is the expression for vC(t) when t>=0?

31. Initial Value of vC
b
R1
400kOhm
a
R3
20 Ohm
J1
+
V1
90 V
Key = Space
V60
+
vC(0)
C
0.5uF
R2
60 Ohm
V2
40 V
-
-
• The capacitor looks like an open circuit, so the
voltage @ C is the same as the voltage @ 60Ω.
v C (0 )
60
4 0V
20
3 0V
60

32. Final Value of vC
b
R1
400kOhm
V1
90 V
a
R3
20 Ohm
J1
Key = Space
+
vC(∞)
R2
60 Ohm
V2
40 V
C
0.5uF
-
• After the switch is in position b for a long time, the
capacitor will look like an open circuit again, and the
voltage @ C is +90 Volts.

33. The time constant of the circuit when the switch
is in position b
R1
400kOhm
V1
90 V
b
a
R3
20 Ohm
J1
Key = Space
R2
60 Ohm
C
0.5uF
• The time constant τ = RC = (400kΩ)(0.5μF)
• τ = 0.2 s
V2
40 V

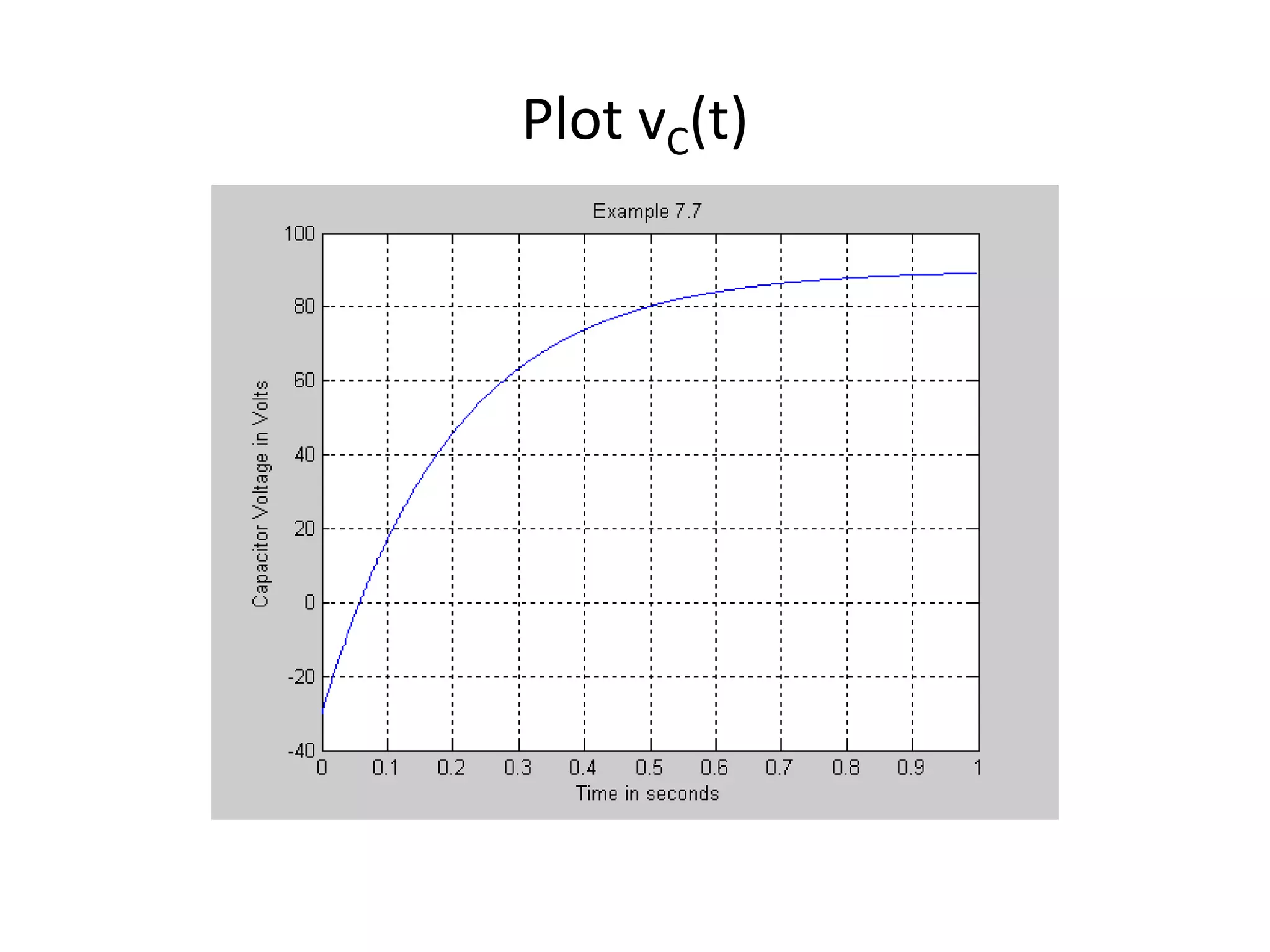
34. The expression for vC(t) for t>=0
t
vC (t )
vC ( )
[ v C (0)
v C ( )]e
t
vC (t )
90
[ 30
vC (t )
90
120 e
90]e
5t
V
0.2

35. The expression for i(t) for t>=0
b
R1
a
400kOhm
R3
20 Ohm
J1
Key = Space
V1
90 V
i(t)
30V
R2
60 Ohm
V2
40 V
C
0.5uF
+
• Initial value of i is (90 - - 30)V/400kΩ = 300μA
• Final value of i is 0 – the capacitor charges to +90 V
and acts as an open circuit
• The time constant is still τ = 0.2 s

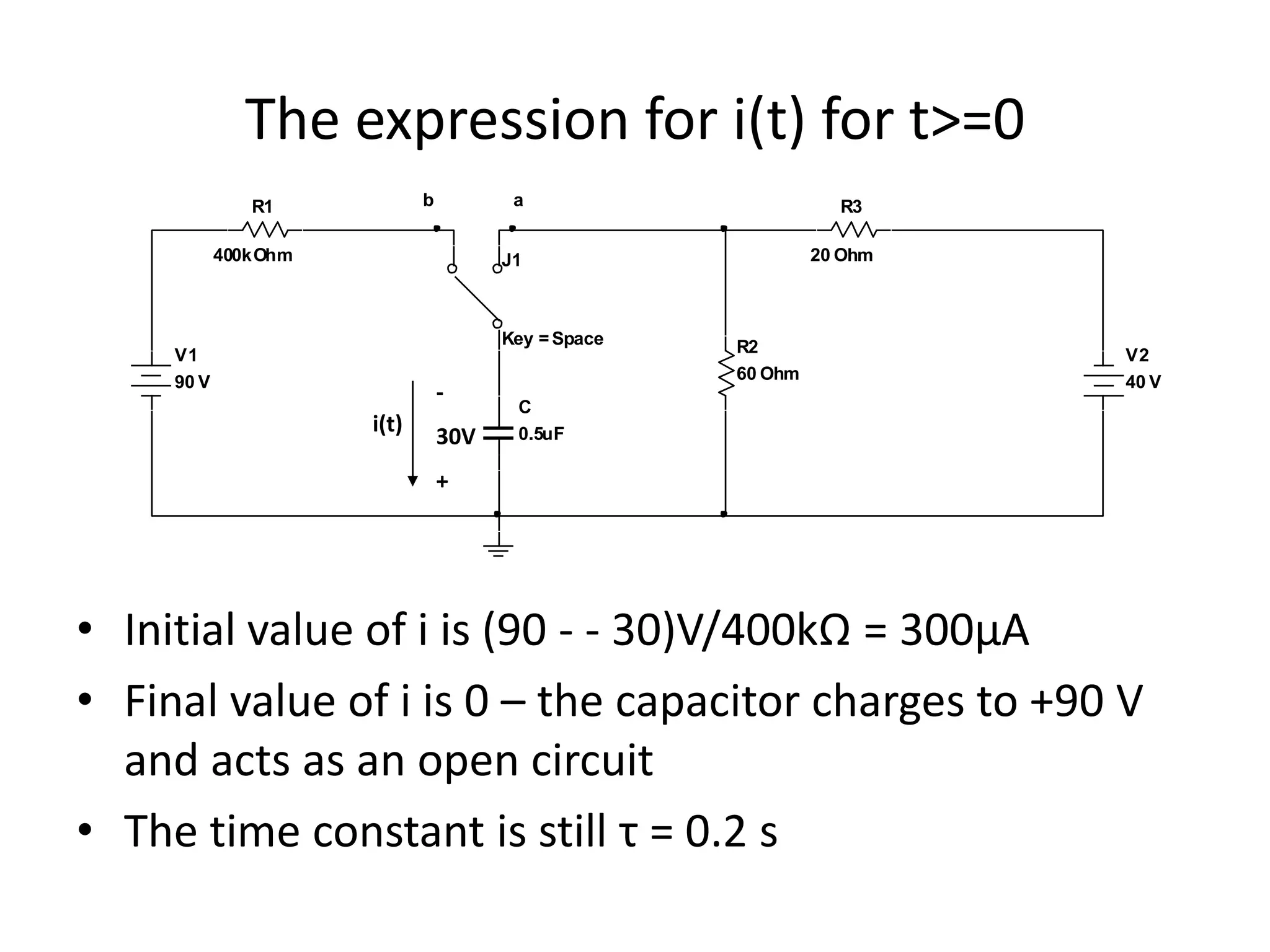
36. The expression for i(t) (continued)
t
i (t )
i( )
[ i (0 )
i ( )]e
t
i (t )
i (t )
0
[300 10
300 e
5t
A
6
0] e
0.2

37. How long after the switch is in position b does
the capacitor voltage equal 0?
vC (t )
120e
e
5t
90
5t
120e
5t
0
90
90
120
5t
ln
90
0 .2 8 7 6 8
120
t
0 .0 5 7 5 4 s
5 7 .5 4 m s

38. Plot vC(t)

39. Plot i(t)