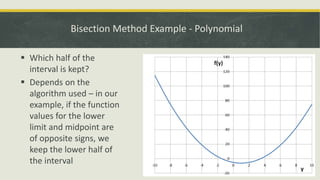
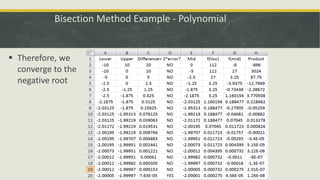
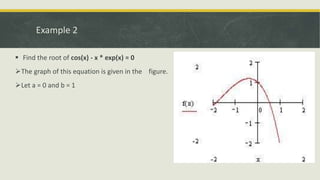
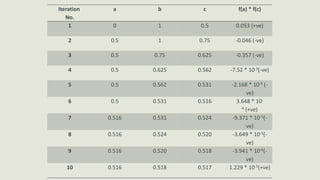
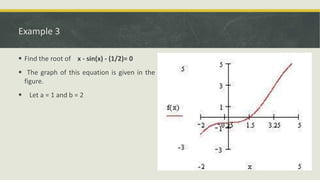
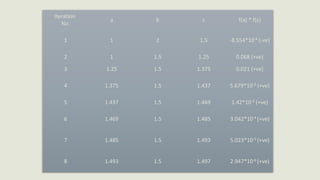
The document describes the bisection method for finding roots of equations. It provides an introduction to the bisection method and its graphical representation. It also presents the algorithm, a C program implementing the method, and examples finding roots of polynomial and trigonometric equations using bisection.

1. BISECTION METHOD
&
IT’S APPLICATIONS
A Presentation by:
150110120060: TIRTH PARMAR
150110120061: ABHIJIT TRIVEDI
150110120062: VAIBHAV SOLANKI
150110120063: NIRAV VASOYA

2. Topics to be Covered
 Introduction of Bisection method
 Graphical Representation Of Bisection Method
 Finding Roots of Equations
 Classification of Equations
 Algorithm
 Flowchart
 C program
 Examples

3. Finding Roots of Equations
• In this topic we are examining equations with one
independent variable.
• These equations may be linear or non-linear
• Non-linear equations may be polynomials or
generally non-linear equations
• A root of the equation is simply a value of the
independent variable that satisfies the equation

4. Classification of Equations
• Linear: independent variable appears to the first
power only, either alone or multiplied by a
constant
• Nonlinear:
– Polynomial: independent variable appears
raised to powers of positive integers only
– General non-linear: all other equations

5. BISECTION METHOD
 The bisection method in mathematics is a root-finding method that
repeatedly bisects an interval and then selects a subinterval in
which a root must lie for further processing.
 It is a very simple and robust method, but it is also relatively slow.
 Because of this, it is often used to obtain a rough approximation to
a solution which is then used as a starting point for more rapidly
converging methods.
 The method is also called “The Interval Halving Method”.

6. Graphical Representation Of Bisection Method
.

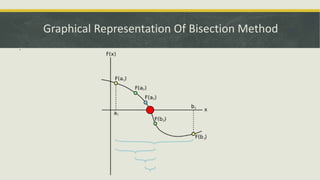
7.  The method is applicable for numerically solving the
equation f(x) = 0 for the real variable x, where f is a
continuous function defined on an interval [a, b] and
where f(a) and f(b) have opposite signs. In this case a and
b are said to bracket a root since, by the intermediate
value theorem, the continuous function f must have at
least one root in the interval (a, b).

8. C Program For Bisection Method
#include<stdio.h>
#include<conio.h>
# define eqn x*x-5
float f(float x)
{
float ans;
ans=eqn;
return(ans);}

9. Continue…
void main()
{
float a,b,x=0,x1=0;
int i=0;
printf("Enter the a and bn");
scanf("%f%f",&a,&b);
if(f(a)*f(b)>=0)
{
printf("The interval is wrongn");
getch();
return ;}

10. Continue...
do
{
x=(a+b)/2;
printf("ta=%f tb=%f tX%d=%f tf(x%d)=%fn",a,b,i,x,i,f(x));
if(x==x1)
{
printf("nnThe root is %fn",x);
break;
}
x1=x;

11. Continue...
i++;
if(f(a)*f(x)<0)
b=x;
else
a=x;
}while(f(a)-f(b)!=0.000);
printf("nThe final ans is %f",x);
getch();
}

12. Enter the a and b
2
2.5
a=2.000000 b=2.500000 X0=2.250000 f(x0)=0.062500
a=2.000000 b=2.250000 X1=2.125000 f(x1)=-0.484375
a=2.125000 b=2.250000 X2=2.187500 f(x2)=-0.214844
a=2.187500 b=2.250000 X3=2.218750 f(x3)=-0.077148
a=2.218750 b=2.250000 X4=2.234375 f(x4)=-0.007568
a=2.234375 b=2.250000 X5=2.242188 f(x5)=0.027405
a=2.234375 b=2.242188 X6=2.238281 f(x6)=0.009903
a=2.234375 b=2.238281 X7=2.236328 f(x7)=0.001163
Output of the Bisection Method

13. a=2.235962 b=2.236084 X12=2.236023 f(x8)=-0.000201
a=2.236023 b=2.236084 X13=2.236053 f(x9)=-0.000065
a=2.236053 b=2.236084 X14=2.236069 f(x10)=0.000003
a=2.236053 b=2.236069 X15=2.236061 f(x11)=-0.000031
a=2.236061 b=2.236069 X16=2.236065 f(x12)=-0.000014
a=2.236065 b=2.236069 X17=2.236067 f(x13)=-0.000005
a=2.236067 b=2.236069 X18=2.236068 f(x14)=-0.000001
a=2.236068 b=2.236069 X19=2.236068 f(x15)=0.000001
a=2.236068 b=2.236068 X20=2.236068 f(x16)=0.000000
The final ans is 2.236068
Continue…

14. Bisection Method Example - Polynomial
 Now consider this example:
 Use the bisection method, with allowed error of
0.0001

15. Bisection Method Example - Polynomial
 If limits of -10 to 0
are selected, the
solution converges
to x = -2

16. Bisection Method Example - Polynomial
 If limits of 0 to 10
are selected, the
solution converges
to x = 4

17. Bisection Method Example - Polynomial
 If limits of -10 to 10 are
selected, which root is
found?
 In this case f(-10) and f(10)
are both positive, and f(0) is
negative

18. Bisection Method Example - Polynomial
 Which half of the
interval is kept?
 Depends on the
algorithm used – in our
example, if the function
values for the lower
limit and midpoint are
of opposite signs, we
keep the lower half of
the interval

19. Bisection Method Example - Polynomial
 Therefore, we
converge to the
negative root

20. Example 2
 Find the root of cos(x) - x * exp(x) = 0
The graph of this equation is given in the figure.
Let a = 0 and b = 1

21. .
Iteration
No.
a b c f(a) * f(c)
1 0 1 0.5 0.053 (+ve)
2 0.5 1 0.75 -0.046 (-ve)
3 0.5 0.75 0.625 -0.357 (-ve)
4 0.5 0.625 0.562 -7.52 * 10-3(-ve)
5 0.5 0.562 0.531 -2.168 * 10-3 (-
ve)
6 0.5 0.531 0.516 3.648 * 10-
4 (+ve)
7 0.516 0.531 0.524 -9.371 * 10-5(-
ve)
8 0.516 0.524 0.520 -3.649 * 10-5(-
ve)
9 0.516 0.520 0.518 -3.941 * 10-6(-
ve)
10 0.516 0.518 0.517 1.229 * 10-5(+ve)

22. .
So one of the roots of cos(x) - x * exp(x) = 0 is
approximately 0.517

23. Example 3
 Find the root of x - sin(x) - (1/2)= 0
 The graph of this equation is given in the
figure.
 Let a = 1 and b = 2

24. Iteration
No.
a b c f(a) * f(c)
1 1 2 1.5 -8.554*10-4 (-ve)
2 1 1.5 1.25 0.068 (+ve)
3 1.25 1.5 1.375 0.021 (+ve)
4 1.375 1.5 1.437 5.679*10-3 (+ve)
5 1.437 1.5 1.469 1.42*10-3 (+ve)
6 1.469 1.5 1.485 3.042*10-4 (+ve)
7 1.485 1.5 1.493 5.023*10-5 (+ve)
8 1.493 1.5 1.497 2.947*10-6 (+ve)

25. .
 So one of the roots of x-sin(x)-(1/2) = 0 is
approximately 1.497.