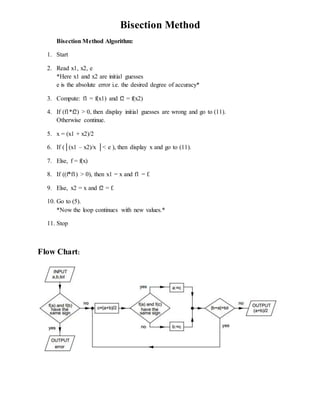
The bisection method is used to find the real roots of a nonlinear equation by iteratively narrowing down the interval where the root lies. It requires two initial guesses within an interval where the function changes sign. The method works by computing the midpoint of the interval and checking the sign of the function at that point, eliminating half of the interval and repeating until the interval size is less than a specified tolerance. The bisection method converges slowly but steadily and is guaranteed to find a root if given a valid initial interval.

1. Bisection Method
Bisection method is used to find the real roots of a nonlinear equation. The process is based on
the ‘Intermediate Value Theorem’. According to the theorem “If a function f(x) = 0 is continuous
in an interval (a, b), such that f (a) and f (b) are of opposite nature or opposite signs, then there
exists at least one or an odd number of roots between a and b.”
Bisection method is a closed bracket method and requires two initial guesses. It is the simplest
method with slow but steady rate of convergence. It never fails! The overall accuracy obtained is
very good, so it is more reliable in comparison to the Regula-Falsi method or the Newton-
Raphson method.
Features of Bisection Method:
 Type – closed bracket
 No. of initial guesses – 2
 Convergence – linear
 Rate of convergence – slow but steady
 Accuracy – good
 Programming effort – easy
 Approach – middle point

2. Bisection Method
Bisection Method Algorithm:
1. Start
2. Read x1, x2, e
*Here x1 and x2 are initial guesses
e is the absolute error i.e. the desired degree of accuracy*
3. Compute: f1 = f(x1) and f2 = f(x2)
4. If (f1*f2) > 0, then display initial guesses are wrong and go to (11).
Otherwise continue.
5. x = (x1 + x2)/2
6. If (│(x1 – x2)/x │< e ), then display x and go to (11).
7. Else, f = f(x)
8. If ((f*f1) > 0), then x1 = x and f1 = f.
9. Else, x2 = x and f2 = f.
10. Go to (5).
*Now the loop continues with new values.*
11. Stop
Flow Chart: