This document discusses key concepts about capacitors including:
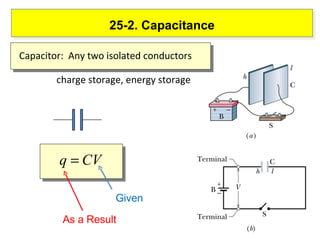
1) A capacitor is made of two conductors separated by an insulator. It can store an electric charge and energy.
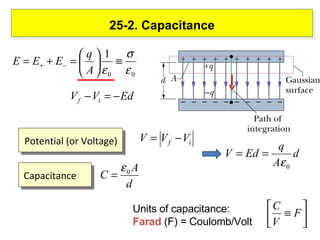
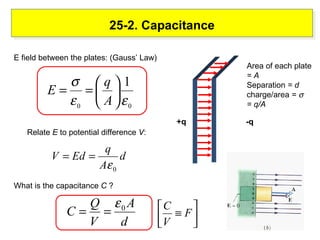
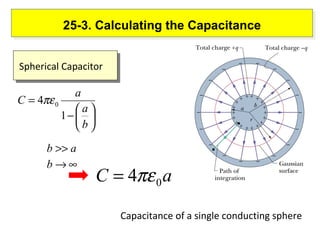
2) The capacitance of a capacitor depends on the geometry of the conductors and the dielectric material between them. It measures how much charge is stored for a given potential difference.
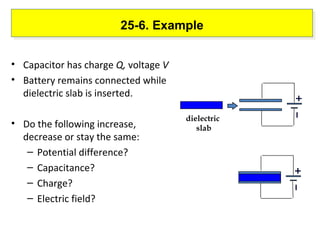
3) The energy stored in a capacitor depends on the charge and capacitance. Adding a dielectric increases the capacitance and stored energy.