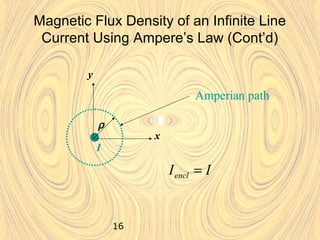
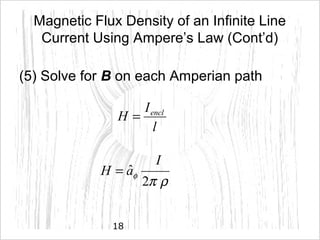
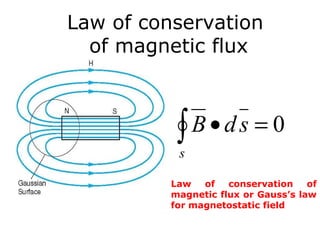
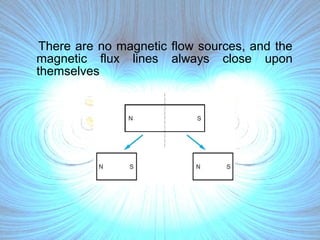
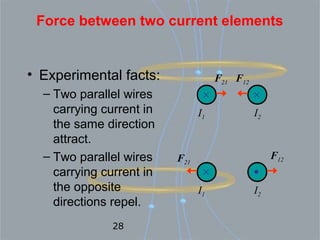
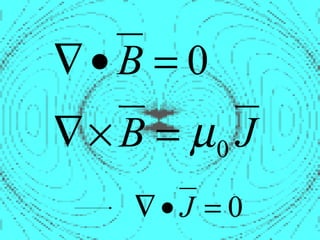Magnetostatic fields are produced when charges are moving with constant velocity, such as in a current-carrying wire. Biot-Savart's law states that the magnetic field produced by a current element is proportional to the current and inversely proportional to the distance from the element. Ampere's law, the integral form of which relates the line integral of magnetic field around a closed path to the current through the enclosed surface, can be used to determine the magnetic field produced by symmetric current distributions.

2. If charges are moving with constant velocity, a static
magnetic (or magnetostatic) field is produced. Thus,
magnetostatic fields originate from currents (for
instance,
direct currents in current-carrying wires).
Most of the equations we have derived for the electric
fields
may be readily used to obtain corresponding equations
for
magnetic fields if the equivalent analogous quantities
are
substituted.
2

3. Biot – Savart’s Law The magnetic field
intensity dH produced at
a point P by the
differential current
element Idl is
proportional to the
product of Idl and the
sine of the angle
between the element and
the line joining P to the
element and is inversely
proportional to the
square of the distance R
between P and the
element.
IN SI units, so,
α
2
sin
R
Idl
kdH
α=
2
R4
sinIdl
kdH
π
α
=
π
=
4
1
k
3

4. Using the definition of cross product
we can represent the previous equation in vector form as
The direction of can be determined by the right-hand rule
or by the right-handed screw rule.
If the position of the field point is specified by and the
position of the source point by
where is the unit vector directed from the source point to
the field point, and is the distance between these two
points.
)sin( nABaABBA θ=×
32
44 R
RdlI
R
adlI
Hd r
ππ
×
=
×
= RR = R
Rar =
r′
rre ′
rr ′−
r
32
4
)]([
4
)(
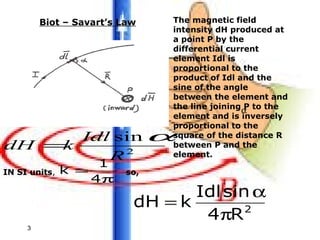
rr
rrdlI
rr
adlI
Hd r
′−
′−×
=
′−
×
=
ππ
Hd
MagnetostaticsMagnetostatics
4

5. The field produced
by a wire can be
found adding up
the fields produced
by a large number
of current elements
placed head to tail
along the wire (the
principle of
superposition).
MagnetostaticsMagnetostatics
5

6. 6
Types of Current Distributions
• Line current density (current) - occurs
for infinitesimally thin filamentary
bodies (i.e., wires of negligible
diameter).
• Surface current density (current per unit
width) - occurs when body is
perfectly conducting.
• Volume current density (current per unit
cross sectional area) - most general.

7. 7
Ampere’s Circuital Law in
Integral Form
• Ampere’s Circuit Law states that the line
integral of H around a closed path
proportional to the total current through
the surface bounding the path
enc
C
IldH =⋅∫

8. Ampere’s Circuital Law in
Integral Form (Cont’d)
By convention, dS is
taken to be in the
direction defined by the
right-hand rule applied
to dl.
∫ ⋅=
S
encl sdJI
Since volume current
density is the most
general, we can write
Iencl in this way.
S
dl
dS

9. 9
Applying Stokes’s Theorem to
Ampere’s Law
∫
∫∫
⋅==
⋅×∇=⋅
S
encl
SC
sdJI
sdHldH
⇒ Because the above must hold for any
surface S, we must have
JH =×∇ Differential form
of Ampere’s Law

10. 10
Ampere’s Law in Differential
Form
• Ampere’s law in differential form implies
that the B-field is conservative outside of
regions where current is flowing.

11. 11
Applications of Ampere’s Law
• Ampere’s law in integral form is an integral
equation for the unknown magnetic flux
density resulting from a given current
distribution.
encl
C
IldH =⋅∫
known
unknown

12. 12
Applications of Ampere’s Law
(Cont’d)
• In general, solutions to integral equations
must be obtained using numerical
techniques.
• However, for certain symmetric current
distributions closed form solutions to
Ampere’s law can be obtained.

13. 13
Applications of Ampere’s Law
(Cont’d)
• Closed form solution to Ampere’s law
relies on our ability to construct a suitable
family of Amperian paths.
• An Amperian path is a closed contour to
which the magnetic flux density is
tangential and over which equal to a
constant value.

14. 14
Magnetic Flux Density of an Infinite
Line Current Using Ampere’s Law
Consider an infinite line current along the z-
axis carrying current in the +z-direction:
I

15. 15
Magnetic Flux Density of an Infinite Line
Current Using Ampere’s Law (Cont’d)
(1) Assume from symmetry and the right-
hand rule the form of the field
(2) Construct a family of Amperian paths
φφ HaH ˆ=
circles of radius ρ where
∞≤≤ ρ0

16. 16
Magnetic Flux Density of an Infinite Line
Current Using Ampere’s Law (Cont’d)
Amperian path
IIencl =
I
ρ
x
y

17. 17
Magnetic Flux Density of an Infinite Line
Current Using Ampere’s Law (Cont’d)
(4) For each Amperian path, evaluate the
integral
HlldH
C
=⋅∫
ρπφ 2HldH
C
=⋅∫
magnitude of H
on Amperian
path.
length
of Amperian
path.

18. 18
Magnetic Flux Density of an Infinite Line
Current Using Ampere’s Law (Cont’d)
(5) Solve for B on each Amperian path
l
I
H encl
=
ρπ
φ
2
ˆ
I
aH =

19. Magnetic Flux Density
The magnetic flux density vector is related to the magnetic
field intensity by the following equation
T (tesla) or Wb/m2
where is the permeability of the medium. Except for
ferromagnetic materials ( such as cobalt, nickel, and iron),
most materials have values of very nearly equal to that for
vacuum,
H/m (henry per meter)
The magnetic flux through a given surface S is given by
Wb (weber)
H
,HB µ=
µ
7
o 104 −
⋅π=µ
∫ ⋅=Ψ
S
,sdB
µ
19

20. 0=•∫s
sdB
Law of conservation
of magnetic flux
Law of conservation of
magnetic flux or Gauss’s law
for magnetostatic field

21. JB
B
0
0
µ=×∇
=•∇
0=•∇ J

22. There are no magnetic flow sources, and the
magnetic flux lines always close upon
themselves

23. 23
Forces due to magnetic field
There are three ways in which force due to magnetic fields can
be experienced
1.Due to moving charge particle in a B field
2.On a current element in an external field
3.Between two current elements

24. The force is perpendicular to the direction of charge motion,
and is also perpendicular to .
Force on a Moving Charge
• A moving point charge placed in a
magnetic field experiences a force
given by
BvQ
The force experienced
by the point charge is
in the direction into the
paper.
B
BuqFm ×=

25. BuqF
EqF
m
e
×=
= FFF me =+
)( BuEqF ×+=
Lorentz’s Force equation
Note: Magnetic force is zero for q moving in the
direction of the magnetic field (sin0=0)
If a point charge is moving in a region where both
electric and magnetic fields exist, then it experiences a
total force given by

26. Magnetic Force on a current element
One can tell if a magneto-static field is present because it
exerts forces on moving charges and on currents. If a
current
element is located in a magnetic field , it experiences a
force
This force, acting on current element , is in a direction
perpendicular to the current element and also perpendicular
to . It is largest when and the wire are perpendicular.
Idl B
dF=Idl×B
B
Idl
B
26
__
uQlId ⇔

27. 27
FORCE ON A CURRENT ELEMENT
• The total force exerted on a circuit C
carrying current I that is immersed in a
magnetic flux density B is given by
∫ ×=
C
BldIF

28. 28
• Experimental facts:
– Two parallel wires
carrying current in
the same direction
attract.
– Two parallel wires
carrying current in
the opposite
directions repel.
× ×
I1 I2
F12F21
× •
I1 I2
F12F21
Force between two current elements

29. 29
• Experimental facts:
– A short current-
carrying wire
oriented
perpendicular to a
long current-
carrying wire
experiences no
force.
×
I1
F12 = 0
I2
Force between two current elements

30. 30
• Experimental facts:
– The magnitude of the force is inversely
proportional to the distance squared.
– The magnitude of the force is proportional to
the product of the currents carried by the two
wires.
Force between two current elements

31. 31
• The force acting on a current element I2dl2
by a current element I1dl1 is given by
( )
2
12
11220
12
12
ˆ
4
)(
R
aldIldI
Fdd
R××
=
π
µ
Permeability of free space
µ0 = 4π × 10-7
F/m
Force between two current elements

32. 32
• The total force acting on a circuit C2 having
a current I2 by a circuit C1 having current I1
is given by
( )
∫ ∫
××
=
2 1
12
2
12
12210
12
ˆ
4 C C
R
R
aldldII
F
π
µ
Force between two current elements

33. 33
• The force on C1 due to C2 is equal in
magnitude but opposite in direction to the
force on C2 due to C1.
1221 FF −=
Force between two current elements

34. EEL 3472EEL 347234