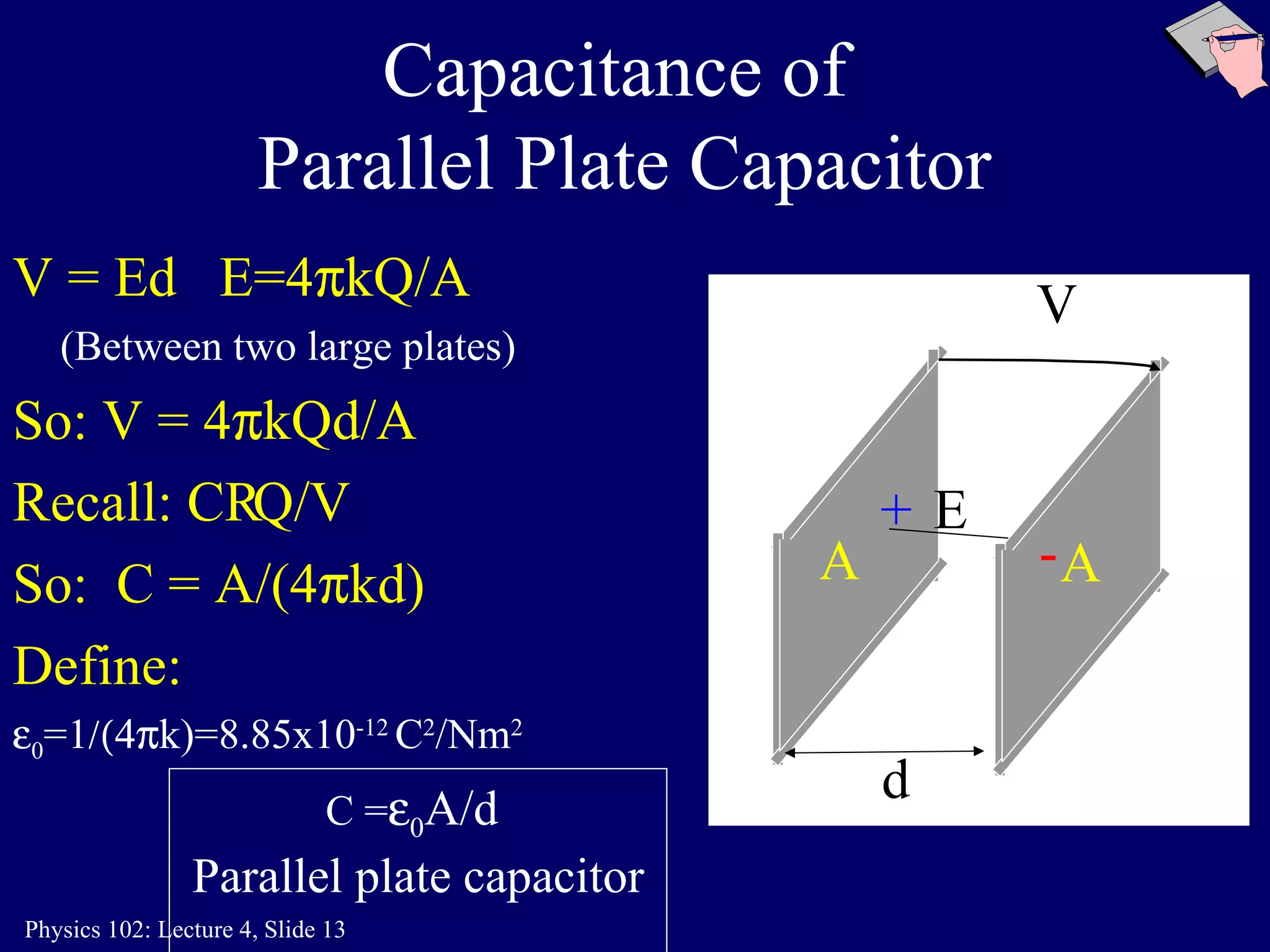
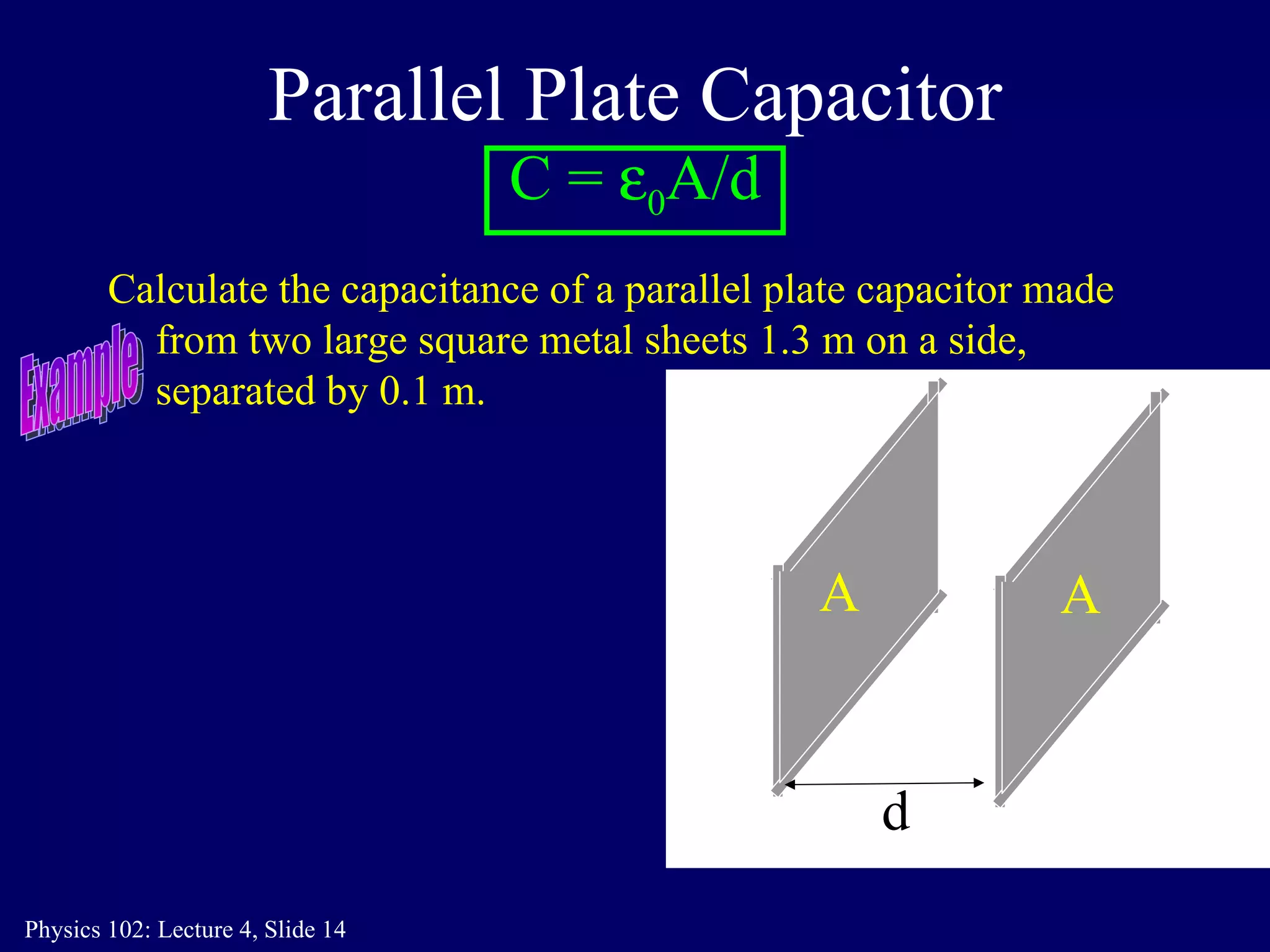
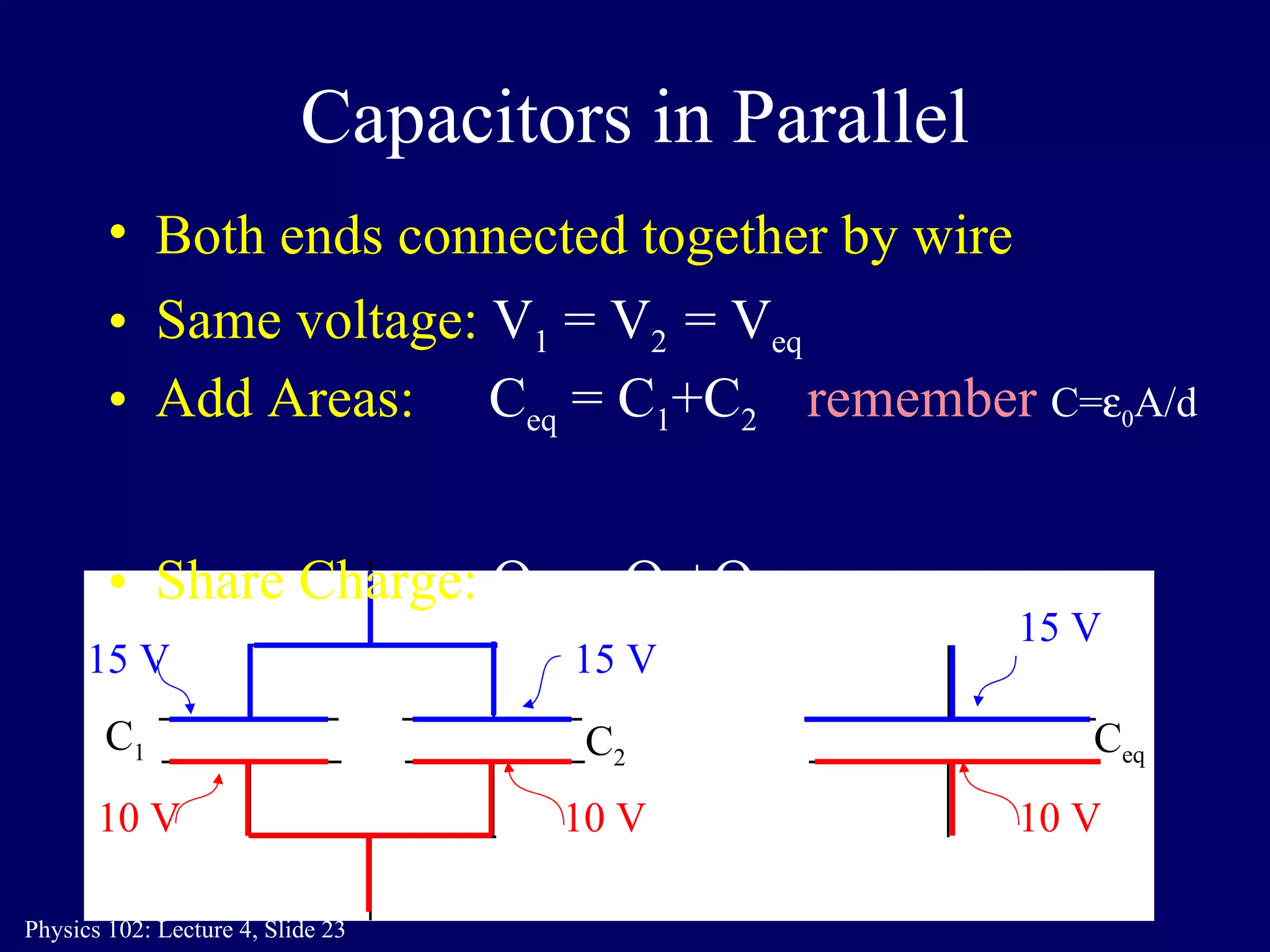
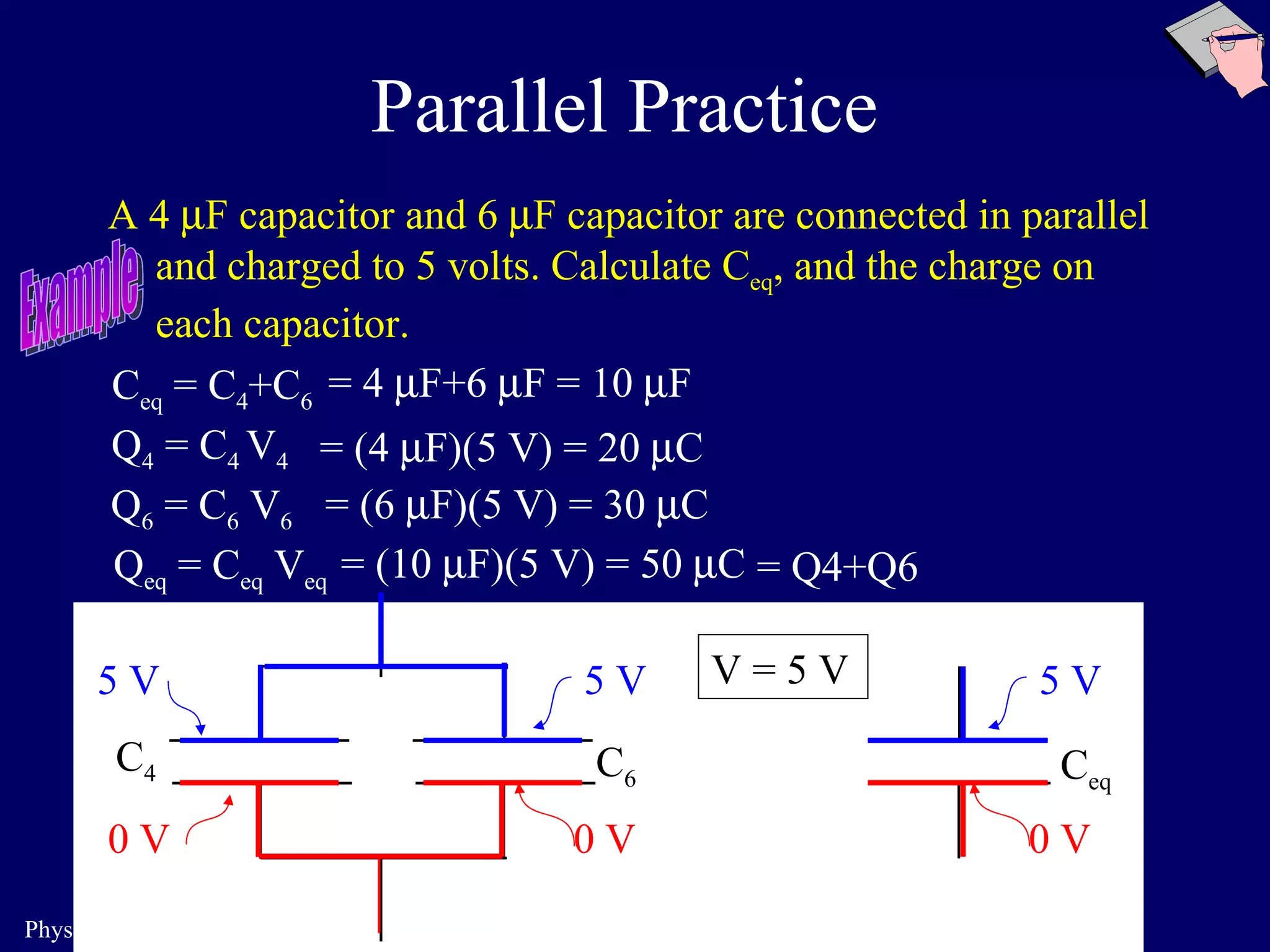
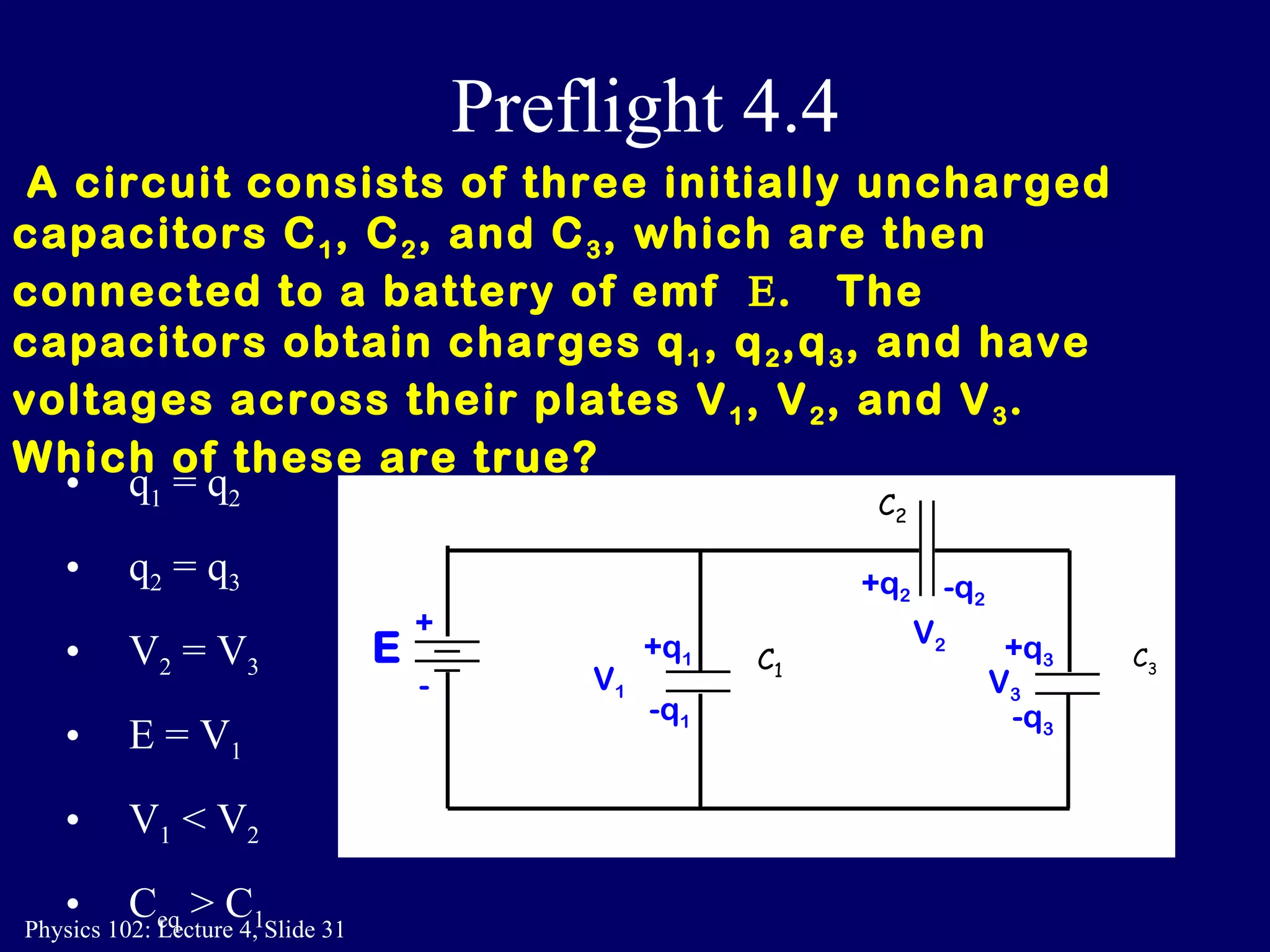
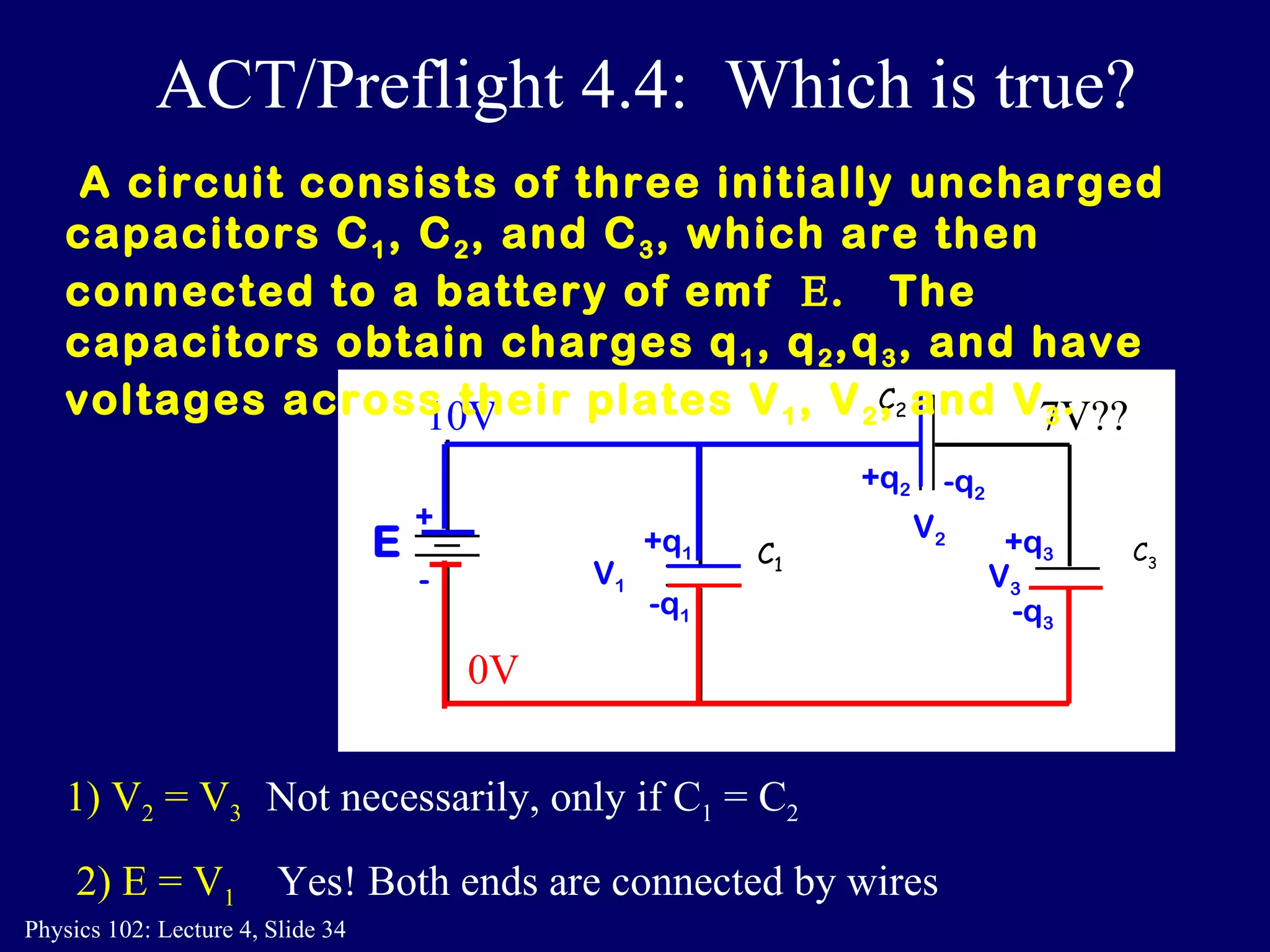
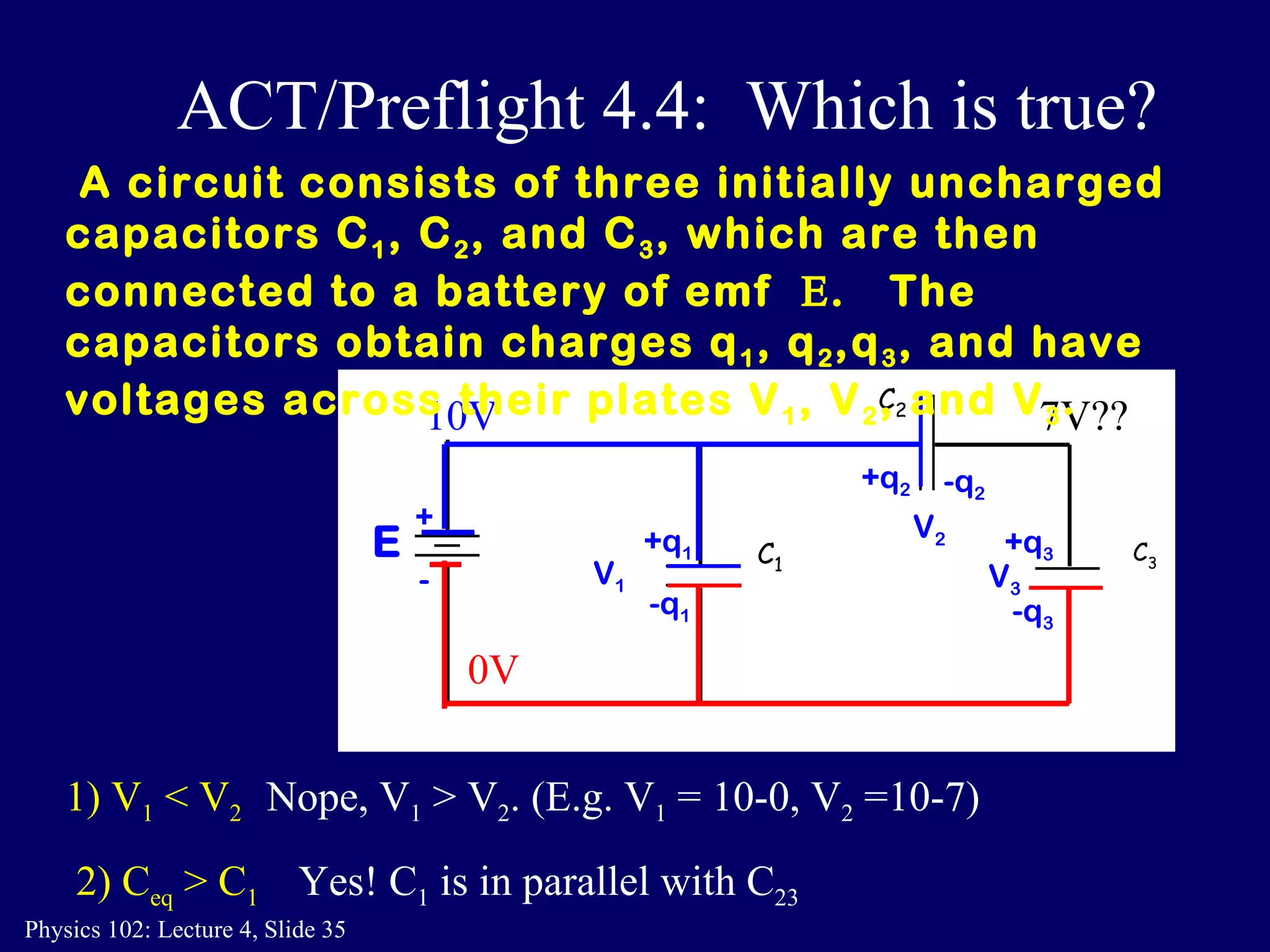
1. The document discusses capacitors and capacitance, including parallel plate capacitors. It defines capacitance as the ability to store separated charge. 2. For a parallel plate capacitor, the capacitance is given by C = ε0A/d, where ε0 is the permittivity of free space, A is the plate area, and d is the plate separation. 3. Capacitors can be connected in parallel or in series. For capacitors in parallel, the total capacitance is the sum of the individual capacitances. For capacitors in series, the total capacitance is given by 1/(1/C1 + 1/C2).

1. Capacitors Physics 102: Lecture 04

2. Recall from last lecture….. Electric Fields, Electric Potential

3. Comparison: Electric Potential Energy vs. Electric Potential  V AB : the difference in electric potential between points B and A  U AB : the change in electric potential energy of a charge q when moved from A to B  U AB = q  V AB q A B

5. Electric Potential: Summary E field lines point from higher to lower potential For positive charges, going from higher to lower potential is “downhill” For a battery, the (+) terminal is at a higher potential than the (–) terminal Positive charges tend to go “downhill”, from + to  Negative charges go in the opposite direction, from  to +  U AB = q  V AB

6. Important Special Case Uniform Electric Field + + + + + - - - - - Two large parallel conducting plates of area A +Q on one plate  Q on other plate Then E is uniform between the two plates: E=4  kQ/A zero everywhere else This result is independent of plate separation This is call a parallel plate capacitor

7. Parallel Plate Capacitor: Potential Difference E=E 0 d V =V A – V B = +E 0 d + + + + + - - - - - A B d + + + + + - - - - - + + + + + - - - - - E=2 E 0 V =V A – V B = +2E 0 d Potential difference is proportional to charge: Double Q  Double V Charge Q on plates Charge 2Q on plates E 0 =4  kQ/A A B

9. Capacitance: The ability to store separated charge C  Q/V Any pair conductors separated by a small distance. (e.g. two metal plates) Capacitor stores separated charge Positive Q on one conductor, negative Q on other Net charge is zero Q=CV U =(½) Q V Stores Energy Units: 1 Coulomb/Volt = 1 Farad (F) E d + + + + + - - - - -

10. Why Separate Charge? Camera Flash Defibrillator—see ex. 17.12 in text AC -> DC Tuners Radio Cell phones Analogy to a waterfall

11. Capacitance Practice How much charge is on a 0.9 F capacitor which has a potential difference of 200 Volts? How much energy is stored in this capacitor? Example

13. Capacitance of Parallel Plate Capacitor V = Ed E=4  kQ/A (Between two large plates) So: V = 4  kQd/A Recall: C  Q/V So: C = A/(4  kd) Define:  0 =1  k)=8.85x10 -12 C 2 /Nm 2 A d A E + - V C =  0 A/d Parallel plate capacitor

14. Parallel Plate Capacitor C =  0 A/d Calculate the capacitance of a parallel plate capacitor made from two large square metal sheets 1.3 m on a side, separated by 0.1 m. A d A Example

15. Dielectric Placing a dielectric between the plates increases the capacitance. C =  C 0 Capacitance with dielectric Dielectric constant (  > 1) Capacitance without dielectric

17. A parallel plate capacitor given a charge q. The plates are then pulled a small distance further apart. What happens to the charge q on each plate of the capacitor? ACT: Parallel Plates 1) Increases 2) Constant 3) Decreases Remember charge is real/physical. There is no place for the charges to go. +q -q + + + + - - - - d pull pull

18. A parallel plate capacitor given a charge q. The plates are then pulled a small distance further apart. Which of the following apply to the situation after the plates have been moved? 1)The capacitance increases True False 2)The electric field increases True False 3)The voltage between the plates increases True False Preflight 4.1 +q -q + + + + - - - - d pull pull

19. A parallel plate capacitor given a charge q. The plates are then pulled a small distance further apart. Which of the following apply to the situation after the plates have been moved? ACT/Preflight 4.1 The energy stored in the capacitor A) increases B) constant C) decreases +q -q + + + + - - - - d pull pull

21. Two identical parallel plate capacitors are shown in end-view in A) of the figure. Each has a capacitance of C. A ) B ) If the two are joined as in (B) of the figure, forming a single capacitor, what is the final capacitance? 1) 2C 2) C 3) C/2 ACT/Preflight 4.2

22. Voltage in Circuits Elements are connected by wires. Any connected region of wire has the same potential. V C 1 = 5-0 V= 5 V V C 3 = 15-12 V= 3 V V C 2 = 12-5 V= 7 V C 1 C 2 C 3 Example The potential difference across an element is the element’s “voltage.” V wire 1 = 0 V V wire 2 = 5 V V wire 3 = 12 V V wire 4 = 15 V

23. Capacitors in Parallel Both ends connected together by wire C 1 C 2 15 V 10 V 15 V 10 V Add Areas: C eq = C 1 +C 2 remember C=  0 A/d Share Charge: Q eq = Q 1 +Q 2 = V eq Same voltage: V 1 = V 2 C eq 15 V 10 V

25. Parallel Practice A 4  F capacitor and 6  F capacitor are connected in parallel and charged to 5 volts. Calculate C eq , and the charge on each capacitor. C 4 C 6 C eq 5 V 0 V 5 V 0 V 5 V 0 V C eq = C 4 +C 6 Q 4 = C 4 V 4 Q 6 = C 6 V 6 Q eq = C eq V eq = 4  F+6  F = 10  F = (4  F)(5 V) = 20  C = (6  F)(5 V) = 30  C = (10  F)(5 V) = 50  C = Q4+Q6 V = 5 V Example

26. Capacitors in Series Connected end-to-end with NO other exits Same Charge: Q 1 = Q 2 = Q eq Add d: C 1 C 2 + + + + + + + + + + + + + - + - + - +Q -Q Share Voltage: V 1 +V 2 =V eq C eq - + - + +Q -Q +Q -Q

27. Series Practice A 4  F capacitor and 6  F capacitor are connected in series and charged to 5 volts. Calculate C eq , and the charge on the 4  F capacitor . C eq C 4 C 6 + - + - 5 V 0 V Q = CV Example + - +Q -Q +Q -Q +Q -Q 5 V 0 V

29. Comparison: Series vs. Parallel Series Can follow a wire from one element to the other with no branches in between. Parallel Can find a loop of wire containing both elements but no others (may have branches). C 1 C 2 C 2 C 1

30. Electromotive Force Battery Maintains constant potential difference V Does NOT produce or supply charges, just “pushes” them. + -

31. Preflight 4.4 A circuit consists of three initially uncharged capacitors C 1 , C 2 , and C 3 , which are then connected to a battery of emf  . The capacitors obtain charges q 1 , q 2 ,q 3 , and have voltages across their plates V 1 , V 2 , and V 3 . Which of these are true? q 1 = q 2 q 2 = q 3 V 2 = V 3 E = V 1 V 1 < V 2 C eq > C 1 C 2 C 3 C 1 E + - -q 2 +q 1 -q 1 +q 3 -q 3 +q 2 V 1 V 2 V 3

33. A circuit consists of three initially uncharged capacitors C 1 , C 2 , and C 3 , which are then connected to a battery of emf  . The capacitors obtain charges q 1 , q 2 ,q 3 , and have voltages across their plates V 1 , V 2 , and V 3 . 1) q 1 = q 2 Not necessarily C 1 and C 2 are NOT in series. 2) q 2 = q 3 Yes! C 2 and C 3 are in series. ACT/Preflight 4.4: Which is true? C 2 C 3 C 1 E + - -q 2 +q 1 -q 1 +q 3 -q 3 +q 2 V 1 V 2 V 3

34. 1) V 2 = V 3 Not necessarily, only if C 1 = C 2 2) E = V 1 Yes! Both ends are connected by wires A circuit consists of three initially uncharged capacitors C 1 , C 2 , and C 3 , which are then connected to a battery of emf  . The capacitors obtain charges q 1 , q 2 ,q 3 , and have voltages across their plates V 1 , V 2 , and V 3 . ACT/Preflight 4.4: Which is true? C 2 C 3 C 1 E + - -q 2 +q 1 -q 1 +q 3 -q 3 +q 2 V 1 V 2 V 3 10V 0V 7V??

35. 1) V 1 < V 2 Nope, V 1 > V 2 . (E.g. V 1 = 10-0, V 2 =10-7) 2) C eq > C 1 Yes! C 1 is in parallel with C 23 A circuit consists of three initially uncharged capacitors C 1 , C 2 , and C 3 , which are then connected to a battery of emf  . The capacitors obtain charges q 1 , q 2 ,q 3 , and have voltages across their plates V 1 , V 2 , and V 3 . ACT/Preflight 4.4: Which is true? C 2 C 3 C 1 E + - -q 2 +q 1 -q 1 +q 3 -q 3 +q 2 V 1 V 2 V 3 10V 0V 7V??

36. Capacitance C = Q/V Parallel Plate: C =  0 A/d Capacitors in parallel: C eq = C 1 +C 2 Capacitors in series: C eq = 1/(1/C 1 +1/C 2 ) Batteries provide fixed potential difference Recap of Today’s Lecture