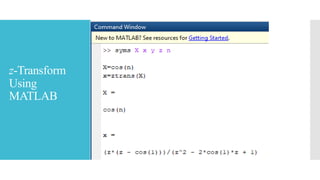
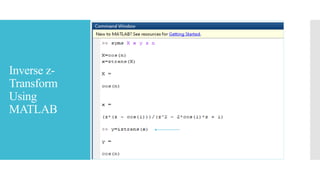
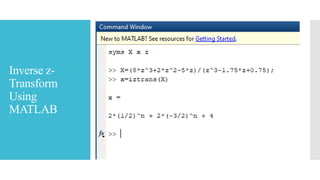
This document discusses the z-transform, which is a mathematical tool used to analyze discrete-time control systems. The z-transform plays a similar role for discrete systems as the Laplace transform does for continuous systems. The document covers the definition of the z-transform, its region of convergence in the z-plane, methods for taking the inverse z-transform, properties of the z-transform, and how to use MATLAB for z-transforms.

2. Z-Transform

3. Presented by:
 Ayman Dilshad EE161022
 Hasnain Yaseen EE161021

4. CONTENTS:
1. Z-Transform
2. Commands in MATLAB
3. Convergence Region of Z-transform
4. The Inverse Z-Transform
5. Methods of finding Inverse Z-transform
6. Z-transform pairs
7. Properties of the z-Transform
8. z-Transform Using MATLAB

5. Z-Transform
 The z transform is a mathematical tool commonly used
for the analysis and synthesis of discrete-time control
systems.
 For discrete-time systems, z-transforms play the same
role as Laplace transforms do in continuous-time
systems

6. Continue…
 Most general concept for transformation of discrete
time series

7. The z-
Transform
Definition

8. Bilateral vs.
Unilateral
Two sided or bilateral z-transform
 Unilateral z-transform
   




n
n
znxzX
   




0n
n
znxzX

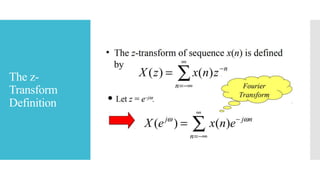
9. Z-Transform
 Bilateral Forward z-transform
 Bilateral Inverse z-transform
 




n
n
znhzH )(



R
n
dzzzH
j
nh 1
)(
2
1
][


10. Commands in
MATLAB
 Z-Transforms
 Inverse Z-Transform

11. Convergence
Region of Z-
transform
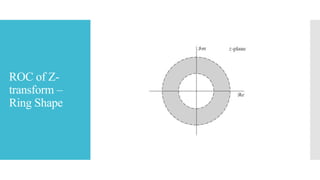
Region of convergence (ROC)
 Since the z-transform can be interpreted as the Fourier
transform of the product of the original sequence x[n]
and the exponential sequence r-n, it is possible for the z-
transform to converge even if the Fourier transform does
not.
 Because
 X(z) is convergent (i.e. bounded) i.e., Σx[n]r-n <∞, if x[n]
is absolutely summable.
     







n
n
n
n
znxznxzX

12. Continue..
 Eg., x[n] = u[n] is absolutely summable if r>1. This
means that the z-transform for the unit step exists with
ROC |z|>1.
 In fact, convergence of the power series X(z) depends
only on |z|.
 If some value of z, say z = z1, is in the ROC, then all
values of z on the circle defined by |z|=| z1| will also be
in the ROC.
 Thus the ROC will consist of a ring in the z-plane.
  



n
n
znx

13. ROC of Z-
transform –
Ring Shape

14. The Inverse Z-
Transform
 Inverse z-transform is opposite of z-transform.
 For discrete-time systems, Inverse z-transforms play the
same role as Inverse Laplace transforms do in
continuous-time systems.

15. The Inverse Z-
Transform
• Most general concept for inverse transformation of discrete time series

16. Methods of
finding Inverse
Z-transform
 There are generally three methods of inverse z-
transform
I. Synthetic division method
II. Partial fraction expansion
III. Power series expansion

17. Z-transform
pairs

18. Properties of
the z-
Transform

19. z-Transform
Using
MATLAB

20. Inverse z-
Transform
Using
MATLAB

21. Inverse z-
Transform
Using
MATLAB

22. Advantages of
z-transform
 Stability of LTI system can be determined using z-
transform.
 By calculating z-transform of a given signal, Discrete
Fourier Transform (DFT) and Fourier Transform (FT)
can be determined.
 The solution of differential equations can be simplified
using z-transform.