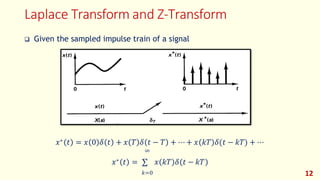
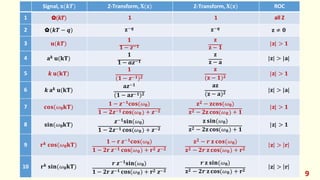
The document discusses the inverse z-transform in digital signal processing (DSP), contrasting difference equations with differential equations, and emphasizing the utility of z-transforms in solving linear time-invariant (LTI) systems. It details the method for obtaining the inverse z-transform via long division, partial fraction expansion, and other techniques, including examples illustrating these methods. Additionally, it provides comparisons between the Laplace transform and z-transform, clarifying their respective roles in continuous and discrete time analysis.