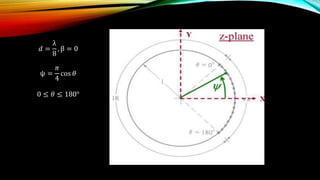
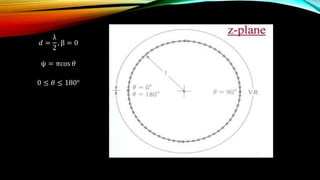
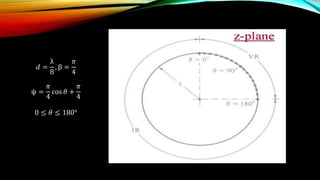
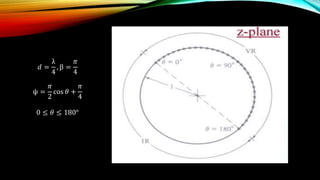
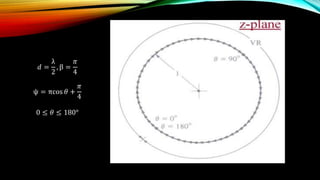
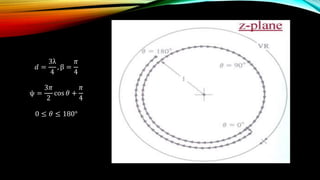
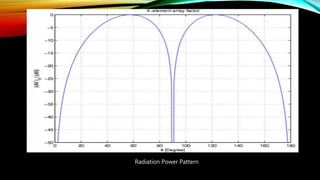
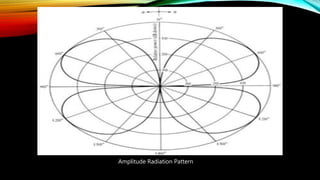
The document discusses the Schelkunoff polynomial method for antenna synthesis. It involves designing an antenna array to produce a desired radiation pattern with nulls in specific directions. The method models the array factor as a polynomial and solves for the roots, which correspond to null locations. Array coefficients are then determined to produce the required roots within the visible region of the unit circle based on the element spacing and progressive phase shifts. As an example, a 4 element linear array is designed with nulls at 0, 90, and 180 degrees.

1. SCHELKUNOFF
POLYNOMIAL METHOD
Swapnil Bangera
(ME-EXTC)

2. OVERVIEW
• What is antenna synthesis?
• Steps involved in antenna synthesis
• Various methods of antenna synthesis
• Schelkunoff Polynomial Method
• Design Technique
• Design Steps
• Design example

3. ANTENNA SYNTHESIS
• In general, analysis of antenna is done by selecting a particular antenna model and
its various radiation characteristics such as pattern, directivity, impedance,
beamwidth, efficiency, polarization, and bandwidth are analysed using standard
procedures usually by specifying its current distribution.
• In practice, it is often necessary to design an antenna system that will yield desired
radiation characteristics. Common requests to design an antenna are for pattern to
exhibit a desired distribution, beamwidth, size of side lobes, minor lobes, etc.
• The task, in general, is to find not only the antenna configuration but also its
geometrical dimensions and excitation distribution.

4. • The designed system should yield, either exactly or approximately, an acceptable
radiation pattern.
• This method of design is known as antenna synthesis.

5. ANTENNA SYNTHESIS STEPS
• Antenna synthesis usually requires that first an approximate analytical model is
chosen to represent, either exactly or approximately, the desired pattern.
• The second step is to match the analytical model to a physical antenna model.

6. ANTENNA SYNTHESIS METHODS
Antenna synthesis can be classified into three categories:
One group requires that the antenna patterns possess nulls in desired directions.
 Schelkunoff Polynomial Method
Another category requires that the patterns exhibit a desired distribution in the entire visible
region. This is referred to as beam shaping.
 Fourier Transform Method
 Woodward Lawson Method
Third group includes techniques that produce patterns with narrow beams and low side
lobes.
 Binomial Method
 Dolph-Tschebscheff Method
 Taylor line-source

7. SCHELKUNOFF POLYNOMIAL
METHOD
• Schelkunoff polynomial method is conductive to the synthesis of arrays whose
patterns possess nulls in desired directions.
• To complete the design, this method requires information on the number of nulls
and their locations.
• The number of elements and their excitation coefficients are then derived.

8. DESIGN TECHNIQUE
• The array factor for an N-element, equally spaced, non-uniform amplitude, and
progressive-phase excitation is given by:
AF = 𝑛=1
𝑁
𝑎 𝑛 𝑒 𝑗(𝑛−1)(𝑘𝑑 cos θ+ β) = 𝑛=1
𝑁
𝑎 𝑛 𝑒 𝑗(𝑛−1)ψ.........(1)
where 𝑎 𝑛 accounts for the non-uniform amplitude excitation of each
element. The spacing between the elements is 𝑑 and β is the progressive
phase shift
• Letting
𝑧 = 𝑥 + 𝑗𝑦 = 𝑒 𝑗ψ = 𝑒 𝑗(𝑘𝑑𝑐𝑜𝑠𝜃+ 𝛽).........(2)
• Rewriting (1) as
AF = 𝑛=1
𝑁
𝑎 𝑛 𝑧 𝑛−1
= 𝑎1 + 𝑎2 𝑧 + 𝑎3 𝑧2
+ … + 𝑎 𝑁 𝑧 𝑁−1
…......(3)

9. which is a polynomial of degree (𝑁 − 1). From the mathematics of
complex variables and algebra, any polynomial of degree 𝑁 − 1 has
(𝑁 − 1) roots and can be expressed as a product of 𝑁 − 1 linear terms.
Thus we can write (3) as
AF = 𝑎 𝑛 𝑧 − 𝑧1 𝑧 − 𝑧2 𝑧 − 𝑧3 … 𝑧 − 𝑧 𝑁−1 .........(4)
where 𝑧1, 𝑧2, 𝑧3, … , 𝑧 𝑁−1 are the roots, which may be complex, of the
polynomial
• The magnitude of (4) can ne expresses as
𝐴𝐹 = 𝑎 𝑛 𝑧 − 𝑧1 𝑧 − 𝑧2 𝑧 − 𝑧3 … 𝑧 − 𝑧 𝑁−1 ………(5)
• The complex variable 𝑧 of (2) can be written in another form as
𝑧 = 𝑧 𝑒 𝑗ψ
= 𝑧 < ψ.........(6)
ψ = 𝑘𝑑 cos 𝜃 + 𝛽………(7)
It is clear that for any value of 𝑑, 𝜃, and 𝛽 the magnitude of 𝑧 lies always on a unit
circle; however its phase depends upon 𝑑, 𝜃, and 𝛽. For 𝛽 = 0, lets plot the value of z,
magnitude and phase, as 𝜃 takes values of 0 to π rad.

10. 𝑑 =
λ
8
, β = 0
ψ =
𝜋
4
cos 𝜃
0 ≤ 𝜃 ≤ 180°

11. 𝑑 =
λ
4
, β = 0
ψ =
𝜋
2
cos 𝜃
0 ≤ 𝜃 ≤ 180°

12. 𝑑 =
λ
2
, β = 0
ψ = πcos 𝜃
0 ≤ 𝜃 ≤ 180°

13. 𝑑 =
3λ
4
, β = 0
ψ =
3𝜋
2
cos 𝜃
0 ≤ 𝜃 ≤ 180°

14. • For all the physically observable angles of θ, only exists over a part of the circle.
• Any values of z outside that arc are not realizable by any physical observation angle
θ for the spacing.
• The realizable part of the circle is referred to as the visible region and the remaining
as invisible region.
• It is obvious that the visible region can be extended by increasing the spacing
between the elements.
• It requires a spacing of at least λ
2 to encompass, at least once, the entire circle. Any
spacing greater than λ
2 leads to multiple values of z.

15. • To demonstrate the versatility of the arrays, let us plot the values of z for the same
spacings but with a 𝛽 = 𝜋
4.

16. 𝑑 =
λ
8
, β =
𝜋
4
ψ =
𝜋
4
cos 𝜃 +
𝜋
4
0 ≤ 𝜃 ≤ 180°

17. 𝑑 =
λ
4
, β =
𝜋
4
ψ =
𝜋
2
cos 𝜃 +
𝜋
4
0 ≤ 𝜃 ≤ 180°

18. 𝑑 =
λ
2
, β =
𝜋
4
ψ = πcos 𝜃 +
𝜋
4
0 ≤ 𝜃 ≤ 180°

19. 𝑑 =
3λ
4
, β =
𝜋
4
ψ =
3𝜋
2
cos 𝜃 +
𝜋
4
0 ≤ 𝜃 ≤ 180°

20. • A comparison between the corresponding figures indicates that the overall visible
region for each spacing has not changed but its relative position on the unit circle
has rotated counter clockwise by an amount equal to β.
• We can conclude that the overall extent of the visible region can be controlled by
the spacing between the elements and its relative position on the unit circle by the
progressive phase excitation of the elements.
• These two can be used effectively in the design of the array factors.

21. • To demonstrate all the principles, lets consider an example along with some
computations.
Roots of array factor Roots of array factor on unit circle
and within visible region

22. • If all the roots are located in the visible region of the unit circle, then each one
corresponds to a null in the pattern of 𝐴𝐹 because as θ changes z changes and
eventually passes through each of the 𝑧 𝑛’s.
• When all the zeros (roots) are not in the visible region of the unit circle, then only
those zeroes on the visible region will contribute to the nulls of the pattern.
• If no zeros exist in the visible region of the unit circle, then that particular array
factor has no nulls for any value of θ.
• However, if a given zero lies on the unit circle but not in its visible region, that zero
can be included in the pattern by changing the phase excitation 𝛽 so that the visible
region is rotated until it encompasses that root.

23. DESIGN STEPS
1. For given spacing, phase shift and null locations plot the visible region.
2. Find the roots of AF corresponding to the desired null locations.
3. Check whether the roots lie on the unit circle within the visible region.
4. Find the array factor with respect to the roots present on the unit circle within the
visible region.
5. Find array coefficients

24. EXAMPLE
• Design a linear array with a spacing between the elements of 𝑑 = λ
4 such that it has
zeros at 𝜃 = 0°, 90°, 𝑎𝑛𝑑 180°. Determine the number of elements, their excitation,
and plot the derived pattern.
ψ =
2𝜋
λ
× 𝑑 cos 𝜃 + 𝛽
𝑧 = 1 < ψ
𝐴𝐹 = 𝑧 − 𝑧1 𝑧 − 𝑧2 𝑧 − 𝑧3 … (𝑧 − 𝑧 𝑁−1)
Array Coefficients 𝑎1, 𝑎2, 𝑎3, … , 𝑎 𝑁

25. Radiation Power Pattern

26. Amplitude Radiation Pattern