This document is the cover page for a mathematics preliminary examination. It provides instructions for candidates taking the exam, including writing their identification information, answering all questions, showing necessary work, using calculators appropriately, and specifying the degree of accuracy for answers. It also lists several mathematical formulas that may be useful for the exam, such as formulas for compound interest, mensuration, trigonometry, and statistics. The total number of marks for the exam is 80.

1. ANDERSON SECONDARY SCHOOL
2009 Preliminary Examination
Secondary Four Express / Four Normal / Five Normal
CANDIDATE
NAME
CENTRE INDEX
S
NUMBER NUMBER
MATHEMATICS 4016/01
Paper 1 15 September 2009
2 hours
Candidates answer on the Question Paper.
READ THESE INSTRUCTIONS FIRST
Write your name, centre number and index number in the spaces at the top of this page
and on all the work you hand in.
Write in dark blue or black pen both sides of the paper.
You may use a pencil for any diagrams or graphs.
Do not use staples, paper clips, highlighters, glue or correction fluid.
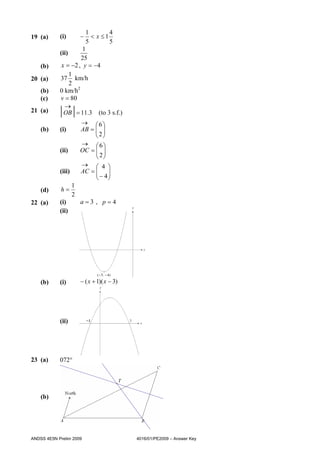
Answer all the questions.
If working is needed for any question it must be neatly and clearly shown in the space
below the question.
Omission of essential working will result in loss of marks.
Calculators should be used where appropriate.
If the degree of accuracy is not specified in the question, and if the answer is not exact,
give the answer to three significant figures. Give answers in degrees to one decimal
place.
For π, use either your calculator value or 3.142, unless the question requires the
answer in terms of π.
At the end of the examination, fasten all your work securely together.
The number of marks is given in brackets [ ] at the end of each question or part
question.
The total of the marks for this paper is 80.
For Examiner's Use
80
This document consists of 20 printed pages.
ANDSS 4E5N Prelim 2009 4016/01 [Turn over

2. 2
Mathematical Formulae
Compound Interest
n
⎛ r ⎞
Total amount = P⎜1 + ⎟
⎝ 100 ⎠
Mensuration
Curved surface area of a cone = πrl
Surface area of a sphere = 4πr 2
1 2
Volume of a cone = πr h
3
4 3
Volume of a sphere = πr
3
1
Area of triangle ABC = ab sin C
2
Arc length = rθ , where θ is in radians
1 2
Sector area = r θ , where θ is in radians
2
Trigonometry
a b c
= =
sin A sin B sin C
a 2 = b 2 + c 2 − 2bc cos A
Statistics
Σfx
Mean =
Σf
2
Σfx 2 ⎛ Σfx ⎞
Standard deviation = −⎜
⎜ Σf ⎟⎟
Σf ⎝ ⎠
ANDSS 4E5N Prelim 2009 4016/01/PE2009 [Turn over

3. 3
For
Examiner's 1 Given that x = 4.8 × 10 −9 and y = 2.5 × 1013 , calculate the following, giving your For
Examiner's
Use answers in standard form. Use
(a) 3x
(b) xy −1
Answer (a) ____________________ [1]
(b) ____________________ [1]
2 A group of 35 Andersonians sat for a math test.
The results are displayed in the dot diagram below.
•
•
• • •
• • • •
• • • • • •
• • • • • • • • •
• • • • • • • • • • •
60 70 80 90 100
(a) For the distribution above, write down
(i) the modal mark,
(ii) the median mark.
(b) The same data is to be represented on a pie chart.
Calculate the angle of the sector representing Andersonians who score 70 marks
or less in the test.
Answer (a) (i) _____________ marks [1]
(ii) _____________ marks [1]
(b) ____________________ ° [1]
ANDSS 4E5N Prelim 2009 4016/01/PE2009 [Turn over

4. 4
For −2 For
⎛ 2 p +1 2 ⎞
Simplify ⎜ ⎟
Examiner's Examiner's
Use 3 (a) ⎜ 2p ⎟ . Use
⎝ ⎠
x
⎛1⎞
(b) Given that ⎜ ⎟ × 2 = 1 , find the value of x.
⎝4⎠
Answer (a) ____________________ [2]
(b) x = _________________ [1]
4 A tank is filled with water.
At 10 40, water started to leak out from a small crack at the bottom of the tank.
The water level was then 3.7 cm above a mark on the wall of the tank.
At 12 20, the water level was 0.7 cm below the mark.
Assuming that the water leaked out at a constant rate, find
(a) the rate of water leakage, giving your answer in centimeters per hour,
(b) the height of the water level relative to the mark at noon.
Answer (a) ____________________ cm/h [1]
(b) ________________________ [2]
For
5 The temperature in City A and City B are x°C and −y°C respectively. For
ANDSS 4E5N Prelim 2009 4016/01/PE2009 [Turn over

5. 5
Examiner's Write down an expression for the mean of the two temperatures. Examiner's
Use Use
Answer ____________________ °C [1]
6 Three identical sectors are cut from the corners of
an equilateral triangle, leaving the remaining shape
as shown as the shaded region.
If the length of the arc of each sector is 7π cm,
find the area of the remaining shape.
Give your answer correct to 3 significant figures.
Answer ____________________ cm2 [3]
For 7 (a) Express in standard form, 0.00045 kg in mg. For
Examiner's Examiner's
Use Use
ANDSS 4E5N Prelim 2009 4016/01/PE2009 [Turn over

6. 6
(b) Express
(i) 9.988 to 2 significant figures,
(ii) 3.012 to 1 decimal place.
Answer (a) ____________________ mg [1]
(b) (i) ____________________ [1]
(ii) ____________________ [1]
8 The coordinates of the points A and B are (0, 5) and (0, −7) respectively.
3
Line AD cuts the x-axis at C and has gradient − .
4
Line BD has equation y = −7 .
(a) Write down the equation of line AD.
(b) Find the coordinates of D.
(c) Find the length of AD.
AC
(d) Find the value of .
CD
Answer (a) ____________________ [1]
(b) ( ________ , ________ ) [1]
(c) _______________ units [1]
(d) ____________________ [1]
ANDSS 4E5N Prelim 2009 4016/01/PE2009 [Turn over

7. 7
For
Examiner's
9 In the diagram, AB = 5 cm , For
Examiner's
2
AC = 11 cm and sin ∠ACB =
Use Use
.
5
(a) Write down the value of sin ∠ACD .
(b) Without finding any angle,
calculate the value of sin ∠ABC .
Answer (a) ____________________ [1]
(b) ____________________ [2]
2
10 Given that y = , where x > k .
x−π
(a) State the value of k.
(b) Rearrange the formula to express x in terms of y and π.
Answer (a) k = ____________________ [1]
(b) x = ____________________ [2]
ANDSS 4E5N Prelim 2009 4016/01/PE2009 [Turn over

8. 8
For 11 The table below shows the number of canned drinks purchased from two vending For
Examiner's Examiner's
Use machines, X and Y on a certain day. Use
Each vending machine sells three types of canned drinks; barley, cola and soda.
Barley Cola Soda
Machine X 18 31 25
Machine Y 26 x 19
The cost of a can of barley, a can of cola and a can of soda are 70 cents, 90 cents and
y cents respectively.
The information can be represented by matrices P and Q where
⎛ 70 ⎞
⎛ 18 31 25 ⎞ ⎜ ⎟
P=⎜ ⎜ 26 x 19 ⎟ ⎟ and Q = ⎜ 90 ⎟ .
⎝ ⎠ ⎜ y⎟
⎝ ⎠
⎛ 6300 ⎞
Given that PQ = ⎜
⎜ 5330 ⎟ .
⎟
⎝ ⎠
(a) Explain what PQ represents.
(b) Find the values of x and y.
Answer (a) ____________________________________________________________ [1]
____________________________________________________________ [1]
(b) x = ____________________ [2]
y = ____________________ [2]
For
12 (a) P, Q and R are subsets of the Universal set ε where P ⊂ Q , P ∩ R ≠ ∅ and For
ANDSS 4E5N Prelim 2009 4016/01/PE2009 [Turn over

9. 9
Examiner's
Use
Q′ ∩ R ≠ ∅ . Examiner's
Use
Add the sets Q and R on the Venn diagram shown in the answer space.
Answer (a)
[2]
(b) ε = { x : x is an integer and 10 < x ≤ 20 }
A = { x : x is a prime number }
B = { x : x is an integer ending in 3 }
C = { x : x + 1 is divisible by 3 }
(i) List the elements of A′.
(ii) Find the value of n( B ∪ C ) .
(iii) Describe, in words, as simply as possible, the element(s) contained in
A∩ B .
Answer (b) (i) A′ = ____________________ [1]
(ii) n( B ∪ C ) = ______________ [1]
(iii) ____________________________________________________________ [1]
For 13 (a) For the data below, state whether the mean or the median is a better measure of For
Examiner's Examiner's
ANDSS 4E5N Prelim 2009 4016/01/PE2009 [Turn over

10. 10
Use average, justifying your answer. Use
x 0 1 2 3 180
Frequency 15 18 16 14 1
(b) The lifespans, in hours, of batteries of two brands A and B are given below.
The lifespans of both brands of batteries are guaranteed by the manufacturer
to be at least 35 hours.
Brand A
Lifespan (x h) 35 ≤ x < 40 40 ≤ x < 45 45 ≤ x < 50 50 ≤ x < 55
Frequency 3 20 42 15
Brand B
Mean = p hours
Standard deviation = q hours
(i) Calculate the mean lifespan (in hours) and standard deviation for
Brand A batteries.
(ii) The average lifespan of Brand B batteries are shorter and less consistent
than those of Brand A. Write down the range of values of p and q which
will satisfy the above conditions.
Answer (a) The __________ is a better measure because ____________________ [1]
________________________________________________________ [1]
(b) (i) Mean = _____________ h [2]
Standard deviation = _____________ h [2]
(ii) The range of values of p is ____________________ [2]
The range of values of q is ____________________ [2]
ANDSS 4E5N Prelim 2009 4016/01/PE2009 [Turn over

11. 11
For 3 For
Examiner's 14 (a) Given that 1 − S is proportional to T and T = 2 when S = . Examiner's
Use 4 Use
Find a formula connecting S and T.
1
(b) Given that y is inversely proportional to x n and y is of its original value
4
when x is doubled. Calculate the value of n.
Answer (a) ____________________ [2]
(b) n = _________________ [2]
ANDSS 4E5N Prelim 2009 4016/01/PE2009 [Turn over

12. 12
For
Examiner's 15 (a) Expand and simplify ( x + y ) 2 − x(2 y − x) For
Examiner's
Use Use
(b) Factorise completely
(i) 8 p 2 − 16 pq + 8q 2
(ii) m 2 − 9(n − m) 2
Answer (a) ______________________ [1]
(b) (i) ____________________ [1]
(ii) ____________________ [2]
16 Each of the exterior angles of a polygon is 26°, except for one which is 74°.
Find the number of sides of this polygon.
Answer ____________________ [2]
For 17 (a) Express 600 as the product of its prime factor, leaving your answer in For
ANDSS 4E5N Prelim 2009 4016/01/PE2009 [Turn over

13. 13
Examiner's index notation. Examiner's
Use Use
(b) Given that A = 23 × 32 × 5 × 7 , find
(i) the highest common factor of 600 and A,
(ii) the smallest positive integer p such that 600 × A× p is a perfect square.
Answer (a) ____________________ [1]
(b) (i) _________________ [1]
(ii) _________________ [1]
18 Adam bought two model cars which are geometrically similar.
The ratio of the heights of the cars is 3 : 4.
(a) The length of the larger car is 36 cm. Find the length of the smaller car.
(b) The mass of the smaller car is 3.6 kg. Find the mass of the bigger car.
Answer (a) ____________________ cm [1]
(b) ____________________ kg [1]
For
Examiner's
19 (a) (i) Solve − 3 < 5 x − 2 ≤ 7 For
Examiner's
ANDSS 4E5N Prelim 2009 4016/01/PE2009 [Turn over

14. 14
Use Use
(ii) Hence write down the least possible value of ( x − 2) 2 .
(b) Solve the simultaneous equations.
3x − 2 y = 2
4( x + 1) = y
Answer (a) (i) ____________________ [1]
(ii) ____________________ [1]
(b) x = ____________________ [3]
y = ____________________ [3]
For 20 The diagram shows the speed-time graph of a car traveling from Town P to Town Q. For
Examiner's Examiner's
ANDSS 4E5N Prelim 2009 4016/01/PE2009 [Turn over

15. 15
Use Speed (km/h) Use
v
50
Time (t hours)
0 4 6 9
(a) Calculate the speed when t = 3 .
(b) Find the acceleration when t = 6 .
(c) The acceleration when t = 8 is 10 km/h2.
Find the value of v.
Answer (a) __________________ km/h [1]
(b) __________________ km/h2 [1]
(c) v = ____________________ [2]
For 21 OABC is a rhombus and the position vectors of the points A and B are given by For
Examiner's Examiner's
Use Use
ANDSS 4E5N Prelim 2009 4016/01/PE2009 [Turn over

16. 16
→ ⎛ 2⎞ → ⎛8⎞
OA = ⎜ ⎟ and OB = ⎜ ⎟ .
⎜ 6⎟ ⎜8⎟
⎝ ⎠ ⎝ ⎠
→
(a) Find OB .| |
(b) Express as a column vector
→
(i) AB
→
(ii) OC
→
(iii) AC
→ → → ⎛ 4h + 6 ⎞
(c) Given that CD = h AC , show that OD = ⎜
⎜ 2 − 4h ⎟ .
⎟
⎝ ⎠
(d) If the point D lies on the x-axis, find the value of h.
Answer (a) ____________________________ [1]
(b) (i) _________________________ [1]
(ii) _________________________ [1]
(iii) _________________________ [1]
(c) Working shown in the space above. [2]
(d) ____________________________ [1]
For
Examiner's 22 (a) The graph of y = 2( x + a ) 2 − p has a turning point at A (−3, −4). For
Examiner's
ANDSS 4E5N Prelim 2009 4016/01/PE2009 [Turn over

17. 17
Use Use
(i) State the value of a and of p.
(ii) Sketch the graph of y = 2( x + a ) 2 − p .
(b) (i) Factorise − x 2 + 2 x + 3 .
(ii) Sketch the graph of y = − x 2 + 2 x + 3 .
Answer (a) (i) a = __________ , p = __________ [2]
(ii)
[1]
(b) (i) ____________________________ [1]
(ii)
[1]
ANDSS 4E5N Prelim 2009 4016/01/PE2009 [Turn over

18. 18
For 23 The diagram shows triangle ABC on a horizontal plane. For
Examiner's Examiner's
Use Use
(a) Find the bearing of B from A.
Answer (a) ____________________ [1]
(b) The point T is equidistant from the points B and C and is also equidistant from
the lines AB and BC.
On the diagram, mark and label the point T.
Answer (b) [2]
ANDSS 4E5N Prelim 2009 4016/01/PE2009 [End of paper

19. ANDERSON SECONDARY SCHOOL
Secondary Four Express / Five Normal / Four Normal
Preliminary Examination 2009
MATHEMATICS Paper 1 4016/01
1 (a) 1.2 × 10 −4 12 (a)
(b) 1.92 × 10 −22
2 (a) (i) 100
(ii) 90
(b) 72° (b) (i) A′ = { 12, 14, 15, 16, 18, 20 }
1
3 (a) (ii) n( B ∪ C ) = 5
8
1 (iii) The set of prime numbers that
(b) x=
2 end in 3.
4 (a) 2.64 cm/h 13 (a) The median is a better measure
(b) 0.18 cm above the mark because there is an extreme value 180
x− y in the set of data which will distort
5 °C
2 the mean.
6 71.1 cm2 (b) (i) Mean = 46.8 h
7 (a) 4.5 × 10 2 mg Standard deviation = 3.77 h
(b) (i) 10 (ii) 35 ≤ p < 46.8 , q > 3.77
1
(ii) 3.0 14 (a) 1− S = T
4
3
8 (a) y = − x+5 (b) n=2
4
(b) (16, −7) 15 (a) 2x 2 + y 2
(c) 20 units (b) (i) 8( p − q ) 2
5
(d) (ii) (3n − 2m)( 4m − 3n)
7
2
9 (a) 16 12 sides
5
22
(b) 17 (a) 600 = 2 3 × 3 × 5 2
25
10 (a) k=π (b) (i) 120
4
(b) x= 2 +π (ii) 105
y
11 (a) The total amount (in cents) collected 18 (a) 27 cm
from the sales of the three types of 8
(b) 8 kg
drinks in each machine on a certain 15
day.
(b) x = 20 , y = 90
ANDSS 4E5N Prelim 2009 4016/01/PE2009 – Answer Key

20. 1 4
19 (a) (i) −< x ≤1
5 5
1
(ii)
25
(b) x = −2 , y = −4
1
20 (a) 37 km/h
2
(b) 0 km/h2
(c) v = 80
→
21 (a) | |
OB = 11.3 (to 3 s.f.)
→ ⎛6⎞
(b) (i) AB = ⎜ ⎟
⎜ 2⎟
⎝ ⎠
→ ⎛6⎞
(ii) OC = ⎜ ⎟
⎜ 2⎟
⎝ ⎠
→ ⎛ 4 ⎞
(iii) AC = ⎜ ⎟
⎜ − 4⎟
⎝ ⎠
1
(d) h=
2
22 (a) (i) a=3 , p =4
(ii)
(b) (i) − ( x + 1)( x − 3)
(ii)
23 (a) 072°
T
(b)
ANDSS 4E5N Prelim 2009 4016/01/PE2009 – Answer Key