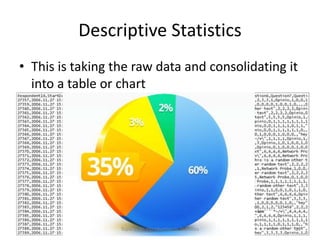
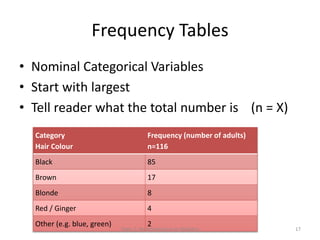
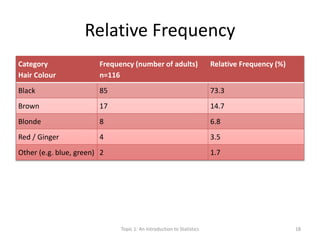
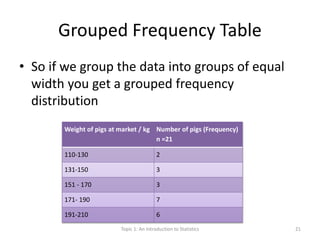
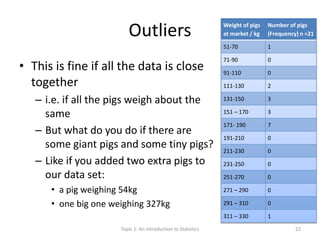
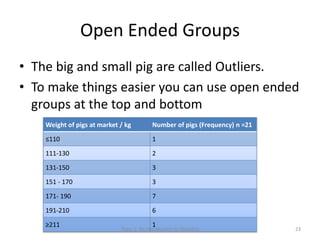
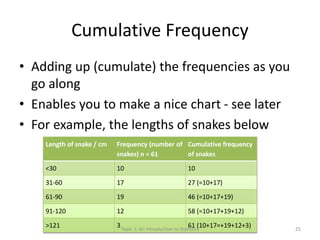
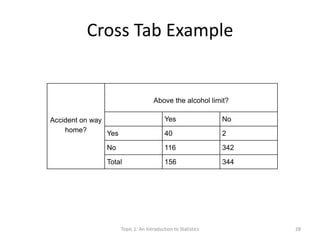
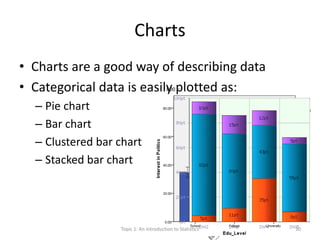
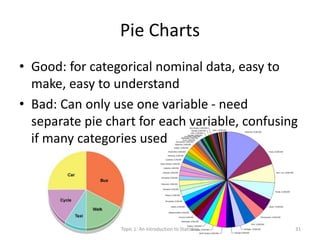
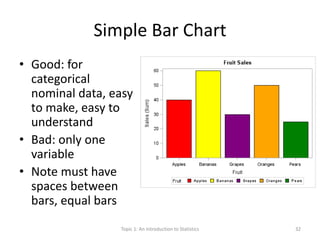
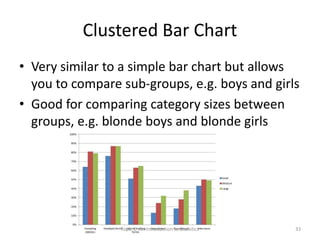
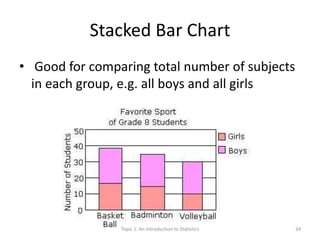
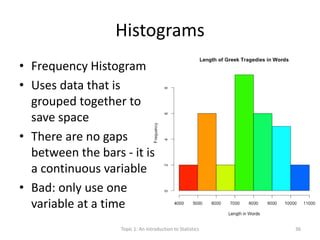
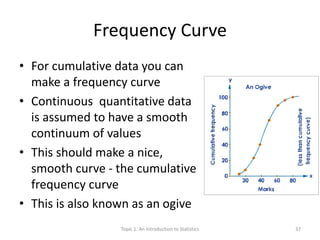
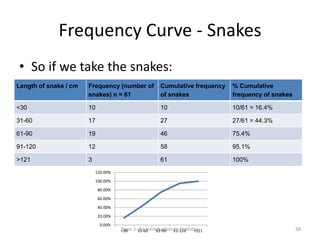
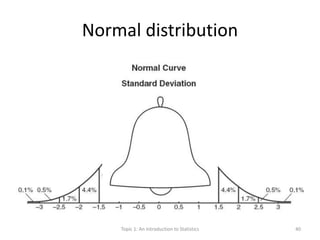
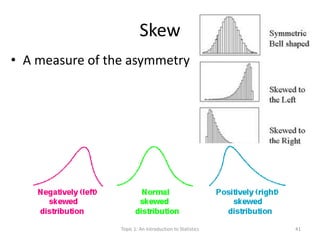
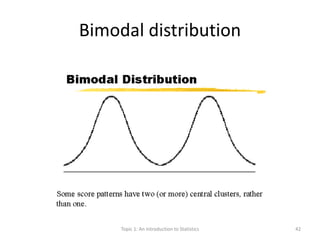
This document provides an introduction to statistics. It defines key statistical concepts like variables, data, and different types of variables. Descriptive statistics are used to summarize raw data through tables and charts. Different types of charts are described that are suitable for categorical or quantitative variables. The goals are to classify variables, choose appropriate charts and tables, and understand how to describe and communicate data.