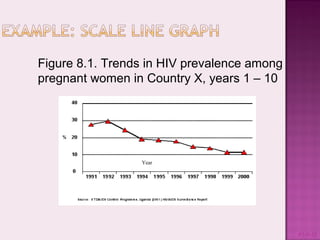
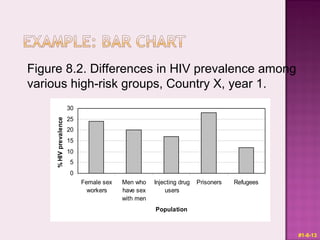
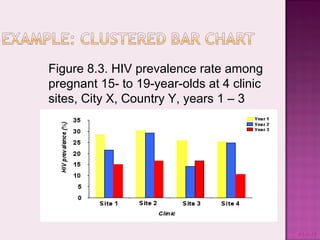
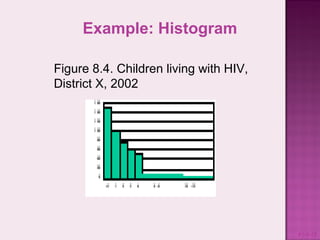
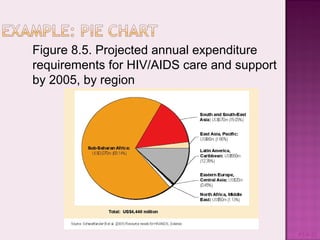
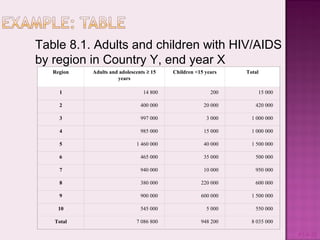
This document discusses presenting and discussing data in charts, graphs, and tables. It outlines the types of charts and graphs that are appropriate for different types of surveillance data, including line graphs to show trends over time, bar charts to compare categories, histograms to show distributions, pie charts to compare parts of a whole, and tables. The purpose is to facilitate analysis, interpretation, and communication of complex data through clear visual representations. Key considerations include using simple, labeled, and narrative formats that avoid scaling issues when comparing variables.

1. Presenting and Discussing
Data in Charts, Graphs and
Tables

2.  By the end of this unit you should be able
to:
 list the variables for analysing surveillance data
 identify the types of charts and graphs and when
the use of each is appropriate
#1-8-3

3.  Person: Who develops a disease (for example, by
age group or sex)? Are the distributions changing
over time?
 Place: Where are cases occurring? Is the
geographical distribution changing over time?
 Time: Is the number of reported cases changing
over time?
#1-8-4

4.  The purpose of developing clearly
understandable tables, charts and graphs
is to facilitate:
 analysis of data
 interpretation of data
 effective, rapid communication on complex
issues and situations
#1-8-5

5.  Categorical variables refer to items that
can be grouped into categories.
Ordinal variables are those that have a natural
order.
Nominal variables represent discrete
categories without a natural order.
 Dichotomous variables have only two categories
 Continuous variables are items that occur
in numerical order.
#1-8-6

6.  Simpler is better.
 Graphs, tables and charts can be used together.
 Use clear descriptive titles and labels.
 Provide a narrative description of the highlights.
 Don’t compare variables with different scales of
magnitude. #1-8-7

7.  A diagram shown as a series of one or more
points, lines, line segments, curves or areas
 Represents variation of a variable in comparison
with that of one or more other variables
#1-8-8

8.  Scale line graph: represents frequency
distributions over time
 Y-axis represents frequency.
 X-axis represents time.
#1-8-9

9. #1-8-10
Year
Figure 8.1. Trends in HIV prevalence among
pregnant women in Country X, years 1 – 10

10.  Y-axis should be shorter than X-axis
 Start the Y-axis with zero
 Determine the range of values needed
 Select an interval size
#1-8-11

11.  Uses differently coloured or patterned bars
to represent different classes
 Y-axis represents frequency
 X-axis may represent time or different
classes
#1-8-12

12. 0
5
10
15
20
25
30
Female sex
workers
Men who
have sex
with men
Injecting drug
users
Prisoners Refugees
Population
%HIVprevalence
Figure 8.2. Differences in HIV prevalence among
various high-risk groups, Country X, year 1.
#1-8-13

13.  Arrange categories that define bars in a natural order
(for example, age).
 If natural order does not exist, define categories by
name, such as country, sex or marital status.
 Position the bars either vertically or horizontally.
 Make bars the same width.
 Length of bars should be proportional to the frequency
of event.
#1-8-14

14.  Bars can be presented as clusters of sub-
groups in clustered bar charts.
 These are useful to compare values across
categories.
 They are sometimes called stacked bar
charts.
#1-8-15

15. Figure 8.3. HIV prevalence rate among
pregnant 15- to 19-year-olds at 4 clinic
sites, City X, Country Y, years 1 – 3
#1-8-16

16.  Show no more than three sub-bars within a
group of bars.
 Leave a space between adjacent groups of bars.
 Use different colours or patterns to show
different sub-groups for the variables being
shown.
 Include a legend that interprets the different
colours and patterns.
#1-8-17

17.  A representation of a frequency distribution
by means of rectangles
 Width of bars represents class intervals and
height represents corresponding frequency
#1-8-18

18. Example: Histogram
#1-8-19
Figure 8.4. Children living with HIV,
District X, 2002

19.  A circular (360 degree) graphic
representation
 Compares subclasses or categories to the
whole class or category using differently
coloured or patterned segments
#1-8-20

20. #1-8-21
Figure 8.5. Projected annual expenditure
requirements for HIV/AIDS care and support
by 2005, by region

21.  A graph used to plot variables by
geographic locations
#1-8-22

22. Figure 8.6. HIV Prevalence in Adults
in Africa, end 2003
#1-8-23
Source: UNAIDS, 2003

23.  A rectangular arrangement of data in
which the data are positioned in rows and
columns.
 Each row and column should be labelled.
 Rows and columns with totals should be
shown in the last row or in the right-hand
column.
#1-8-24

24. #1-8-25
Table 8.1. Adults and children with HIV/AIDS
by region in Country Y, end year X
Region Adults and adolescents 15≥
years
Children <15 years Total
1 14 800 200 15 000
2 400 000 20 000 420 000
3 997 000 3 000 1 000 000
4 985 000 15 000 1 000 000
5 1 460 000 40 000 1 500 000
6 465 000 35 000 500 000
7 940 000 10 000 950 000
8 380 000 220 000 600 000
9 900 000 600 000 1 500 000
10 545 000 5 000 550 000
Total 7 086 800 948 200 8 035 000

25.  Surveillance data can be analysed by
person, place or time.
 Depending on your data, you can choose
from a variety of chart and graph formats,
including pie charts, histograms, tables,
etc.
 Using several simpler graphics is more
effective than attempting to combine all
of the information into one figure.
#1-8-26