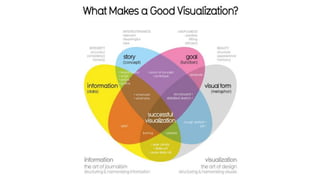
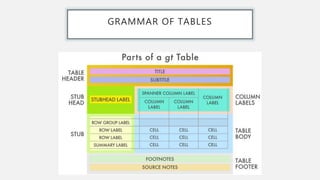
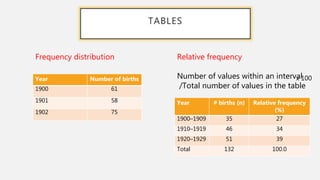
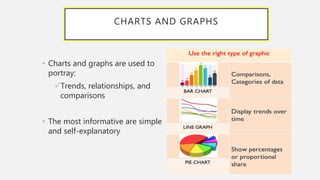
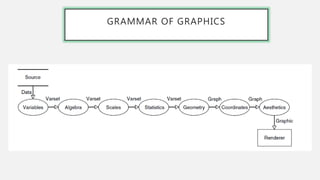
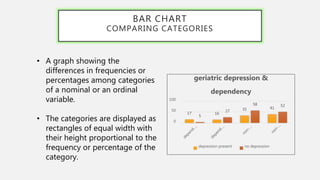
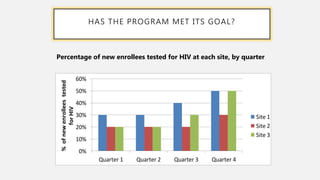
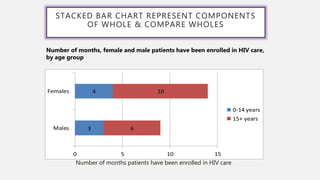
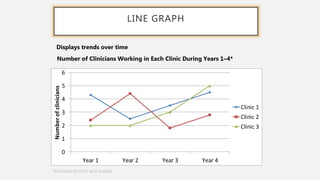
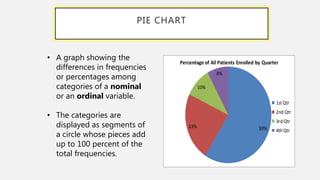
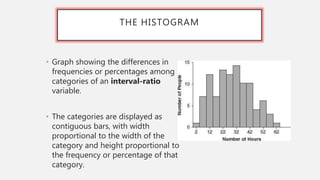
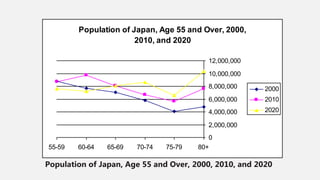
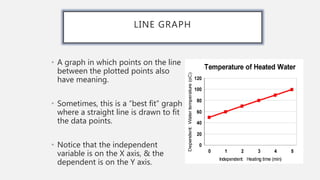
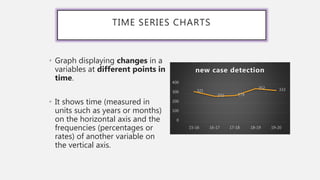
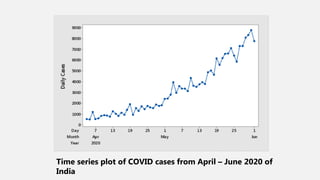
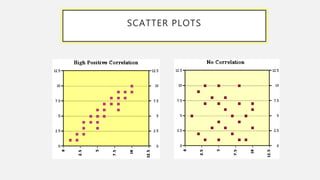
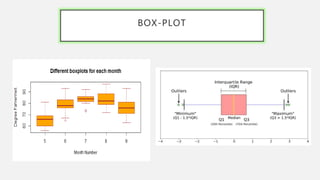
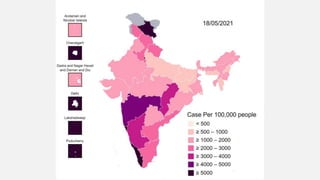
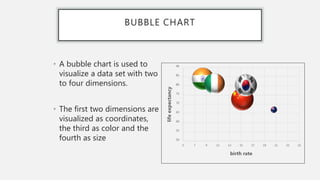
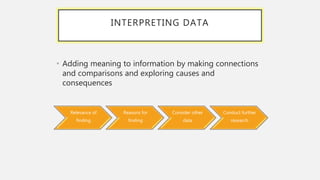
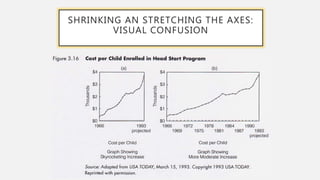
This document provides an overview of data visualization. It discusses the importance of data visualization and provides guidance on summarizing data using tables and charts/graphs. Key types of charts are described, including bar charts, line graphs, pie charts, histograms, and more. It also covers interpreting data and potential distortions that can occur in graphs. The document emphasizes labeling components, choosing the right graph for the data, and using visualization to detect patterns and make comparisons.

1. DATA VISUALIZATION
Presenter - Dr. Naveen Shyam
Department of community medicine,
SNPH,MGIMS ,sevagram

2. WHAT IS DV?
WHY DV IS
IMPORTANT?

4. SUMMARIZING DATA- BASIC GUIDANCE
• Tables
• Simplest way to summarize
data
• Charts and graphs
• Visual representation of
data
• Ensure graphic has a title
• Label the components of your
graphic
• Indicate source of data with
date
• Provide number of
observations (n=xx) as a
reference point
• Add footnote if more
information is needed
Data are presented as
absolute numbers or
percentages

5. GRAMMAR OF TABLES

6. TABLES
Year Number of births
1900 61
1901 58
1902 75
Frequency distribution
Year # births (n) Relative frequency
(%)
1900–1909 35 27
1910–1919 46 34
1920–1929 51 39
Total 132 100.0
Relative frequency
Number of values within an interval
/Total number of values in the table
x 100

7. CHARTS AND GRAPHS
• Charts and graphs are used to
portray:
Trends, relationships, and
comparisons
• The most informative are simple
and self-explanatory

8. GRAMMAR OF GRAPHICS
• Always start with the data, identify the dimensions you want to visualize.
DATA and
MAPPING • Confirm the axes based on the data dimensions, positions of various data
points in the plot. Also check if any form of encoding is needed including size,
shape, color and so on which are useful for plotting multiple data dimensions.
AESTHETICS
• Do we need to scale the potential values, use a specific scale to represent
multiple values or a range?
SCALE
• These are popularly known as ‘geoms’. This would cover the way we would
depict the data points on the visualization. Should it be points, bars, lines
and so on?
GEOMETRIC OBJECTS
• Do we need to show some statistical measures in the visualization like measures
of central tendency, spread, confidence intervals?
STATISTICS
• Do we need to create subplots based on specific data dimensions?
FACETS
• What kind of a coordinate system should the visualization be based on —
should it be cartesian or polar?
CO-ORDINATE SYSTEM

9. COMPONENTS OF THE LAYERED GRAMMAR
OF GRAPHICS

11. GRAMMAR OF GRAPHICS

12. BAR CHART
COMPARING CATEGORIES
• A graph showing the
differences in frequencies or
percentages among categories
of a nominal or an ordinal
variable.
• The categories are displayed as
rectangles of equal width with
their height proportional to the
frequency or percentage of the
category.
17 16
35 41
5
27
58 52
0
50
100
geriatric depression &
dependency
depression present no depression

13. HAS THE PROGRAM MET ITS GOAL?
0%
10%
20%
30%
40%
50%
60%
Quarter 1 Quarter 2 Quarter 3 Quarter 4
%
of
new
enrollees
tested
for
HIV
Site 1
Site 2
Site 3
Percentage of new enrollees tested for HIV at each site, by quarter

14. STACKED BAR CHART REPRESENT COMPONENTS
OF WHOLE & COMPARE WHOLES
3
4
6
10
0 5 10 15
Males
Females
0-14 years
15+ years
Number of months patients have been enrolled in HIV care
Number of months, female and male patients have been enrolled in HIV care,
by age group

15. LINE GRAPH
0
1
2
3
4
5
6
Year 1 Year 2 Year 3 Year 4
Number
of
clinicians
Clinic 1
Clinic 2
Clinic 3
Number of Clinicians Working in Each Clinic During Years 1–4*
*Includes doctors and nurses
Displays trends over time

16. PIE CHART
59%
23%
10%
8%
Percentage of All Patients Enrolled by Quarter
1stQtr
2nd Qtr
3rdQtr
4thQtr
• A graph showing the
differences in frequencies
or percentages among
categories of a nominal
or an ordinal variable.
• The categories are
displayed as segments of
a circle whose pieces add
up to 100 percent of the
total frequencies.

17. THE HISTOGRAM
• Graph showing the differences in
frequencies or percentages among
categories of an interval-ratio
variable.
• The categories are displayed as
contiguous bars, with width
proportional to the width of the
category and height proportional to
the frequency or percentage of that
category.

18. THE FREQUENCY POLYGON
• Graph showing the differences in frequencies or percentages
among categories of an interval-ratio variable.
• Points representing the frequencies of each category are
placed above the midpoint of the category and are jointed by a
straight line.

19. Population of Japan, Age 55 and Over, 2000, 2010, and 2020
Population of Japan, Age 55 and Over, 2000,
2010, and 2020
0
2,000,000
4,000,000
6,000,000
8,000,000
10,000,000
12,000,000
55-59 60-64 65-69 70-74 75-79 80+
2000
2010
2020

20. LINE GRAPH
• A graph in which points on the line
between the plotted points also
have meaning.
• Sometimes, this is a “best fit” graph
where a straight line is drawn to fit
the data points.
• Notice that the independent
variable is on the X axis, & the
dependent is on the Y axis.

21. TIME SERIES CHARTS
• Graph displaying changes in a
variables at different points in
time.
• It shows time (measured in
units such as years or months)
on the horizontal axis and the
frequencies (percentages or
rates) of another variable on
the vertical axis.
321
272 279
352 333
0
100
200
300
400
15-16 16-17 17-18 18-19 19-20
new case detection

22. Time series plot of COVID cases from April – June 2020 of
India

23. PICTOGRAPH
• Uses pictures and symbols to display
data.
• Each picture or symbol can represent
more than one object.
• A key tells what each picture
represents.

24. SCATTER PLOTS
A graph of data that is a set of points.

25. BOX-PLOT
Box Plot

26. THE STATISTICAL MAP
• We can display dramatic geographical changes in American
society by using a statistical map.
• Maps are especially useful for describing geographical
variations in variables, such as population distribution, voting
patterns, crimes rates, or labor force participation.

28. BUBBLE CHART
• A bubble chart is used to
visualize a data set with two
to four dimensions.
• The first two dimensions are
visualized as coordinates,
the third as color and the
fourth as size 50
55
60
65
70
75
80
85
90
5 7 9 11 13 15 17 19 21 23 25
life
expectancy
birth rate

29. INTERPRETING DATA
• Adding meaning to information by making connections
and comparisons and exploring causes and
consequences
Relevance of
finding
Reasons for
finding
Consider other
data
Conduct further
research

30. INTERPRETATION – RELEVANCE OF
FINDING
• Does the indicator meet the target?
• How far from the target is it?
• How does it compare (to other time periods, other
facilities)?
• Are there any extreme highs and lows in the data?

31. Relevance of
finding
Reasons for
finding
Consider other
data
Conduct further
research
INTERPRETATION – POSSIBLE CAUSES?
• Supplement with expert opinion
• Others with knowledge of the program or target
population

32. Relevance of
finding
Reasons for
finding
Consider other
data
Conduct further
research
INTERPRETATION – CONSIDER OTHER
DATA
• Use routine service data to clarify questions
• Use other data sources

33. INTERPRETATION – OTHER DATA
SOURCES
• Situation analyses
• Demographic and health surveys
• Performance improvement data
Relevance of
finding
Reasons for
finding
Consider other
data
Conduct further
research

34. INTERPRETATION – CONDUCT FURTHER
RESEARCH
• Data gap conduct further research
• Methodology depends on questions being asked and
resources available
Relevance of
finding
Reasons for
finding
Consider other
data
Conduct further
research

35. KEY MESSAGES
• Use the right graph for the right data
Tables – can display a large amount of data
Graphs/charts – visual, easier to detect patterns
• Label the components of your graphic
• Interpreting data adds meaning by making connections and
comparisons to program
• Service data are good at tracking progress & identifying concerns

36. DISTORTIONS IN GRAPHS
• Graphs not only quickly inform us; they can quickly deceive us.
• Because we are often more interested in general impressions than
in detailed analyses of the numbers, we are more vulnerable to
being swayed by distorted graphs.
What are graphical distortions?
How can we recognize them?

37. SHRINKING AN STRETCHING THE AXES:
VISUAL CONFUSION

38. WHY USE CHARTS AND GRAPHS?
• What do you lose?
×Ability to examine numeric
detail offered by a table
×Potentially the ability to see
additional relationships within
the data
×Potentially time: often we get
caught up in selecting colors
and formatting charts when a
simply formatted table is
sufficient
• What do you gain?
Ability to direct readers’
attention to one aspect of the
evidence
Ability to reach readers who
might otherwise be intimidated
by the same data in a tabular
format
Ability to focus on bigger picture
rather than perhaps minor
technical details

39. DATA VISUALIZATION TOOLS-
AN INTRODUCTION

40. THANK YOU