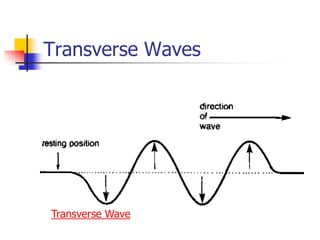
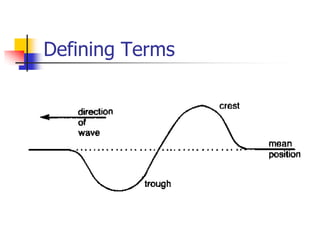
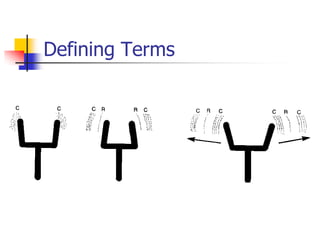
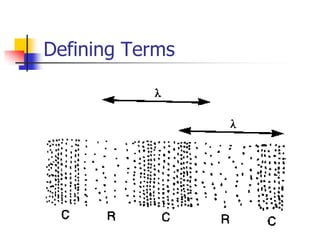
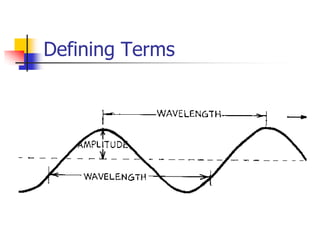
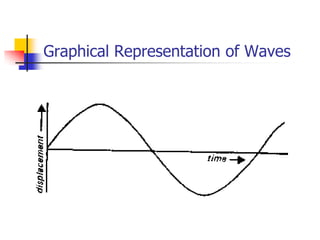
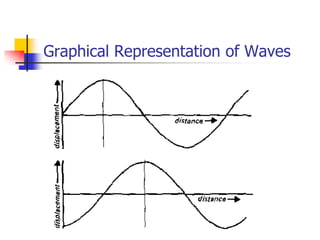
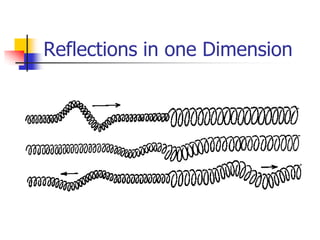
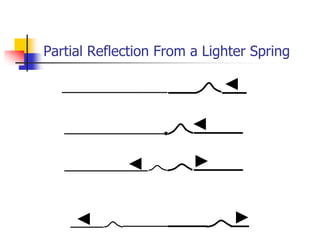
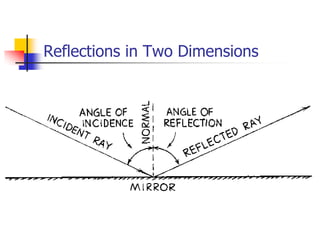
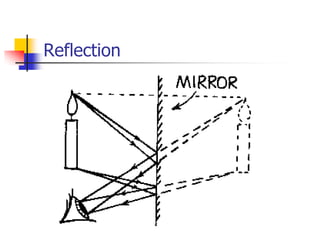
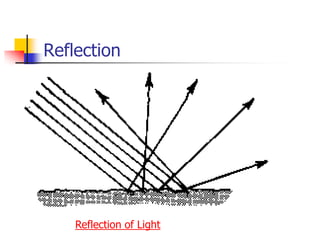
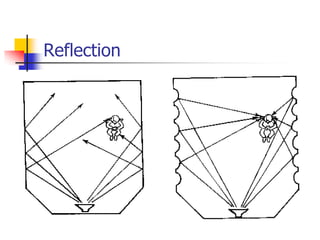
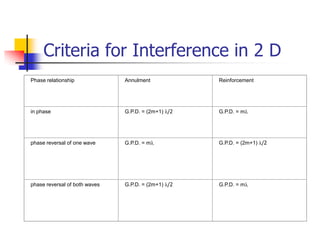
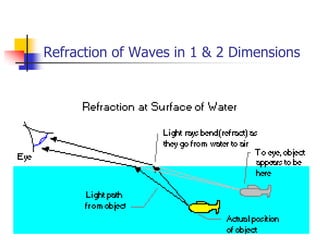
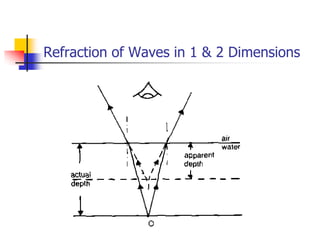
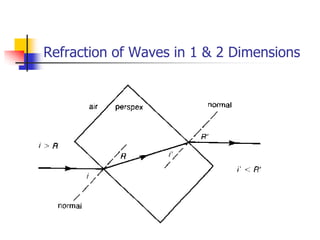
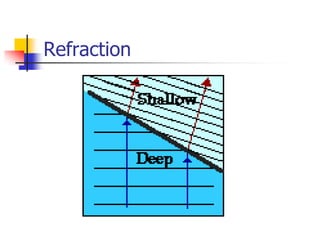
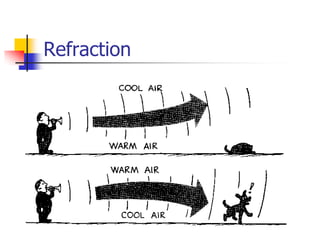
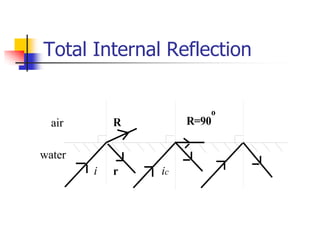
Waves transfer energy through a medium without transferring matter. There are two main types of waves: transverse waves, where the medium's particles move perpendicular to the wave's direction; and longitudinal waves, where particles move parallel. Characteristics like wavelength, frequency, amplitude, and speed define a wave's properties. Energy is transferred through reflections, where waves bounce back at the same angle they arrive. Reflections can be partial or total, depending on the boundary material.

1. Vibrations & Waves

2. WAVES
 Energy can be transferred in a number of
ways.
 A moving car is an example of energy in
motion
 Not only does the energy move the car
moves as well.
 Energy can move without the object/particle
moving with it.
 This occurs in waves.

3. Travelling Wave
Characteristics
 A surfer;
 sitting on their board,
 waiting for the right wave.
 While waiting;
 ocean waves pass under him,
 while he bobs up and down.
 Flick a slinky spring;
 wave passes along the slinky while,
 particles move up and down.

4. Travelling Wave
Characteristics
 Drop a stone in a still pond;
 you produce a wave that moves out
from the centre,
 in ever increasing circles.
 Check the water before and after the
wave passes,
 You find that the water,
 remained where it was.

5. Travelling Wave
Characteristics
 In these examples the particles vibrate
or oscillate.
 The wave has been transferred without
a transfer of matter.
 The signals from radio and T.V.’s are
waves.
 Sound and light travel as waves.

6. Transverse Waves
If you create a wave by shaking a slinky
up and down, the motion of the medium
is at right angles to the motion of the
wave.
 This type of wave is called
a transverse wave.

7. Transverse Waves
 Stretched strings in a musical
instrument
 ocean waves,
 radio and light
are all examples of transverse waves.

8. Transverse Waves
Transverse Wave

9. Longitudinal Waves
 When the particles of the medium move in
the same direction as the wave, it is known
as a longitudinal wave.
 They are less common.
 Sound travels as a longitudinal wave.

10. Longitudinal Waves
 In both forms, the energy can be
transferred as a single pulse, a number
of pulses, or a continuous wave.
 Particles may be set in motion by a
wave no particle travels far from its
initial position.

11. Longitudinal Waves
 As the wave particles set neighbouring
particles into motion the wave is
propagated through the
medium, energy is transferred in the
medium.

12. Longitudinal Waves
 Wavelength of a longitudinal wave
distance between successive
compressions or successive
rarefactions.

13. Defining Terms
 Medium:
 The substance through which the wave
moves the particles making up the
medium, are those which are displaced, as
the wave moves through it.

14. Defining Terms
 Displacement:
 The distance a particle has moved from its
mean position.

15. Defining Terms
 Crest:
 Positive displacement of a transverse
wave.
 Trough:
 Negative displacement of a transverse
wave.

16. Defining Terms

17. Defining Terms
 Compression:
 Regions of a longitudinal wave that;
 have a high density of particles.
 Rarefaction:
 Regions of a longitudinal wave that;
 have a low density of particles.

18. Defining Terms

19. Defining Terms

20. Defining Terms
 Wavelength:
 The distance covered in a complete wave
cycle.
 The distance between two consecutive
points in phase.
 Symbol Greek letter
 Unit (SI) metre.

21. Defining Terms

22. Defining Terms
 Amplitude:
 The difference between the maximum
displacement and the mean position.
 Symbol A
 Unit (SI) metre.

23. Defining Terms

24. Defining Terms
 Period:
 The time for one complete oscillation.
 Symbol T
 Unit (SI) second.

25. Defining Terms
 Frequency:
 Is the number of wavelengths generated
by a source in a second.
 Symbol f
 Unit (SI) Hertz (Hz)

26. Defining Terms
 Frequency and period are related by the
formula;
1
f
T

27. Defining Terms
 Wave Speed:
 Is the speed at which a given point on the
wave, is travelling through the medium.
 The product of frequency and wavelength.
Mathematically represented by
v =f
 Unit (SI) ms-1.

28. Defining Terms
 Characteristic of the
medium the wave
travels through.
 Sound waves in air
typically 330 ms-1 to 350 ms-1
depending on the density of the air
and four times faster in water.

29. Sound
Sound is a longitudinal wave, but it’s
speed depends on the medium
 Sound in a solid
 Sound in a gas
 Pulse of sound
 Sound in a bell jar
 Different atmosphere music playing

30. Speed of sound calculations
 What is the speed of sound for each of
these:
1. Travels 127m in 0.1 sec
2. Travels 1608 m in 4 sec
3. Travels 1493 cm in 0.01 sec
4. Travels 120km in 10 sec
Which answer is speed of sound in water,
air, diamond ?

31. Sound barrier

32. Sound barrier
 As an airplane approaches the speed of
sound, shock waves build up, creating
increase in drag, loss of lift, and loss of
control.
 When travelling near the speed of sound, the
plane came up against a "sound barrier"--as
though the velocity of sound represented a
wall through which a plane could not move.
 The sound barrier was broken in 1947.

33. Shock waves
 As an airplane flies
faster than the speed of
sound, it "pushes" on
the sound waves in front
of it. They continue to
travel at the same speed.
 The waves pile up
against each other as
they are created. These
are called shock waves.

34. Sonic Booms
 The shock waves will move out and back from the
plane, towards the ground. There is a sudden
change in pressure when the shock wave hits
your eardrum. You hear this as a loud sonic
boom.

35. Summary of Wave Speeds
WAVE TYPE MEDIUM SPEED (ms-1)
Sound Carbon Dioxide 260
Air 331
Hydrogen 1290
Pure Water 1410
Sea Water 1450
Glass 5500
Light Vacuum 2.997 x 108
Air 2.998 x 108
Glass (crown) 2.0 x 108
Earthquake Crust 3500 (transverse)
8000 (longitudinal)
Mantle 6500 (transverse)
11000 (longitudinal)

36. The Behaviour of Waves
 When a wave moves through a medium
the velocity and shape of that
wave, remains constant.
 This is so, no matter what the medium.

37. Graphical Representation of Waves

38. Graphical Representation of Waves

39. Reflections in one Dimension
 When a wave reaches a boundary
between two media some or all of the
wave bounces back, into the first
medium.

40. Reflections in one Dimension
 A pulse is sent along a slinky spring
which is attached at one end to a wall.
 All the energy is reflected back along
the spring, rather than into the wall.

41. Reflections in one Dimension
Reflection from a boundary

42. Reflection From a Fixed End

43. Reflections in one Dimension
 The pulse becomes inverted as it is
reflected.
 This is called phase reversal.
 This is why metals are so shiny.
 A Metal surface is rigid to the light
waves that shine upon it.

44. Reflections in one Dimension
 Most of the light is reflected apart from
a small energy loss, due to the friction
of, the vibrating electrons in the
surface.
 Metals can be used as mirrors for this
reason.

45. Reflection From a Free End

46. Reflections in one Dimension
 The part of the spring adjacent to the
boundary is free to be displaced, and
no phase change occurs on reflection.

47. Reflections in one Dimension
 If the wall is replaced with a heavy
spring as a new medium, some energy
is transmitted, some energy is reflected.
Reflection from a boundary

48. Reflections in one Dimension

49. Partial Reflection from a Heavier Spring
lighter spring
. heavier spring
.
.
.

50. Reflections in one Dimension
 The heavy spring acts as an imperfect
‘rigid’ boundary, partially reflecting the
pulse, with a change of phase but, also
partially transmitting it.

51. Reflections in one Dimension
 Two pulses of reduced amplitude move
at speeds characteristic of the media
 result.

52. Partial Reflection From a Lighter Spring
.

53. Reflections in one Dimension
 The lighter spring acts as an imperfect
‘free end’, partially reflecting the pulse,
without change of phase and, partially
transmitting it.
 Two pulses with reduced amplitude are
produced.

54. Reflections in Two Dimensions
 In one dimension the reflected wave
simply travels back, in the direction
from which it came.
 In two dimensions, the situation is a
little different.

55. Reflections in Two Dimensions
 Direction of incident & reflected waves
described by straight lines called rays.
 The incoming ray (incident ray) and the
reflected ray makes, equal angles with
the normal.

56. Reflections in Two Dimensions
 Angle between incident ray & normal
called the angle of incidence
 Angle between the reflected ray &
normal called the angle of reflection.

57. Reflections in Two Dimensions

58. Reflections in Two Dimensions
 Relationship is called Law of reflection.
 Law applies equally to both partially
reflected and, totally reflected waves.
 Stated mathematically:
 i= r
Reflection of light

59. Reflection
 If a lit candle is placed in front of a
plane mirror, rays of light are reflected
in all directions.
 There are an infinite number all obey
the law of reflection.

60. Reflection
 The rays diverge from the tip of the
flame and continue to diverge upon
reflection.
 These rays appear to originate from a
point located behind the mirror.

61. Reflection
 This is called a virtual image the light
does not actually pass through the
image, but behaves as though it
virtually did.
 The image appears as far behind the
mirror as the object is in front of it
and, the object and the image is the
same.

62. Reflection

63. Reflection

64. Reflection
 When the mirror is curved sizes &
distances of the object and image, are
no longer equal, but the law of
reflection still holds.

65. Reflection

66. Reflection

67. Reflection
Concave Mirror

68. Reflection
 For a rough surface each individual ray
obeys the law of reflection many
different angles light rays encounter in
striking a rough surface
cause, reflection in many directions.
 This is called diffuse reflection.

69. Reflection
Reflection of Light

70. Reflection

71. Diffraction
Diffraction is the
spreading out of a wave
as it passes through a
gap.
ƛ = d waves spread out
ƛ < d no change to wave

72. Criteria for Interference in 2 D
 Consider a ripple tank with two dippers
producing waves, of the same
frequency and in phase.
 A two dimensional standing wave would
be seen.

73. Criteria for Interference in 2 D

74. Criteria for Interference in 2 D
 Even if the dippers were out of phase
by radians ( /2), the 2D standing
wave pattern would still be seen.
 In both cases, the dippers maintain a
constant phase relationship, referred to
as mutually coherent sources.

75. Criteria for Interference in 2 D
 Mutually coherent wave sources
maintain a constant phase relationship.

76. Criteria for Interference in 2 D

77. Criteria for Interference in 2 D
 For a point to be on a nodal line
difference between its distance, from
one source and the other source, called
the geometric path difference, G.P.D.
must be an odd number of half
wavelengths.
 In the diagram above

78. Criteria for Interference in 2 D
 For any point on an antinodal line
G.P.D. must be an even number of /2.
 This means that reinforcement occurs
when G.P.D. = m ,
 m = 0,1,2,........

79. Criteria for Interference in 2 D
Phase relationship Annulment Reinforcement
in phase G.P.D. = (2m+1) /2 G.P.D. = m
phase reversal of one wave G.P.D. = m G.P.D. = (2m+1) /2
phase reversal of both waves G.P.D. = (2m+1) /2 G.P.D. = m

80. Refraction of Waves in 1 & 2 Dimensions
 Place a pencil in a glass of water it
appears bent, at the air/water interface.
 Bending or change in direction that
occurs at the boundary, of two different
media is called refraction.

81. Refraction of Waves in 1 & 2 Dimensions
 Place coin on bottom of empty coffee mug.
 Position yourself so the coin is just out of
view the coin becomes visible as water is added.
 The coin still appears to be on the bottom the
image of the coin and the bottom of the mug, must
have moved up.

82. Refraction of Waves in 1 & 2 Dimensions

83. Refraction of Waves in 1 & 2 Dimensions

84. Refraction of Waves in 1 & 2 Dimensions
 Water in a pond appears to be only ¾
its true depth.
 The depth an object appears to be is
called the apparent depth while its true
depth is called, the real depth.

85. Refraction of Waves in 1 & 2 Dimensions

86. Refraction of Waves in 1 & 2 Dimensions
 i = angle of incidence
 R = angle of refraction
 D = angle of deviation

87. Refraction of Waves in 1 & 2 Dimensions
 Angle of refraction is less than angle of
incidence when the 2nd medium is more
optically dense than the first medium,
such as when light travels from air to
glass.
 This is reversed when light travels from
glass to air.

88. Refraction of Waves in 1 & 2 Dimensions

89. Refraction of Waves in 1 & 2 Dimensions
 Light bends towards the normal when it enters
a more optically dense medium.
 Light bends away from the normal when it
enters a less optically dense medium.
 The amount the incident ray is deviated
depends on the nature of the transparent material

90. Refraction

91. Refraction

92. Refraction
 As the waves move more slowly in
shallow water the crests are closer
together.
 Diagram above each line represents a
crest, called a wavefront.

93. Refraction
 Waves can also be refracted in air.
 This can happen when winds are
uneven or, when sound travels through
air, of uneven temperature.

94. Refraction

95. Refraction

96. Total Internal Reflection
 Beam of light travelling through water
hits a water/air interface.
 Some light is refracted some reflected.

97. Total Internal Reflection
 As i increases the amount of reflected
light increases.
 At the critical angle, (ic) the light is
moving at right angles, to the normal.

98. Total Internal Reflection
 At angles greater than ic no light is
refracted, it is totally internally
reflected.

99. Total Internal Reflection
o
air R R=90
water
i r ic

100. Applications
 Optical fibre cable is a strand of glass
with a protective coating.
 The angle of incidence of the light is
greater than the critical angle, so all
light is reflected.

101. Applications
 This allows the light to be channelled
around corners, used by anyone from
mechanics, to doctors and dentists.

102. Applications
 Communications can also take advantage of
this phenomenon.
 Copper cables carry information as electrical
voltages, while optical cables can carry many
messages, as modulations of laser light in binary
signals,(‘on’ or ‘off’) at more than 40 million pulses a
second.