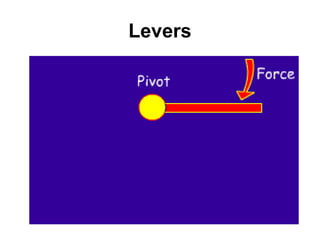
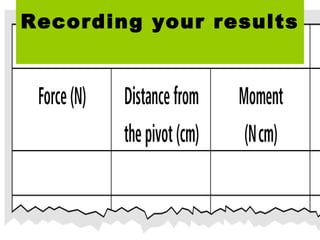
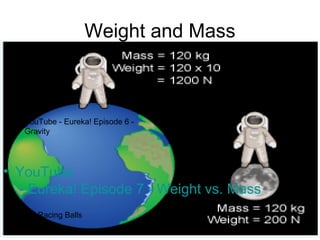
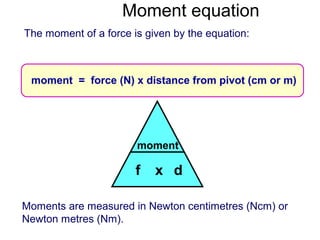
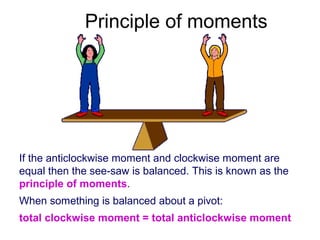
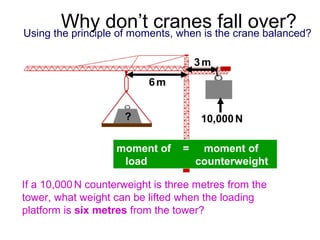
This document discusses levers and moments. It provides examples of levers in the body, such as bones and joints. It explains that the longer the lever, the bigger the force needed to move an object. It also discusses moments and how they are calculated by multiplying force by distance from the pivot. Examples are provided about balancing moments on a seesaw. The document also discusses how counterweights on cranes allow them to lift heavy loads by balancing the moments of the load and counterweight.

1. Balanced Forces

2. Levers

3. Write out the
statements that are
true.
• a The longer the lever, the bigger the
force that is needed to move an object.
• b It is easier to close a door if you push
the door close to the hinge
• c The shorter the lever, the bigger the
force that is needed to move an object
• d Joints are examples of pivots.
• e Bones are examples of levers.

4. C, D and E

5. Learning Objective
To investigate, through
practical experimentation,
the principle of moments.

7. • What do we need to record?
• How many columns will we need in
our table?
Recording your results

9. Recording your results

10. Weight and Mass
• YouTube
- Eureka! Episode 7 - Weight vs. Mass
YouTube - Eureka! Episode 6 -
Gravity
Racing Balls

11. Write out each term along with its
correct description
Descriptions
• anticlockwise moments = clockwise
moments
• two boys of different weights sit opposite
each other on a see saw, both the same
distance from the pivot
• the turning effect of a force
moment balancedsystem
unbalanced
system
Lever Principle
GCSE PHYSICS:
Moments

12. Gina weighs 500N and stands on one end of a seesaw.
She is 0.5m from the pivot.
What moment does she exert?
moment = 500 x 0.5
= 250 Nm
0.5m
500N
pivot
Moment calculation

13. moment = force (N) x distance from pivot (cm or m)
The moment of a force is given by the equation:
Moments are measured in Newton centimetres (Ncm) or
Newton metres (Nm).
moment
f x d
Moment equation

14. Principle of moments
The girl on the right exerts
a clockwise moment,
which equals...
The girl on the left exerts
an anti-clockwise moment,
which equals...
her weight x her distance
from pivot
her weight x her distance
from pivot

15. Principle of moments
When something is balanced about a pivot:
total clockwise moment = total anticlockwise moment
If the anticlockwise moment and clockwise moment are
equal then the see-saw is balanced. This is known as the
principle of moments.

16. Two girls are sitting on opposite sides of on a see-saw.
One girl weighs 200N and is 1.5m from the pivot. Where
must her 150N friend sit if the seesaw is to balance?
When the see-saw is balanced:
Principle of moments –
calculation
total clockwise moment = total anticlockwise moment
200N x 1.5m = 150N x distance
200 x 1.5 = distance
150
distance of second girl = 2m

17. Anagrams

18. Tower cranes are essential at any major construction site.
load arm
trolley
loading platform
tower
Concrete counterweights are fitted to the crane’s short arm.
Why are these needed for lifting heavy loads?
counterweight
Why don’t cranes fall over?

19. Using the principle of moments, when is the crane balanced?
moment of = moment of
load counterweight
If a 10,000N counterweight is three metres from the
tower, what weight can be lifted when the loading
platform is six metres from the tower?
6m
3m
10,000N?
Why don’t cranes fall over?

20. moment of
counterweight
distance of counterweight
from tower
=
= 10,000 x 3
= 30,000 Nm
counterweight x
moment of
load
=
= ? x 6
load x distance of load from tower
moment of load = moment of counterweight
? x 6 = 30,000
? = 3,000
6
? = 5,000 N
Why don’t cranes fall over?

21. Where should the loading platform be on the loading arm
to carry each load safely?
Crane operator activity