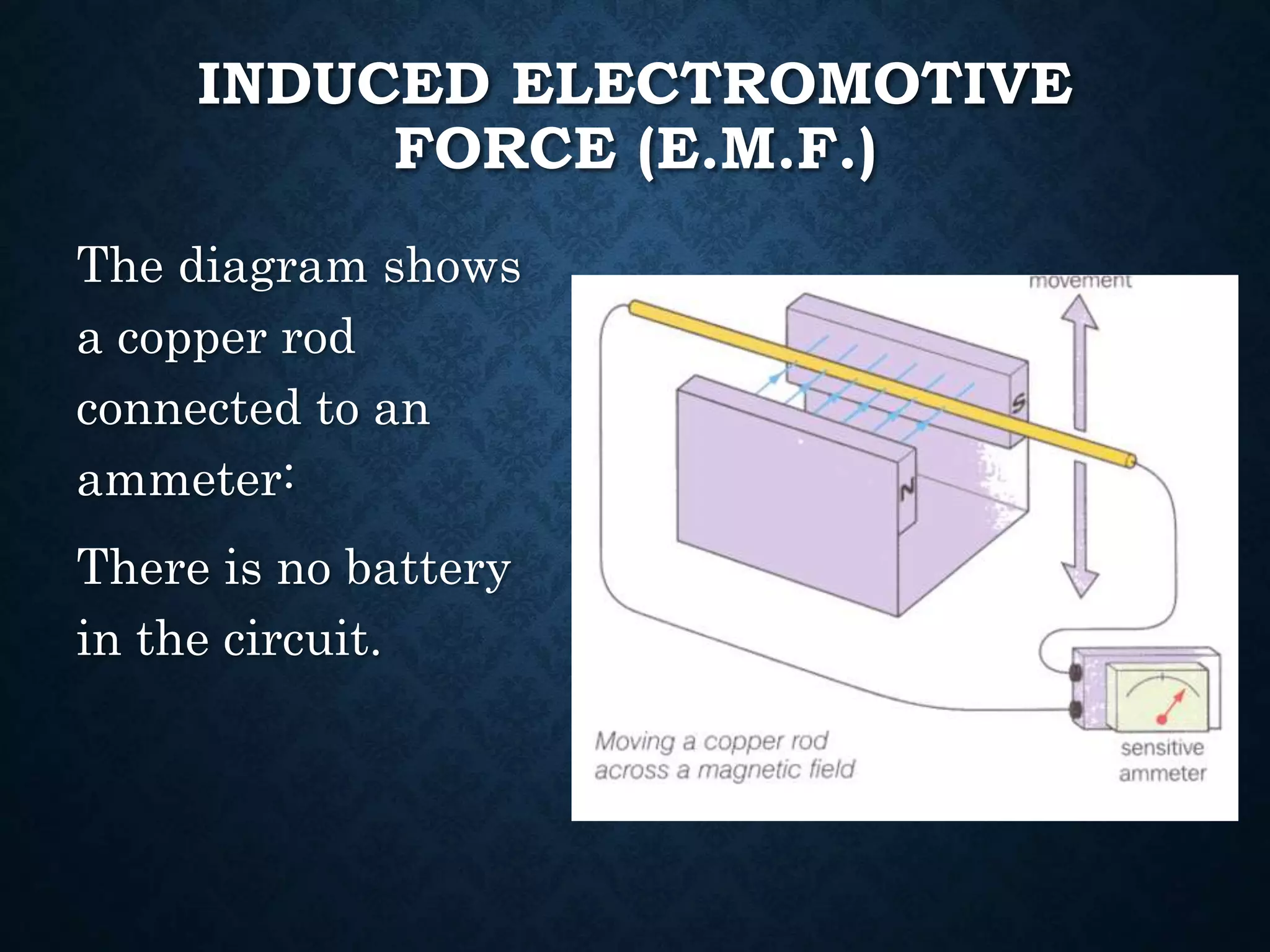
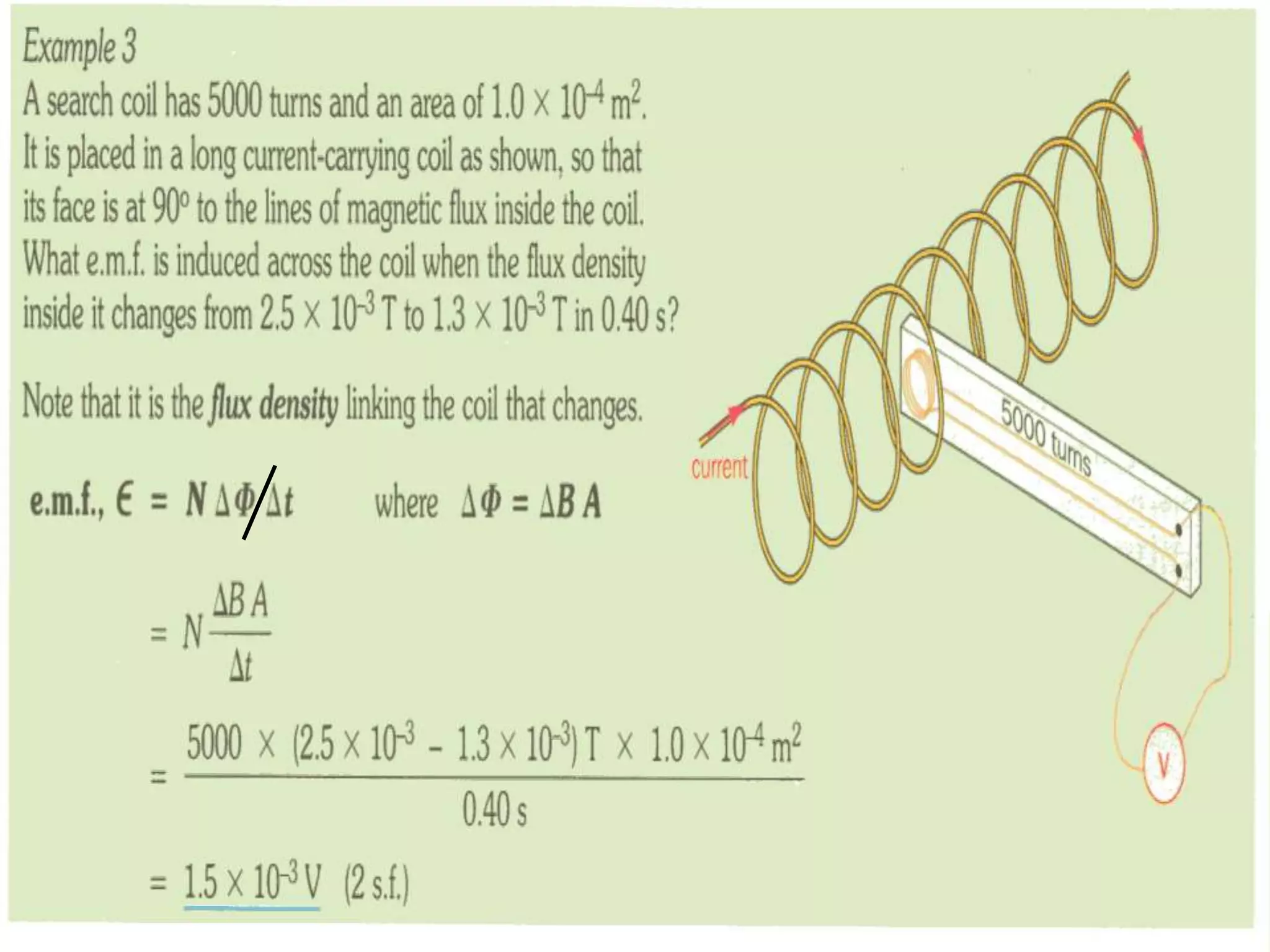
This document discusses electromagnetic induction and Faraday's law of induction. It explains that an electromotive force (emf) is induced in a conductor when it moves through a magnetic field. The direction of the induced current is determined by Lenz's law, which states that the induced emf will oppose the change in magnetic flux that creates it. Faraday's law quantifies the relationship between the induced emf and the rate of change of the magnetic flux through the conductor.

1. ELECTROMAGNETISM
Topic 11.1 Electromagnetic Induction

2. INDUCED ELECTROMOTIVE
FORCE (E.M.F.)
The diagram shows
a copper rod
connected to an
ammeter:
There is no battery
in the circuit.

3. What happens when you move the
copper rod downwards, to cut across the
horizontal magnetic field?
The pointer on the meter makes a brief
`flick' to the right, showing that an
electric current has been induced.

4. What happens when you move the rod
upwards?
The meter again gives a `flick', but this
time to the left.
You have now induced a current in the
opposite direction.

5. If you hold the rod stationary, or if you
move the rod along the field lines, there
is no induced current.

6. WHY DOES ELECTROMAGNETIC
INDUCTION OCCUR?
When you move the copper rod, its free electrons
move with it.
But when a charge moves in a magnetic field it
experiences a force on it
(the B Q v force).
You can use Flemings Left hand Rule to show
that the force on each electron is to the left as
shown in the diagram
(Remember that an electron moving down has to
be treated like a positive charge moving up.

8. So electrons accumulate at one end of
the rod, making it negative.
This leaves the other end short of
electrons and therefore positive.
There is now a voltage (potential
difference) across the ends of the
moving rod.
If the ends of the moving rod are joined
to form a complete circuit, the induced
voltage causes a current to flow round
the circuit as shown by the flick of the
ammeter.

9. The induced voltage is a source of electrical
energy - an e.m.f
When a conductor is moving in a magnetic
field like this, an e.m.f is induced, even if
there isn't a complete circuit for a current to
flow.

10. FORMULA FOR A STRAIGHT
CONDUCTOR
Consider a conductor
of length l that moves
with velocity v
perpendicular to a
magnetic flux density
or induction B as
shown in the figure.

11. When the wire conductor moves in the
magnetic field, the free electrons
experience a force because they are
caused to move with velocity v as the
conductor moves in the field.
F = e v B

12. This force causes the electrons to drift from
one end of the conductor to the other, and one
end builds-up an excess of electrons and the
other a deficiency of electrons.
This means that there is a potential
difference or emf between the ends.
Eventually, the emf becomes large enough to
balance the magnetic force and thus stop
electrons from moving.

13. evB = eE ( from F = evB and F = eE)
Therefore E = Bv
If the potential difference (emf) between the
ends of the conductor is ε then
ε = E L (from E = V/d)
By substitution we have
ε = B v L

14. MAGNETIC FLUX
The magnetic flux (Φ) through a region is a
measure of the number of lines of magnetic
force passing through that region.
Φ = AB cos θ
where A is the area of the region and θ is the
angle of movement between the magnetic
field and a line drawn perpendicular to the
area swept out.
The unit of magnetic flux is the weber Wb.

15. For a single conductor in the magnetic flux
density, it can be seen that
ε = - ΔΦ/ Δt (the rate of change of flux density)
For N number of conductors as in the case for a
solenoid, the term flux-linkage is used.
Then
ε = - N Δ (Φ/ Δt)
This is Faraday’s Law
The minus sign shows us that the emf is always
produced so as to oppose the change in flux.

16. TIME-CHANGING MAGNETIC
FLUX
Therefore the production of an emf is
produced by a time changing magnetic flux.
This could be due to the wire or coil moving
through a magnetic field
Or by an increasing or decreasing magnetic
field of an electromagnet next to a wire or
coil.

17. FARADAY’S LAW
We know that an e.m.f. is induced when there
is a change in the flux linking a conductor.
Faraday's law makes the connection between
the size of the induced e.m.f. and the rate at
which the flux is changing.
It states that:
the magnitude of the induced e.m.f is directly
proportinonal to the rate of change of
magnetic flux or flux linkage.

18. LINKING
For a single conductor in the magnetic flux
density, it can be seen that
ε = - ΔΦ/ Δt (the rate of change of flux
density)
And ε = B v l
Therefore - ΔΦ/ Δt = B v l

19. LENZ’S LAW
Faraday's law tells us the size of the induced
e.m.f., but we can find its direction using
Lenz's law
The direction of the induced e.m.f is such that
it will try to oppose the change in flux that is
producing it.

21. Lenz's law is illustrated in the diagrams: As
you move the N-pole into the coil, an e.m.f. is
induced which drives a current round the
circuit as shown.
Now use the right-hand grip rule
Can you see that the current produces a
magnetic field with a N-pole at the end of the
coil nearest to the magnet?
So the coil repels the incoming magnet, and
in this way the induced current opposes the
change in flux.

22. Why is the current reversed as you move the
N-pole out?
By Lenz's law, the coil needs to attract the
receding N-pole

23. Lenz's law is a result of the conservation of
energy. If you move the magnet into the coil,
you feel the repulsive force.
You have to do work to move the magnet
against this force.
And so energy is transferred from you (or the
system that is moving the magnet) to the
electrical energy of the current.

27. Interactive Faraday
Emf
Faraday