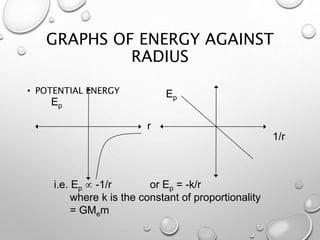
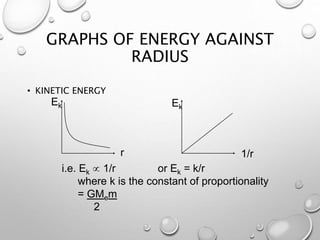
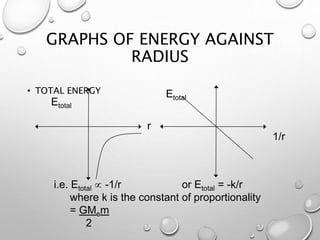
Here are the steps to solve these problems: 1) Given: Distance above earth's surface = 1000km Use equation: V = -GM/R = - (6.67x10-11 Nm2/kg2)(5.98x1024 kg)(1000km) = -6.3x1010 J/kg 2) Given: ∆V = Vf - Vi = -60 - (-20) MJ/kg = -40 MJ/kg ∆E = mg∆h = m∆V ∆V = ∆E/m = -40x106 J/kg / 50 kg = -800 m/s 3)

1. 10.2 FIELDS AT
WORK

2. GRAVITATIONAL POTENTIAL AND
STRENGTH
THE GRAVITATIONAL FIELD STRENGTH IS A
VECTOR QUANTITY WHOSE DIRECTION IS
GIVEN BY THE DIRECTION OF THE FORCE A
MASS WOULD EXPERIENCE IF PLACED AT THE
POINT OF INTEREST
G = G M
R2
COMPARE THIS TO GRAVITATIONAL
POTENTIAL
V = - G M
R
AND WE GET THE RELATIONSHIP THAT
G = -V
R

3. ELECTRIC AND
GRAVITATIONAL FIELDS.
(A) INVERSE SQUARE LAW OF FORCE
COULOMB'S LAW IS SIMILAR IN FORM TO NEWTON'S LAW
OF UNIVERSAL GRAVITATION.
BOTH ARE INVERSE SQUARE LAWS WITH CONSTANTS OF
1/(4ΠΕ) IN THE ELECTRIC CASE CORRESPONDING TO
THE GRAVITATIONAL CONSTANT G.
THE MAIN DIFFERENCE IS THAT WHILST ELECTRIC
FORCES CAN BE ATTRACTIVE OR REPULSIVE,
GRAVITATIONAL FORCES ARE ALWAYS ATTRACTIVE.
TWO TYPES OF ELECTRIC CHARGE ARE KNOWN BUT
THERE IS ONLY ONE TYPE OF GRAVITATIONAL MASS.
BY COMPARISON WITH ELECTRIC FORCES,
GRAVITATIONAL FORCES ARE EXTREMELY WEAK.

5. (B) FIELD STRENGTH
THE FIELD STRENGTH AT A POINT IN
A GRAVITATIONAL FIELD IS DEFINED
AS THE FORCE ACTING PER UNIT
MASS PLACED AT THE POINT.
THUS IF A MASS M IN KILOGRAMS
EXPERIENCES A FORCE F IN NEWTONS
AT A CERTAIN POINT IN THE EARTH'S
FIELD, THE STRENGTH OF THE FIELD
AT THAT POINT WILL BE F/M IN
NEWTONS PER KILOGRAM.

6. THIS IS ALSO THE ACCELERATION A,
THE MASS WOULD HAVE IN METRES
PER SECOND SQUARED IF IT FELL
FREELY UNDER GRAVITY AT THIS
POINT (SINCE F = MA).
THE GRAVITATIONAL FIELD STRENGTH
AND THE ACCELERATION DUE TO
GRAVITY AT A POINT THUS HAVE THE
SAME VALUE (I.E. F/M) AND THE SAME
SYMBOL, G, IS USED FOR BOTH. AT
THE EARTH'S SURFACE G = 9.8 N KG-'
= 9.8 M S-2 (VERTICALLY

9. (C) FIELD LINES AND EQUIPOTENTIALS
THESE CAN ALSO BE DRAWN TO REPRESENT
GRAVITATIONAL FIELDS BUT SUCH FIELDS
ARE SO WEAK, EVEN NEAR MASSIVE BODIES,
THAT THERE IS NO METHOD OF PLOTTING
FIELD LINES SIMILAR TO THOSE USED FOR
ELECTRIC (AND MAGNETIC) FIELDS.
FIELD LINES FOR THE EARTH ARE DIRECTED
TOWARDS ITS CENTRE AND THE FIELD IS
SPHERICALLY SYMMETRICAL.
OVER A SMALL PART OF THE EARTH'S
SURFACE THE FIELD CAN BE CONSIDERED
UNIFORM, THE LINES BEING VERTICAL,
PARALLEL AND EVENLY SPACED.

10. (D) POTENTIAL AND P.D.
ELECTRIC POTENTIALS AND PDS ARE
MEASURED IN JOULES PER COULOMB (J
C-1) OR VOLTS;
GRAVITATIONAL POTENTIALS AND PDS
ARE MEASURED IN JOULES PER
KILOGRAM (J KG-1).
AS A MASS MOVES AWAY FROM THE
EARTH THE POTENTIAL ENERGY OF THE
EARTH-MASS SYSTEM INCREASES,
TRANSFER OF ENERGY FROM SOME
OTHER SOURCE BEING NECESSARY.

11. IF INFINITY IS TAKEN AS THE ZERO
OF GRAVITATIONAL POTENTIAL (I.E.
A POINT WELL OUT IN SPACE WHERE
NO MORE ENERGY IS NEEDED FOR
THE MASS TO MOVE FURTHER AWAY
FROM THE EARTH)
THEN THE POTENTIAL ENERGY OF
THE SYSTEM WILL HAVE A NEGATIVE
VALUE EXCEPT WHEN THE MASS IS
AT INFINITY.
AT EVERY POINT IN THE EARTH'S
FIELD THE POTENTIAL IS THEREFORE
NEGATIVE (SEE EXPRESSION BELOW),
A FACT WHICH IS CHARACTERISTIC

14. ESCAPE SPEED
THE ESCAPE SPEED IS THE SPEED
REQUIRED FOR A PROJECTILE TO
LEAVE THE EARTH´S GRAVITATIONAL
ATTRACTION.
I.E. TO GET TO INFINITY!

15. IF THE POTENTIAL AT THE EARTH´S SURFACE
IS
V = - G ME
RE
THEN THE EP CHANGE TO GET TO INFINITY IS
G ME X M
RE
WHERE M IS THE MASS OF THE PROJECTILE

16. FOR THIS AMOUNT OF ENERGY TO BE
GAINED THE PROJECTILE MUST HAVE
HAD AN EQUAL AMOUNT OF EK
THEREFORE ½MV2 = G ME X M
RE
V = ( 2GME
RE )
BUT USING THE FACT THAT G = G ME
RE
2
THEN V = (2GRE )

17. DERIVING THE THIRD LAW
SUPPOSE A PLANET OF MASS M MOVES WITH SPEED V IN A
CIRCLE OF RADIUS R ROUND THE SUN OF MASS M, THE
GRAVITATIONAL ATTRACTION OF THE SUN FOR THE PLANET IS
= G MM
R2
FROM NEWTON’S LAW OF UNIVERSAL GRAVITATION
IF THIS IS THE CENTRIPETAL FORCE KEEPING THE PLANET IN
ORBIT THEN
G MM = MV2 (FROM CENTRIPETAL EQUATION)
R2 R
GM = V2
R

18. IF T IS THE TIME FOR THE PLANET TO MAKE
ONE ORBIT
V = 2 R V2 = 222 R2
T T2
GM = 4 2 R 2 R
T2
GM = 4 2 R 3
T2
R 3 = GM
T2 4 2
R 3 = A CONSTANT
T2

19. ENERGY OF ORBITING SATELLITES
POTENTIAL ENERGY, EP
A SATELLITE OF MASS M ORBITING THE EARTH AT A
DISTANCE R FROM ITS CENTRE HAS
GRAVITATIONAL POTENTIAL, V = - G ME
R
THEREFORE THE GRAVITATIONAL POTENTIAL ENERGY,
EP = - G MEM
R

20. ENERGY OF ORBITING SATELLITE
KINETIC ENERGY, EK
BY THE LAW OF UNIVERSAL GRAVITATION AND
NEWTON’S SECOND LAW
G MEM = MV2
R2 R
THEREFORE THE KINETIC ENERGY,
EK = ½MV2 = G MEM
2R

21. ENERGY OF ORBITING SATELLITE
TOTAL ENERGY, EP+ EK
TOTAL ENERGY = - G MEM + G MEM
R 2R
TOTAL ENERGY = - G MEM
2R
TOTAL ENERGY IS CONSTANT FOR A CIRCULAR
ORBIT.

22. GRAPHS OF ENERGY AGAINST
RADIUS
• POTENTIAL ENERGY Ep
1/r
Ep
r
i.e. Ep  -1/r or Ep = -k/r
where k is the constant of proportionality
= GMem

23. GRAPHS OF ENERGY AGAINST
RADIUS
• KINETIC ENERGY
Ek
1/r
Ek
r
i.e. Ek  1/r or Ek = k/r
where k is the constant of proportionality
= GMem
2

24. GRAPHS OF ENERGY AGAINST
RADIUS
• TOTAL ENERGY Etotal
1/r
Etotal
r
i.e. Etotal  -1/r or Etotal = -k/r
where k is the constant of proportionality
= GMem
2

25. 1. FIND THE GRAVITATIONAL POTENTIAL
1000KM ABOVE THE EARTH’S SURFACE?
2. A SATELLITE OF MASS 50KG MOVES FROM A
POINT WHERE THE POTENTIAL IS –20 MJKG-1 TO
ANOTHER POINT WHERE THE POTENTIAL IS –60
MJKG-1
• WHAT IS THE CHANGE IN POTENTIAL
• WHAT IS THE SPEED OF THE SATELLITE
3. A 2000KG SPACECRAFT IN ORBIT AT R ABOVE
THE EARTH OF RADIUS R. THE POTENTIAL AT
THE EARTH'S SURFACE IS –60 MJ KG-1. WHAT
IS THE CHANGE IN POTENTIAL ENERGY IF THE
SPACECRAFT RETURNS TO EARTH