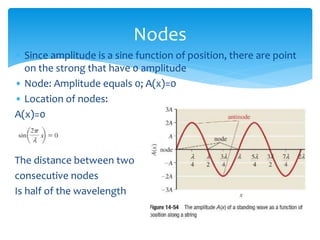
Standing waves are harmonic waves with equal amplitude, wavelength, and frequency that are moving in opposite directions. They have a phase constant of 0. Standing waves have nodes where the amplitude is 0 and antinodes where the amplitude is at a maximum of 2A. The distance between nodes is half the wavelength, as is the distance between antinodes. An example problem calculates the length of a water pipe with a standing wave pattern by determining the wavelength from the given frequency and speed, and using the node and antinode spacing to relate the length to the wavelength.

1. Standing Waves
By Brigette Wee

2.  Standing waves are harmonic waves with equal amplitude,
wavelength, and frequency that are moving in opposite
directions of each other
 Phase constant is 0 (for mathematical simplicity)
 Represented by:
 If two 2 standing waves are moving, each segment of the string
oscillates in SHM with frequency and amplitude varying along the
string
 For a string oscillating in a standing wave:
What is it?

3. • Since amplitude is a sine function of position, there are point
on the strong that have 0 amplitude
• Node: Amplitude equals 0; A(x)=0
• Location of nodes:
A(x)=0
The distance between two
consecutive nodes
Is half of the wavelength
Nodes

4. Antinodes
 Antinode: the points where it is moving at maximum
amplitude (2A)
 Location of antinodes:
The distance between two
consecutive nodes
Is half of the wavelength

5. Lets try a problem…

6.  As illustrated below, a water pipe has a standing wave
pattern with 4 nodes and 4 antinodes. The frequency of
sound is 250 Hz and a sound wave travels with a speed of
300m/s

7.  What is the length of the water tube?
Question 1

8.  Since the distance between consecutives antinodes is half a
wavelength and the distance between an adjacent node and
antinode is a quarter of a wavelength (see diagram)
 7/4(λ)= L
 So first we need to find λ:
 V=λ f
 λ =v/f=(300m/s)/(250Hz)
 λ =1.2m
 So back to 7/4(λ)= L
 L= (7/4)(1.2m)
 L=2.1m
Solution to Q1

9. Thank you for watching

10.  Physics for Scientist and Engineers An Interactive
Approach by Hawkes, Iqbal, Mansour Milner-Bolotin,
Williams
Work cited