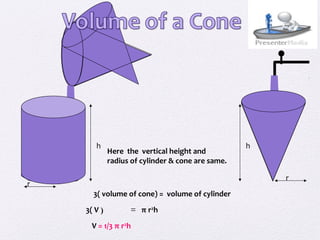
The document provides information on the volumes and surface areas of various 3D shapes including cubes, cuboids, cylinders, cones, spheres, hemispheres, and frustums. For each shape, the key formulas for calculating volume and/or surface area are presented using variables like length, width, height, radius, diameter, and slant height. Diagrams are included to illustrate the geometric features used in the formulas.

5. • opposite sides are equal
• each angle is of 900
• Diagonals are equal &bisect each other

7. SQUARE
• All sides are equal
• each angle is of 900
• Diagonals are equal & bisect each other at 900

9. CICRLE

12. Cube
Requirement
Edge/side

13. Cube
L
L
L
•Diagonal of cube=√3×L unit
•Lateral surface area=perimeter of base ×height
=4×L3 unit3
• Total surface area = 2LxL + 2LxL + 2LxL
= 6L2
• Volume = Base area x height
=LxLxL
= L3

14. Cuboid
Top
Side 2
Back
Front
Bottom
Length (L)
Side 1
Height (H)
Breadth (B)

15. Total surface Area
L
L
H
L
B
B
H
H
B
B
H
L
L
H
L
H
L
Total surface Area = L x H + B x H + L x H + B x H + L x B + L x B
= 2 LxB + 2BxH + 2LxH
= 2 ( LB + BH + LH )

16. Lateral surface area=2(L+B)H unit2
Volume=area of base×height
=L×B×H unit3
Diagonal of cuboid=√L2+B2+H2

17. Example:
7 cm
4 cm
8 cm
Here:
l=8cm
B=4cm
H=7cm
SA=2(lb+bh+lh)=2(8X4+4x7+8x7)
=2(64+56+112)
=232cm²
V = lwh
V = 8(4)(7)
V = 224 cm³

18. Curved surface area of
cylinder
Curved surface area of an object is the area of outer covering of
it. If a rectangular paper is folded ,the length becomes the
circumference and the breadth becomes the height. So csa of a
cylinder is 2πr x height.
Curved surface area of
cylinder=2πrh

19. Outer Curved Surface area of cylinder
r
Circumference of
circle = 2 π r
r
h
Formation of Cylinder by
bangles
It is the area covered by the outer surface of a cylinder.
Circumference of circle = 2 π r
Area covered by cylinder = Surface area of of cylinder = (2 π r) x( h)

20. Total Surface area of a solid cylinder
circular
surfaces
=
Area of curved surface +
=(2 π r) x( h) + 2 π r2
= 2 π r( h+ r)
Curved
surface
area of two circular surfaces

21. Other method of Finding Surface area of cylinder with the help of paper
r
h
h
2πr
Surface area of cylinder = Area of rectangle= 2 πrh

22. Here:
r=3.1
H=12
SA = 2πrh + 2πr²
SA = 2π(3.1)(12) + 2π(3.1)²
SA = 2π (37.2) + 2π(9.61)
SA = π(74.4) + π(19.2)
SA = 233.7 + 60.4
SA = 294.1 in²

24. Right Circular Cone
Requirement
Radius(r)
Height(h)
Slant height(l)
At least 2 must be given
(l)2= (h)2 + (r)2
l =√ h2 + r2

25. Surface area of cone
l
l
Area of a circle having sector (circumference) 2π l = π l 2
Area of circle having circumference 1 = π l 2/ 2 π l
So area of sector having sector 2 π r = (π l 2/ 2 π l )x 2 π r = π rl
2πr

26. h
Here the vertical height and
radius of cylinder & cone are same.
h
r
r
3( volume of cone) = volume of cylinder
3( V )
= π r2h
V = 1/3 π r2h

27. if both cylinder and cone have same height and radius then volume of a cylinder is
three times the volume of a cone ,
Volume = 3V
Volume =V

29. Mr. Mohan has only a little jar of juice he wants to distribute it to
his three friends. This time he choose the cone shaped glass so
that quantity of juice seem to appreciable.

34. Sphere
Requirement
Radius(r)
Height = diameter

35. If we make a cone having radius and height equal to the radius of sphere. Then a
water filled cone can fill the sphere in 4 times.
r
r
r
V=1/3 πr2h
V1
If h = r then
V=1/3 πr3
V1 = 4V = 4(1/3 πr3)
= 4/3 πr3

36. Click to See the
experiment
Volume of a Sphere
h=r
r
Here the vertical height and
radius of cone are same as radius
of sphere.
r
4( volume of cone) = volume of Sphere
4( 1/3πr2h ) = 4( 1/3πr3 ) = V
V = 4/3 π r3

39. Hemisphere
Requirement
Radius/ diameter
Height=radius

41. Frustum of Cone
Volume
V = π/12 h (D2 + D d + d2) (9a)
m = ( ( (D - d) / 2 )2 + h2)1/2 (9c)

46. Bottle
Cone
shape
Cylindrical
shape

52. Hollow Cylinder
Volume
V = π/4 h (D2 - d2) (5)

53. TRIANGULAR
PRISM
To find the surface
area of a triangular
prism you need to be
able to imagine that
you can take the
prism apart like so:
Notice there are TWO congruent triangles
and THREE rectangles. The rectangles may
or may not all be the same.
Find each area, then add.

54. Example:
Find the AREA of each SURFACE
1. Top or bottom triangle:
8mm
A = ½ bh
A = ½ (6)(6)
9mm
A = 18
2. The two dark sides are the same.
A = lw
A = 6(9)
6 mm
6mm
3. The back rectangle is
different
A = 54
ADD THEM ALL UP!
18 + 18 + 54 + 54 + 72
A = lw
A = 8(9)
A = 72
SA = 216 mm²

55. PYRAMID
Volume
V = 1/3 h A
1
(6)
where
A1 = area of base (m2, ft2)
h = perpendicular height of pyramid (m,
ft)
Surface
A = ∑ sum of areas of triangles forming sides
+A
b
(6b)
where
the surface areas of the triangular faces will
have different formulas for different shaped

56. FRUSTUM OF PYRAMID
VOLUME
V = h/3 ( A1 + A2 + (A1 A2)1/2) (7)

57. Zone of SPHERE
V = π/6 h (3a2 + 3b2 + h) (11a)
Am = 2 π r h (11b)
A0 = π (2 r h + a2 + b2) (11c)

58. V = π/6 h (3/4 s2 + h2)
= π h2 (r - h/3) (12a)
Am = 2 π r h
= π/4 (s2 + 4 h2) (12b)

59. V = 2/3 π r2 h (13a)
A0 = π/2 r (4 h + s) (13b)

60. V = π/6 h (14a)
A0 = 4 π ((R + r) (R - r))
3
3
= 2 π h (R + r) (14b)
h = 2 (R2 - r2)1/2 (14c)
1/2

61. V = 2/3 π R
2
h (15a)
A0 = 2 π R (h + (R2 - h2/4)1/2)
h = 2 (R2 - r2)1/2 (15c)
(15b)

62. V = π2/4 D d2 (16a)
A0 = π2 D d (16b)

63. V = 2/3 r2 h (18a)
Am = 2 r h (18b)
A0 = Am + π/2 r2 + π/2 r (r2 +
2 1/2

64. V = π/4 d2 h
(17a)
Am = π d h (17b)
A0 = π r (h1 + h2 + r + (r2 + (h1 2
1/2

65. V ≈ π/12 h (2 D2 + d2)
(19a)

66. Volume
V = A1 h (3a)
where
A1 = side area (m2, ft2)