Downloaded 298 times
![Problems based on
Perimeter and area of a circle
21 cm
Converting 1.32 Km into cm, we get,
1.32 Km = 1.32 x 1000 m [∵ 1 Km = 1000 m]
= 1.32 x 1000 x 100 cm [∵1m = 100 cm]
= 132000 cm
Chapter : Areas Related To Circles Website: www.letstute.com](https://image.slidesharecdn.com/areasrelatedtocircles-perimeterandareaofacircle-140826050125-phpapp02/75/Areas-related-to-circles-Perimeter-and-area-of-a-circle-for-class-10-maths-7-2048.jpg)
Uploaded byLet's Tute
Areas related to circles - Perimeter and area of a circle for class 10 maths.
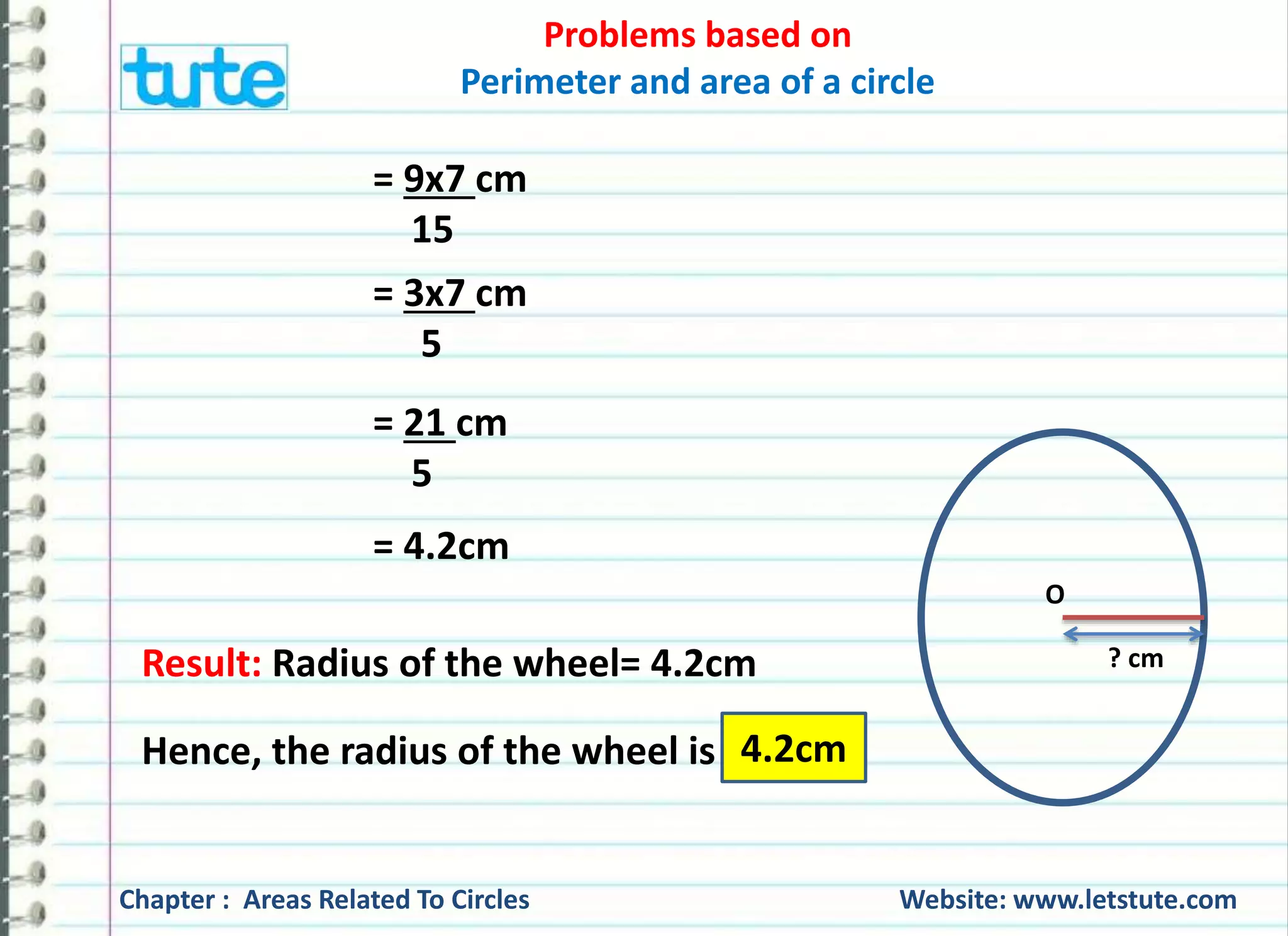
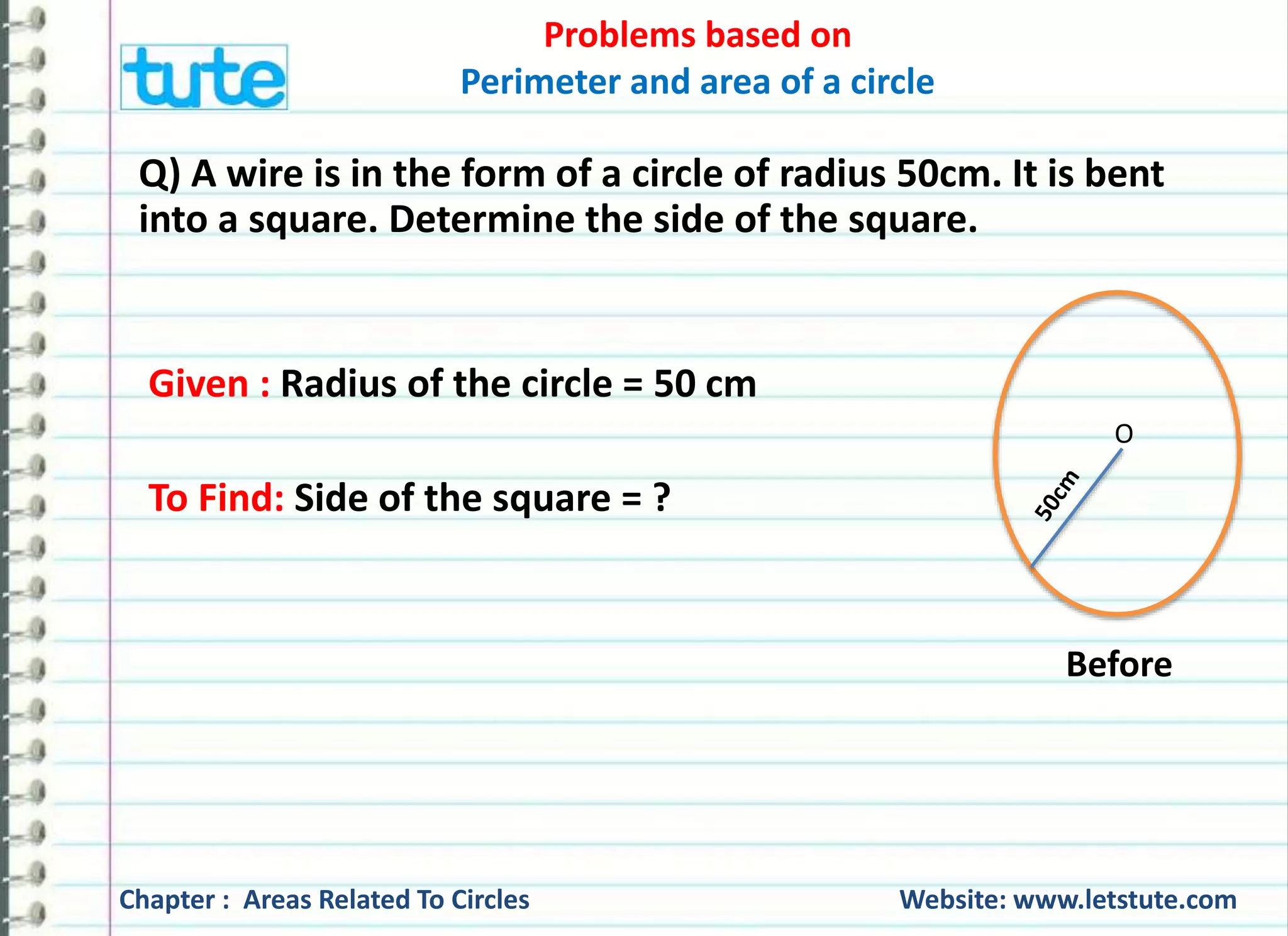
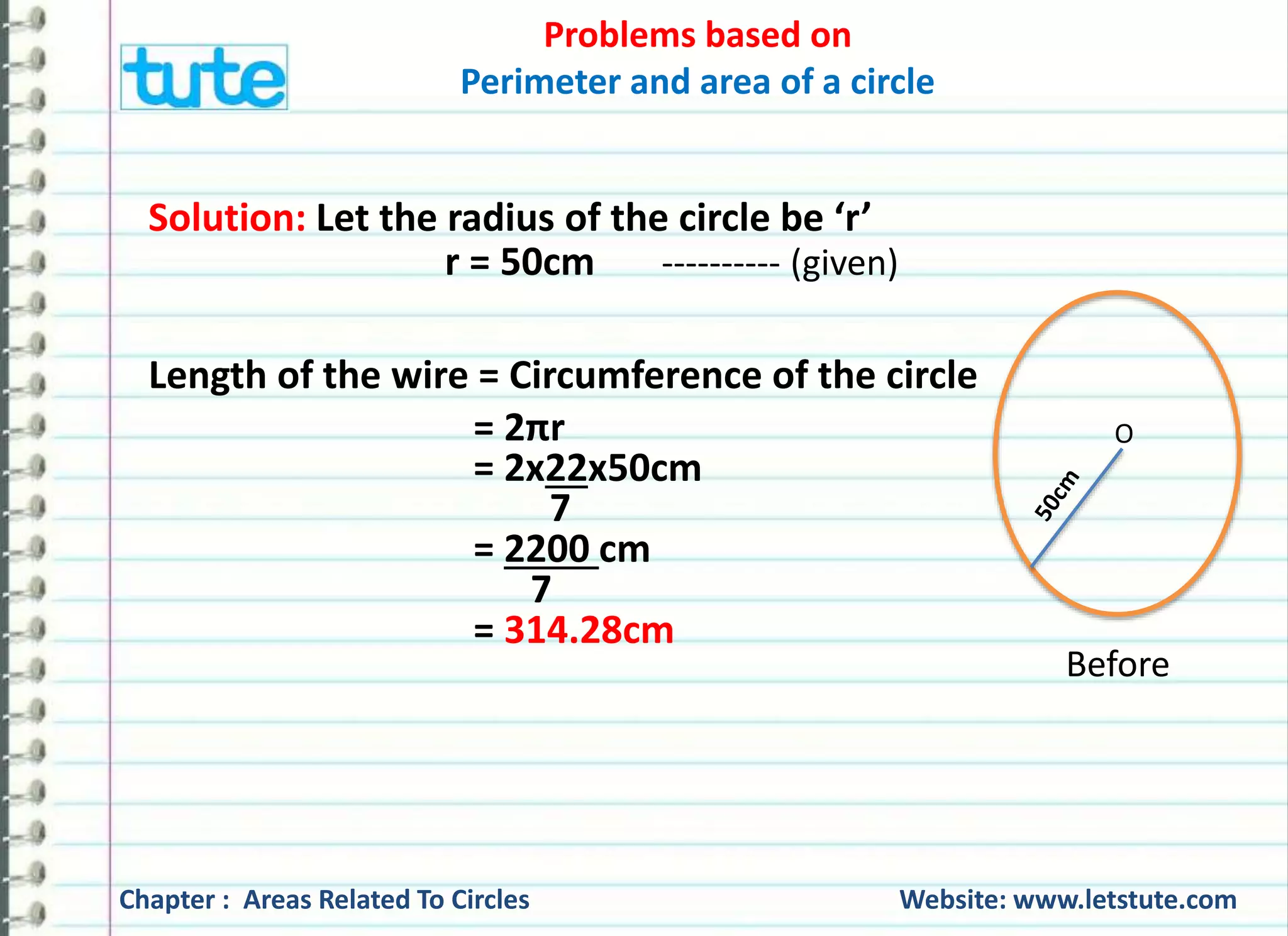
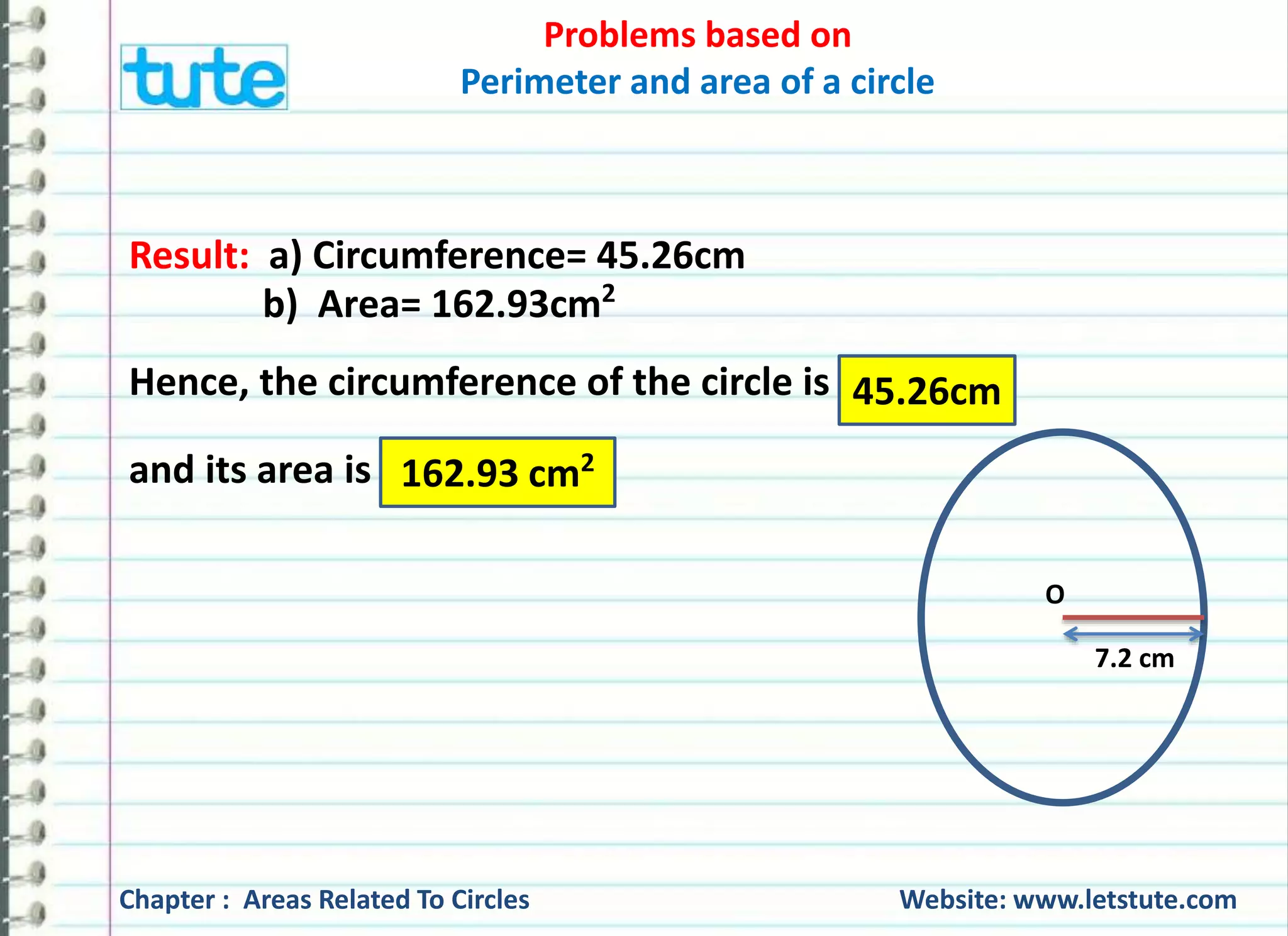
The document covers various problems related to the perimeter and area of circles, providing solutions for finding the radius of a wheel based on the number of rotations and distance covered, as well as calculating the number of revolutions for a cart wheel. It also computes the speed of a bicycle wheel given its diameter and revolutions per second, and it explores the relationship between the radius when the perimeter and area of a circle are equal. The content emphasizes practical applications of geometry in real-life scenarios.
More Related Content
Similar to Areas related to circles - Perimeter and area of a circle for class 10 maths.
Areas related to circles - Perimeter and area of a circle for class 10 maths.
- 1. Areas Related ToCircles Problems based on Perimeter and area of a circle Chapter : Areas Related To Circles Website: www.letstute.com
- 2. Problems based on Perimeter and area of a circle Q) A wheel rotates 25000 times to cover a distance of 90 km. Find its radius. Given: Rotation of the wheel = 25000 times Distance covered = 90 km by the wheel To find: Radius of the wheel = ? ? Chapter : Areas Related To Circles Website: www.letstute.com
- 3. Problems based on Perimeter and area of a circle Solution: Let ‘r’ be the radius of the wheel. ? Circumference of the wheel = Distance covered in one rotation. = 90 Km 2πr ∵ ퟗퟎ 퐊퐦= 90 x 1000 x 100 cm = 9000000 25000 = 360 cm 2πr = 360 cm Chapter : Areas Related To Circles Website: www.letstute.com
- 4. Problems based on Perimeter and area of a circle 2 x 22 x r = 360cm r = 360x7 cm 2x22 = 180 x 7 22 = 90 x 7 11 = 630 11 r = 57.27 cm 7 Hence, the radius of the wheel is 57.27cm ? Chapter : Areas Related To Circles Website: www.letstute.com
- 5. Problems based on Perimeter and area of a circle Q) The diameter of a cart wheel is 21 cm. How many revolutions will it make in moving 1.32 km? 21 cm Given: Diameter of the cart wheel = 21 cm To Find: Number of revolutions = ? made in 1.32 Km Chapter : Areas Related To Circles Website: www.letstute.com
- 6. Problems based on Perimeter and area of a circle Solution: Let the radius of the cart wheel be ’r’. Thus, r = Diameter = 21 cm 2 2 Circumference of the cart wheel = 2πr = 2x22x21cm 7 2 = 462 7 = 66 cm 21 cm Chapter : Areas Related To Circles Website: www.letstute.com
- 7. Problems based on Perimeter and area of a circle 21 cm Converting 1.32 Km into cm, we get, 1.32 Km = 1.32 x 1000 m [∵ 1 Km = 1000 m] = 1.32 x 1000 x 100 cm [∵1m = 100 cm] = 132000 cm Chapter : Areas Related To Circles Website: www.letstute.com
- 8. Problems based on Perimeter and area of a circle Number of revolutions = Total distance covered Circumference (Distance covered by 1 round of the cart wheel) = 132000 cm 66 cm = 12000 6 2000 21 cm = Hence, the cart wheel will make 2000 revolutions in moving 1.32 km. Chapter : Areas Related To Circles Website: www.letstute.com
- 9. Problems based on Perimeter and area of a circle Q) A wheel of a bicycle makes 6 revolutions per second. If the diameter of the wheel is 80 cm, find its speed. Given: Number of revolutions per second = 6 Diameter = 80cm To find: Speed = ? Formula: Speed = Distance Time Chapter : Areas Related To Circles Website: www.letstute.com
- 10. Problems based on Perimeter and area of a circle Solution: Let the radius of the wheel be denoted as ‘r’. Thus, r = Diameter = 80 = 40 cm 2 2 Circumference of the wheel = 2 πr = 2x22x 40 cm 7 = 1760 7 = 251.42cm Chapter : Areas Related To Circles Website: www.letstute.com
- 11. Problems based on Perimeter and area of a circle Distance covered in 1 revolution = circumference = 251.42cm Distance covered in 6 revolutions = 6 x Distance covered in 1 revolution = 6 x 251.42 cm = 1508.52 cm Since, 1 m = 100 cm ?m = 1508.52 cm = 1508.52 cm 100 = 15.08 m ∵ 15.08 m = 1508.52 cm Chapter : Areas Related To Circles Website: www.letstute.com
- 12. Problems based on Perimeter and area of a circle Speed = Distance Time = 15.08 m 1 second Result: Speed = 15.08 m/second Hence, the speed of the wheel is 15.08m/second. Chapter : Areas Related To Circles Website: www.letstute.com
- 13. Problems based on Perimeter and area of a circle Q) Find the radius of the circle whose perimeter and area are numerically equal. Given: Perimeter and the area of the circle are equal To Find: Radius of the circle = ? Solution: Let ‘r’ be the radius of the circle. Then, its area = πr2 and its perimeter = 2πr It is given that the area of the circle is numerically equal to its perimeter. Chapter : Areas Related To Circles Website: www.letstute.com
- 14. Problems based on Perimeter and area of a circle Thus, πr2 = 2πr πr2 - 2πr = 0 πr(r-2) = 0 Either πr = 0 or r-2 = 0 r = 0 (rejected) or r = 2 Hence, the radius of the circle is 2 units Chapter : Areas Related To Circles Website: www.letstute.com
- 15. Visit us on– www.letstute.com Subscribe us on www.youtube.com/letstute Thank you
Editor's Notes
- #3 Let us take a look at the first question, A tyre rotates 25000 times to cover a distance of 90 km. Find its radius. In this questn, we have been given that the tyre rotates 25000 times covering a distance of 90 km What we need to find is the radius of the tyre.
- #4 Lets see the solution, Firstly, let r be the radius, We know that, circum of the wheel is = to distance cov in 1 rotan We also know the formula for circum which is 2 pir r. the distance vovered in 1 rotatn is 360 cm. We get 360 cm in the follow manner, We nned to convert 90 km into cm, = 9 x 1000 x 100 cm = 9000000 25000 which is the no. of tyms the wheel rotates = 360 cm
- #5 By substituting, pie byu 22/7, we get
- #10 The next question says that, A wheel of a bicycle makes 6 revolutions per second. If the diameter of the wheel is 80 cm, find its speed. Lets see what is given to us, We have been given, no. of revolutions per second which r 6 And the diameter which is 80 cm We need to find out the speed. Now, do you know the formula for speed??? The formula is speed = dist/ time
- #11 Let us see the solution,
- #12 Now, we need to find the distance covered in 4 revolutions…. Since distance covered by 1 revolution is 251.42 cm , the distance covered by 6 revolutions is 6x 251.42 cm =1508.52 cm = 15.08 m Now finally………we can find the speed which is distance / time =15.08 m 1 second =15.08x18 km/h (18/5 is obtained by conerrting meter/sec intio km/hr= 60x60= 18/5 5 100 =54.28 km/h
- #14 Let us take a look at the next question, The question says that Find the radius of the circle whose perimeter and area are numerically equal. In this question we have been given, that the perimeter and the area of the circle are equal. We need to find the radius of the circle. Lets us come to the solution. Let us first represent r to be the radius of the circle. We know that the area of the circle is πr2 and its perimeter = 2πr We have be given that the area of the circle is equal to its perimeter.
- #15 Thus, by using the formulas we get, πr2 = 2πr By taking 2pie r on LHS, we get, πr2 - 2πr = 0 By taking pie r common, we get, πr(r-2) = 0 Now, Either πr = 0 or r-2 = 0 But pie r cannot be 0 as for it to be 0, r should b 0 since we know that pie is 22/7, In a circle r can never be 0. thus r = 0 is rejected. Thus, r = 2 Hence………………..