Dokumen ini membahas konsep dasar rangkaian arus bolak-balik satu fase, mencakup hubungan fase antara arus dan tegangan serta penjumlahan fasor. Mahasiswa diharapkan dapat menggambarkan diagram fasor dan menghitung total tegangan pada rangkaian. Selain itu, dijelaskan juga tentang rangkaian resistif, induktif, dan kapasitif serta perhitungan reaktansi dan daya pada rangkaian-rangkaian tersebut.

1. Politeknik Negeri Malang
Unit 4
24
Rangkaian Arus Bolak-balik Satu Fase.
Tujuan
Setelah selesai mempelajari bagian ini, mahasiswa diharapkan akan mampu :
 Menjelaskan hubungan fase antara arus dan tegangan.
 Menggambarkan hubungan fase tegangan dan arus bolak-balik dalam bentuk
gelombang dan diagram fasor.
 Menghitung penjumlahan fasor.
4.1 Diagram Fasor
Arus dan tegangan bolak-balik, dan hubungan fase antara keduanya, dapat digambarkan
dengan menggunakan gelombang sinus, tapi metode ini kurang praktis. Metode yang
lebih sederhana adalah dengan menggunakan diagram fasor. Fasor (vektor) adalah garis
lurus yang mempunyai arah dan panjang tertentu. Diagram di mana garis ini digunakan
untuk menyatakan arus, tegangan gelombang sinus, dan hubungan fasenya disebut
diagram fasor.
Tegangan
Arus
Beda fasa
(a) Diagram bentuk gelombang
Tegangan
(b) Diagram Fasor
Arus
(c) Fasor
Gambar 4.1. Konvensi pada arus bolak-balik
Gambar 4.1(b) memperlihatkan diagram fasor pada kondisi sefase.
06. TeoriListrik Terapan
Abdul Manaf
1/7/2014

2. Politeknik Negeri Malang
25
Pada beberapa rangkaian, kurva arus dan tegangan tidak mencapai harga nol dan
maksimum secara bersamaan, oleh karena itu dikatakan bahwa arus dan tegangan tidak
sefase, dan sudut mendahului atau tertinggal antara tegangan dan arus disebut sudut fase
(simbol φ).
Gambar 4.2 (a) memperlihatkan arus yang tertinggal dari tegangan sebesar 30° dan
Gambar 4.2 (b) memperlihatkan kondisi yang sama dengan menggunakan diagram fasor.
Tegangan
Arus
Beda fasa
Gambar 2.2. Arus tertinggal dari tegangan (lagging)
(a) Diagram bentuk gelombang
(b) Diagram fasor
Gambar 4.2. Arus tertinggal dari tegangan (lagging)
Gambar 4.3(a) memperlihatkan arus yang mendahului tegangan sebesar 30° dan Gambar
4.3(b) memperlihatkan kondisi yang sama dengan menggunakan diagram fasor.
Tegangan
Arus
Beda fasa
(a) Diagram bentuk gelombang
(b) Diagram fasor
Gambar 4.3. Arus mendahului tegangan (leading)
06. TeoriListrik Terapan
Abdul Manaf
1/7/2014

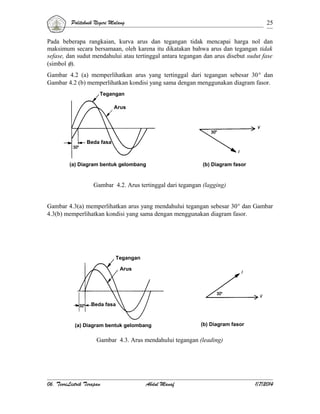
3. Politeknik Negeri Malang
26
4.2 Penjumlahan Fasor
Harga arus atau tegangan bolak-balik tidak dapat dijumlahkan secara aritmetika kecuali
mereka sefase. Jika dua gaya gerak listrik (ggl) atau tegangan bolak balik dihubungkan
seri, keduanya mungkin tidak sefase satu sama lain. Tegangan total dapat ditemukan
dengan cara menjumlahkan kedua ggl dengan cara seperti yang diperlihatkan di Gambar
4.4 (a).
Metode yang lebih sederhana adalah dengan menggambar kedua fasor dengan
menggunakan harga r.m.s. untuk ggl dan kemudian jumlahkan keduanya dengan
menggunakan metode paralelogram seperti yang diperlihatkan di Gambar 4.4 (b).
Tegangan Vtotal di Gambar 4.4 (b) adalah sebanding dengan harga r.m.s. Vtotal kurva
gelombang sinus di Gambar 4.4 (a).
Waktu
(a) Diagram bentuk gelombang
(b) Diagram fasor
Gambar 4.4. Penambahan harga arus bolak-balik
Contoh 1
Dua tegangan A dan B dihubungkan seri. Tegangan A sebesar 150 V mendahului arus
sebesar 45°. Tegangan B sebesar 100 V tertinggal dari arus sebesar 30°. Tentukan ggl
total dan sudut fasenya
Karena dua tegangan seri, arus digunakan sebagai fasor acuan.
Untuk membuat diagram fasor, ikuti langkah berikut:
Langkah 1
Gambar fasor arus secara horizontal ke kanan sebagai fasor referensi [Gambar 4.5(a)].
Langkah 2
06. TeoriListrik Terapan
Abdul Manaf
1/7/2014

4. Politeknik Negeri Malang
27
Gambar fasors untuk VA dan VB dan ukur skala serta sudut fase dari fasor acuan [Gambar
4.5(b)].
(a) Fasor Referensi
Skala : 1 mm mewakili 2,5 V
(b) Menggambar fasor tegangan
(c) Menjumlahkan fasor
Gambar 4.5. Fasor untuk contoh 1
Langkah 3
Buat paralelogram fasor dan tentukan ggl total dan sudut fase dari resultan [Gambar
4.5(c)]. Dengan mengukur panjang Vtotal dan sudutnya terhadap referensi maka diperoleh :
Tegangan total = 201 V
Sudut faseφ
= 17° mendahului
Dari contoh 1 dan contoh 2 tampak bahwa dengan menggunakan cara grafis atau
matematis akan menghasilkan nilai yang sama.
4.3 Rangkaian Resistif Murni
06. TeoriListrik Terapan
Abdul Manaf
1/7/2014

5. Politeknik Negeri Malang
28
Suatu rangkaian arus bolak balik terdiri dari tahanan (resistansi) murni R ohm
dihubungkan pada tegangan sinusoida v = Vm sin ωt seperti yang ditunjukkan dalam
Gambar 4.6.
Gambar 4.6
Rangkaian resistif murni pada arus bolak balik
Tegangan
Arus
(a) Gambar rangkaian
(b) Gambar gelombang
(c) Diagram fasor
Jika tegangan diberikan dengan persamaan
v = Vm sin ωt
Maka arus yang melewati R adalah :
iR =
V Vmax sin Wt
=
R
R
iR =
Vmax
SinWt = I max SinWt
R
dimana Im =
Vmax
R
Apabila dibagi dengan √2, diperoleh Im/√2 = Vm/√2 x 1/R
Jadi I = V/R
Di mana V dan I adalah harga efektif tegangan dan arus.
Pada rangkaian resistif murni, arus tetap sefase dengan tegangan seperti yang ditunjukkan
secara grafis dalam Gambar 4.6(b) dan secara vektoris dalam Gambar 4.6(c).
4.4 Daya pada Rangkaian Resistif
Daya sesaat yang disalurkan ke rangkaian adalah hasil kali harga sesaat tegangan v dan
arus i, maka p = v.i. Dengan cara mengambil hasil perkalian v dan i untuk sejumlah
waktu tertentu, kita akan dapat menggambar kurva daya untuk satu siklus lengkap.
Contoh 3
Tegangan sinusoida mempunyai Vmaks = 2 V dihubungkan ke resistansi sebesar 2 Ω.
Gambar kurva untuk memperlihatkan harga daya yang diserap oleh resistor pada waktu
tertentu selama satu siklus.
06. TeoriListrik Terapan
Abdul Manaf
1/7/2014

6. Politeknik Negeri Malang
29
Langkah pertama adalah dengan mempersiapkan suatu tabel yang memperlihatkan harga
v, i dan P untuk siklus rotasi antara 0°E dan 360°E. Karena Vmaks = 2 V dan R = 2 Ω ,
maka Imaks = 1 A (lihat Tabel 4-1).
Tabel 4.1
Harga sesaat yang terhitung untuk contoh 3
Sudut θ
0°
30°
60°
90°
120°
150°
180°
210°
240°
270°
300°
330°
360°
v =Vmaks sin θ
0
1,0
1,73
2,0
1,73
1,0
0
-1,0
-1,73
-2,0
-1,73
-1,0
0
i = Imak sin θ
0
0.5
0,87
1,0
0,87
0,5
0
-0.5
-0,87
-1,0
-0,87
-0.5
0
P = v.i.
0
0,5
1,5
2.0
1,5
0,5
0
0,5
1,5
2,0
1,5
0,5
0
Kurva untuk tegangan, arus dan daya dapat dilihat pada Gambar 2.7. Dari gambar
tersebut dapat kita simpulkan, untuk rangkaian resistif murni :
1. Kurva daya mempunyai bentuk sinusoida
2. Tidak ada daya yang mempunyai harga negatif.
3. Garis horizontal yang digambar 1 unit putus-putus di atas sumbu x membentuk sumbu
kurva daya dan mewakili harga rata-rata daya selama siklus. Daya rata-rata yang
diserap oleh resistor sebesar 1 watt.
4. Kurva daya menyelesaikan dua siklus untuk masing-masing satu siklus arus atau
tegangan atau frekuensi kurva daya adalah dua kali frekuensi tegangan/arus saluran.
Jika diambil harga Ir.m.s. dan Vr.m.s.:
Irms = 0,707 Imaks
= 0,707 x 1
= 0,707 A
Vrms = 0,707 Vmaks
= 0,707 x 2
= 1,414 V
Hasil perkalian Irms dan Vrms = 1,414 x 0,707
=1W
06. TeoriListrik Terapan
Abdul Manaf
1/7/2014

7. Politeknik Negeri Malang
30
Daya rata-rata
Gambar 4.7. Daya yang diserap oleh resistor murni pada rangkaian ac.
Daya rata-rata = Vrms x Irms
P = VI atau P =
V2
atau P = I 2 R,
R
Untuk bentuk gelombang sinus, harus diingat bahwa jika harga puncak yang digunakan
untuk menghitung daya yang digunakan, harga daya rata-rata yang diperoleh selalu
sebesar setengah dari harga daya puncak.
Yaitu, daya rata-rata = ½ daya sesaat maksimum.
Untuk bentuk gelombang sinus.
Daya rata-rata = Vr.m.s. x Ir.m.s.
karena harga rms gelombang = 0.707 dari harga puncak.
maka, Vr.m.s. = 0,707 x Vmaks dan Ir.m.s. = 0,707 x Imaks
Dengan memasukkan nilai diatas pada persamaan daya diperoleh:
P = 0,707 x Vmaks x 0,707 x Imaks = 0,5Pmaks
4.5 Rangkaian Induktif Murni
Gambar 4.8(b) memperlihatkan hubungan antara arus, ggl induksi dan tegangan pencatu
pada rangkaian induktif murni.
Gambar 4.8(c) memperlihatkan hubungan fase antara tegangan dan arus. Dengan
menggunakan fasor tegangan sebagai acuan, fasor arus tertinggal 90° di belakangnya
06. TeoriListrik Terapan
Abdul Manaf
1/7/2014

8. Politeknik Negeri Malang
31
Tegangan sumber
Tegangan induksi
arus
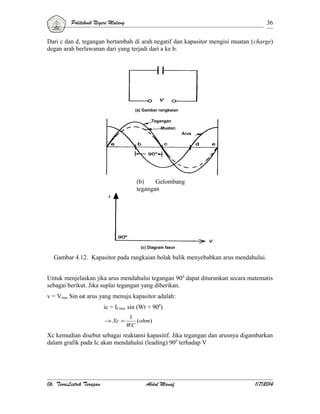
(a) Gambar rangkaian
(b) Gambar gelombang
(c) Diagram fasor
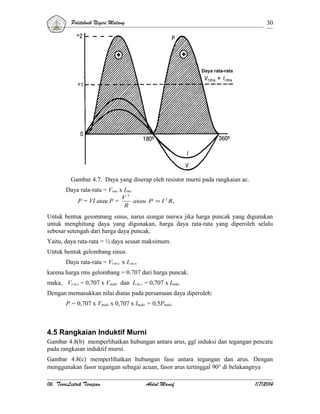
Gambar 4.8. Arus dan tegangan rangkaian induktif murni pada arus bolak-balik.
Hubungan antara tegangan dan arus yang lewat pada suatu induktor murni dapat di
uraikan dengan matematika berikut.
Tegangan yang diberikan v = Vmax Sin ωt arus yang lewat induktor adalah.
iL =
i
V (Wt ).α t
L∫
αi
di turunkan dari : Vi = L
αt
αi =
αi =
1
V2 α t
L
1
V2 α t
L∫
iL =
i
i
∫Vmax SinWt.αWt w
L
iL =
Vmax
L
iL =
Vmax
[ − Cos Wt ]
L
iL =
V max
Sin(Wt − 90 0 )
WL
∫ SinWt.αWt
i
w
i L = I lim ax Sin(Wt − 90 0 )
Dimana I 2 max =
Vmax Vmax
=
WL
XL
Akhirnya XL disebut sebagai reaktansi induktif.
06. TeoriListrik Terapan
Abdul Manaf
1/7/2014

9. Politeknik Negeri Malang
32
Jika tegangan v = Vmax Sin ωt dan iL= Imax Sin (ωt-900) maka arus tertingal 900 terhadap
tegangannya
4.6 Reaktansi Induktif
Hukum Ohm menyatakan bahwa arus sebanding dengan tegangan dibagi dengan
perlawanan arus. Reaktansi induktif adalah jenis perlawanan aliran arus, sehingga
Untuk induktansi murni
I =
V
XL
Harga reaktansi induktif pada rangkaian tergantung pada induktansi dan besar perubahan
aliran arus, yang selanjutnya akan tergantung pada frekuensi pencatu. Reaktansi induktif
dapat dihitung dari rumus berikut:
XL = 2πfL
di mana
f = frekuensi dalam hertz
L = induktansi dalam henry
Contoh 4
Sebuah kumparan memiliki induktansi sebesar 0,05 H. Berapakah reaktansi induktif pada
frekuensi (a) 25Hz, (b) 50 Hz, dan (c), pada frekuensi berapa kumparan memiliki
reaktansi sebesar 10 Ω?
(a) XL = 2πfL = 2π x 25 x 0.05 = 7,85 Ω.
(b) XL = 2π x 50 x 0.05 = 15,7 Ω.
(c) XL = 2πfL
∴f =
XL
10
=
= 31,8 Hz
2πL
2π x 0,05
Contoh 5
Supply sebesar 230 V, 50 Hz dihubungkan kumparan redam (choke) dengan resistansi
diabaikan dan arus yang melalui kumparan sebesar 2,5 A. Tentukan induktansi kumparan
I=
V
XL
V
230
∴ XL = I = 2,5 = 92 Ω
92 = 2π x 50 x L
06. TeoriListrik Terapan
Abdul Manaf
1/7/2014

10. Politeknik Negeri Malang
33
92
∴ L = 2π x 50
= 0,293 H
4.7 Induktor Seri
Dengan menghubungkan induktor secara seri, reaktansi induktif total bertambah dengan
cara yang sama seperti kita menghubungkan resistor seri, yang akan menambah resistansi
total (Gambar 4.9).
XLtotal = XL1 + XL2 + ….
Karena harga total emf induksi bertambah, maka induktansi total bertambah. Oleh karena
itu induktansi total dapat kita peroleh dengan cara yang sama.
Ltotal = L1 + L2 +….
Gambar 4.9. Dua induktor seri
4.8 Induktor Paralel
Gambar 4.10 menunjukkan rangkaian dua induktor murni yang dihubungan secara
paralel.
Contoh :
06. TeoriListrik Terapan
Abdul Manaf
1/7/2014

11. Politeknik Negeri Malang
34
Gambar 4.10. Dua induktor paralel
Dua induktor, masing-masing dengan reaktansi induktif sebesar 10 Ω, dihubungkan
paralel pada pencatu 240 V, 50 Hz. berapakah total reaktansi induktif?
I1 =
V
240
=
= 24 A ( = I 2 )
X L1
10
Masing-masing arus tertinggal dari tegangan sebesar 90°. Maka keduanya sefase satu
sama lain dan dapat ditambahkan secara aritmetika.
Itotal = I1 + I2 = 24 + 24 = 48 A
∴X Ltotal =
V
240
=
=5Ω
I tota
48
Metode yang lebih langsung dan sederhana adalah dengan menggunakan rumus yang
sama seperti resistor paralel.
1
X Ltotal
1
X Ltotal
=
1
1
1
+
+
+ ...
X L1
X L2
X L3
=
1
1
1
+
=
10
10
5
∴ XLtotal = 5 Ω
Metode yang sama digunakan untuk menentukan induktansi total rangkaian yang
dihubungkan paralel.
1
Ltotal
=
1
1
+
+...
L1
L2
4.9 Daya pada Rangkaian Induktif
Gambar 4.11 juga memperlihatkan bahwa gelombang daya adalah sinusoida jika
tegangan dan arus adalah sinusoida, tapi bahwa frekuensi gelombang daya dua kali dari
frekuensi saluran.
06. TeoriListrik Terapan
Abdul Manaf
1/7/2014

12. Politeknik Negeri Malang
35
Gambar 4.11. Daya yang digunakan oleh induktor murni pada rangkaian ac
4.10 Rangkaian Kapasitif Murni
Gambar 4.12(a) memperlihatkan rangkaian kapasitor yang dihubungkan ke catu ac. Arus
selalu mengalir secara bergantian masuk ke dalam dan keluar kapasitor ketika kapasitor
dimuati, dikosongkan, dimuati lagi dengan arah berlawanan dan dikosongkan lagi.
Gambar 4.12 (b) dan (c) menunjukkan bahwa arus mendahului 900 terhadap tegangan.
06. TeoriListrik Terapan
Abdul Manaf
1/7/2014

13. Politeknik Negeri Malang
36
Dari c dan d, tegangan bertambah di arah negatif dan kapasitor mengisi muatan (charge)
degan arah berlawanan dari yang terjadi dari a ke b.
(a) Gambar rangkaian
Tegangan
Muatan
Arus
(b)
Gelombang
tegangan
(c) Diagram fasor
Gambar 4.12. Kapasitor pada rangkaian bolak balik menyebabkan arus mendahului.
Untuk menjelaskan jika arus mendahului tegangan 900 dapat diturunkan secara matematis
sebagai berikut. Jika suplai tegangan yang diberikan.
v = Vmax Sin ωt arus yang menuju kapasitor adalah:
ic = ICmax sin (Wt + 900)
→ Xc =
1
(ohm)
WC
Xc kemudian disebut sebagai reaktansi kapasitif. Jika tegangan dan arusnya digambarkan
dalam grafik pada Ic akan mendahului (leading) 900 terhadap V
06. TeoriListrik Terapan
Abdul Manaf
1/7/2014

14. Politeknik Negeri Malang
37
4.11 Reaktansi Kapasitif
Reaktansi kapasitif adalah perlawanan yang diberikan oleh kapasitor terhadap aliran arus.
Simbol untuk reaktansi kapasitif adalah XC dan satuannya adalah ohm.
XC =
1
2π
fC
di mana XC = reaktansi kapasitif dalam ohm
f = frekuensi dalam hertz
C = kapasitansi dalam farad
Rumus di atas sering dinyatakan sebagai:
10 6
2π
fC
XC =
di mana
C = kapasitansi dalam mikrofarad.
Contoh 8
Hitung arus yang ditarik dari sumber bila kapasitor 16 µF dihubungkan ke pencatu
sebesar 240 V, 50 Hz
XC =
=
1
2π
fC
10 6
2 x π x 50 x 16
= 198,9 Ω
I =
V
Xc
240
= 198,9
= 1,2 A
4.12 Kapasitor Seri
Jika dua kapasitor dihubungkan seri, kapasitansi totalnya berkurang. Pada sumber
pencatu bolak-balik, hal ini secara efektif menambah perlawanan terhadap arus dalam
pola yang serupa dengan resistor yang dihubungkan seri
06. TeoriListrik Terapan
Abdul Manaf
1/7/2014

15. Politeknik Negeri Malang
yaitu,
38
Xctotal = Xc1 + Xc2 + …
Contoh 9
Tentukan reaktansi kapasitif dan arus yang mengalir pada sebuah kapasitor sebesar 8µF
yang dihubungkan ke pencatu 100 V, 50 Hz. Jika rangkaian ini dihubungkan seri dengan
kapasitor lain yang berkapasitas sama, tentukan arus baru yang mengalir.
Xc =
I=
1
2π
fC
=
10 6
= 397,89 Ω
2π x 50 x 8
V
Xc
=
100
= 0,25 A
397,9
Xctotal = Xc1 + Xc2 = 397,89 + 397,89 = 795,8 Ω
I=
V
=
X c total
100
= 0,125 A
795,8
4.13 Kapasitor Paralel
Kapasitor paralel pada rangkaian bolak-balik memiliki karakteristik yang sama seperti
resistor paralel. Masing-masing lintasan paralel menggunakan arus sesuai dengan
perlawanannya terhadap aliran arus.
Perlawanan total terhadap arus untuk rangkaian paralel adalah:
1
X ctotal
=
1
1
+
+ ...
X c1
X c2
Pada contoh berikut kapasitor dan tegangan pencatu yang sama dengan yang digunakan
pada contoh 9 sehingga hasilnya dapat kita bandingkan.
Contoh 10
Dua kapasitor 8 µF dihubungkan paralel ke pencatu 100 V, 50 Hz. Tentukan arus yang
mengalir melalui masing-masing kapasitor dan arus total yang mengalir
Xc =
1
10 6
=
= 397,89 Ω
2π
fC
2π x 50 x 8
06. TeoriListrik Terapan
Abdul Manaf
1/7/2014

16. Politeknik Negeri Malang
39
V
100
=
= 0,25 A
Xc
397,89
1
1
1
1
=
+
=
+
X c1
X c2
397,89
397,89
I=
1
X ctotal
= 5,026 x 10 −3
maka:
Xctotal = 198,94 Ω
V
I= X
c
=
total
100
= 0.50 A
198,94
4.14 Daya pada Rangkaian Kapasitif
Daya yang digunakan oleh kapasitor murni pada waktu tertentu sebanding dengan hasil
perkalian harga sesaat tegangan dan arus (lihat Gambar 4.13).
Gambar 4.13. Daya yang digunakan oleh arus bolak-balik induktor murni
Selama seperempat siklus pertama, kurva daya ada di sisi positif. Daya diambil dari
pencatu untuk membentuk medan magnet.
Di seperempat siklus berikutnya, tegangan turun ke nol, dan medan elektrostatis
menghilang. Energi di dalamnya kembali melewati lempeng dan kembali ke pencatu.
Ketika arahnya dibalik, daya dikembalikan. Kurva diperlihatkan pada sisi negatif gambar,
sehingga daya yang dikembalikan ini disebut daya negatif.
Di seperempat ke tiga, terdapat daya positif lagi dan medan elektrostatis terbentuk.
Siklus ke empat memperlihatkan daya yang dikembalikan.
06. TeoriListrik Terapan
Abdul Manaf
1/7/2014

17. Politeknik Negeri Malang
40
Luas kurva daya di atas garis nol sama dengan luas kurva di bawah garis nol. Sama
seperti pada rangkaian induktif murni, daya rata-rata di rangkaian kapasitif murni adalah
nol.
Soal–Soal Latihan
1. Sebuah capasitor 30mF dihubungkan pada tegangan sumber 400 volt 50Hz,
hitunglah:
a. Reaktansi kapasitive
b. Besarnya arus yang mengalir
2. .Suatu induktor murni dengan induktansi 0,2H dihubungkan pada sumber
tegangan 100 volt AC. Carilah besarnya arus yang mengalir jika frekwensi yang
bekerja sebesar:
a. 30 hertz
b. 500 hertz
4.15 Rangkaian R-L Seri
Dalam rangkaian seri, arus untuk semua bagian rangkaian adalah sama dan tegangan
keseluruhan rangkaian adalah jumlah phasor masing-masing tegangan jatuh (voltage
drop).
Gambar 4.14. Rangkaian R-L seri
Pada Gambar 4.14, tegangan jatuh pada resistor VR adalah sefase dengan arus. Tegangan
jatuh pada induktor murni VL berbeda fase 90° dengan arus.
Karena rangkaiannya seri, arus digunakan sebagai phasor acuan dan phasor tegangan
digambar seperti yang digambar di Gambar 4.15 dengan VL mendahului I sebesar 90°.
Resultan dua tegangan VR dan VL mewakili tegangan total V, dan sudut φ mewakili
perbedaan fase antara tegangan dan arus (tegangan mendahului arus sebesar φ).
06. TeoriListrik Terapan
Abdul Manaf
1/7/2014

18. Politeknik Negeri Malang
41
Gambar 4.15. Diagram phasor untuk rangkaian yang berisi resistansi
dan induktansi seri
Gambar 4.16 menunjukkan satu penggunaan praktis induktor di rangkaian arus bolakbalik. Rangkaian ini adalah rangkaian untuk mengurangi pencatu 240 V sampai ke 110 V
untuk lampu proyektor dengan sedikit kehilangan daya dan panas yang dihasilkan.
Gambar 4.16. Induktor seri dengan lampu pijar
Tegangan VR sefase dengan arus dan harga V, VR dan VL dapat diperoleh dengan
mengukurnya menggunakan voltmeter. Dengan menggunakan harga ini, dapat dibuat
diagram phasor seperti yang ditampilkan di Gambar 4.15. Karena induktor tidak murni,
tegangan tidak mendahului arus sebesar 90°, tapi sebuah sudut kurang dari 90° (sebut
saja φL) dan tegangan VRL adalah tegangan jatuh pada resistansi gulungan.
06. TeoriListrik Terapan
Abdul Manaf
1/7/2014

19. Politeknik Negeri Malang
42
4.16 Rangkaian R-C Seri
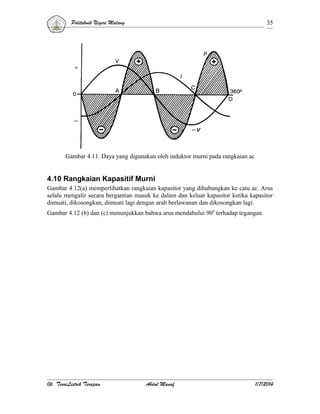
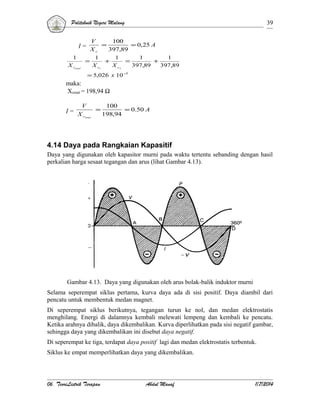
Jika arus melalui rangkaian R-C seri [Gambar 4.17(a)], akan menyebabkan tegangan
jatuh VR (karena resistansi) yang sefase dengan arus, dan tegangan jatuh VC (karena
reaktansi kapasitif) yang tertinggal dari arus sebesar 90°. Tegangan total V adalah jumlah
phasor dua tegangan jatuh VR dan VC seperti yang diperlihatkan di Gambar 2.17(b). Arus
mendahului tegangan dengan sudut φ.
(a) Gambar rangkaian
(b) Diagram phasor
Gambar 4.17. Rangkaian RC seri.
Kapasitor yang dibuat untuk tujuan komersial dianggap sebagai kapasitansi murni untuk
semua tujuan praktis dan masalah kerugian kerugian seperti yang muncul pada rangkaian
R-L seri umumnya tidak terjadi.
06. TeoriListrik Terapan
Abdul Manaf
1/7/2014

20. Politeknik Negeri Malang
43
4.17 Rangkaian R-C Paralel
Gambar 4.18 memperlihatkan rangkaian R-C paralel. Untuk tujuan praktis, arus resistor
IR sefase dengan tegangan V dan arus kapasitor mendahului keduanya sebesar 90°. Arus
total adalah jumlah phasor dua arus tersebut dan mendahului V sebesar φ.
(a) Gambar rangkaian
(b) Diagram phasor
Gambar 4.18. Rangkaian paralel R-C
4.18 Rangkaian R-L-C Seri
Pada Gambar 4.19 (a), tegangan VR sefase dengan arus, VL mendahului arus sebesar
90° dan VC tertinggal dari arus sebesar 90°.
Dua tegangan VL dan VC berbeda fase 180° satu dengan yang lain, maka tegangan jatuh
pada reaktansi, total adalah VL – VC seperti yang diperlihatkan Gambar 4.19(b). Tegangan
total V adalah jumlah phasor VR dan (VL – VC) dan φ adalah sudut fase, dengan arus
tertinggal dari tegangan sebesar φ°. Jika VC lebih besar daripada VL, arus dapat
mendahului tegangan dengan sudut tertentu.
06. TeoriListrik Terapan
Abdul Manaf
1/7/2014

21. Politeknik Negeri Malang
44
(a) Gambar rangkaian
(b) Diagram phasor
Gambar 4.19. Rangkaian seri R-L-C
4.19 Impedansi Rangkaian Seri (Segitiga Impedansi)
Phasor tegangan di Gambar 4.20(a) dapat juga digambarkan seperti Gambar 4.20(b).
(a) Diagram phasor
(b) Segitiga
Gambar 4.20. Menggunakan segitiga tegangan dalam diagram phasor
Tegangan jatuh masing-masing dapat dinyatakan sebagai faktor arus:
yaitu,
V = IZ, VR = IR dan VL = IXL.
Karena harga arus sama untuk masing-masing komponen, segitiga di Gambar 4.20(b)
dapat juga mewakili R, XL dan Z, seperti Gambar 4.21.
06. TeoriListrik Terapan
Abdul Manaf
1/7/2014

22. Politeknik Negeri Malang
45
Karena ini adalah segitiga siku-siku, maka dapat kita gunakan teori Pythagoras:
yaitu
Z2 = R2 + XL2.
Z = R2 + X L
2
Hanya untuk
rangkaian seri
Gambar 4.21. Segitiga impedansi
Dalam rangkaian R-L-C seri, reaktansi efektif adalah (XL – XC).
Dalam hal ini, maka:
Z =
R2 + (X L − X C )2
Jika XC memiliki harga yang lebih besar daripada X L, maka harga XL – XC akan bernilai
negatif. Namun, hal ini tidak berpengaruh pada harga Z karena nilai negatif jika
dikuadratkan akan menjadi nilai positif.
Reaktansi kapasitif akan menghasilkan arus yang mendahului tegangan sebesar 90°.
Reaktansi induktif akan menghasilkan arus yang tertinggal dari tegangan sebesar 90°.
Jika harga reaktansi kapasitif dan induktif sama, keduanya akan menghilangkan satu
sama lain, dan hanya meninggalkan resistansi sebagai komponen rangkaian yang efektif.
Dalam kondisi ini, rangkaian disebut dalam kondisi resonansi. Rangkaian kemudian
berlaku sebagai rangkaian resistansi murni.
Contoh 11
.Sebuah resistansi sebesar 30 Ω dihubungkan seri dengan reaktansi induktif sebesar 60 Ω
dan reaktansi kapasitif sebesar 20 Ω. Berapakah impedansi rangkaian?
06. TeoriListrik Terapan
Abdul Manaf
1/7/2014

23. Politeknik Negeri Malang
Z =
46
R 2 + ( X L − X C )2
= 30 2 + (60 − 20) 2
= 900 +1600
= 2500
=50Ω
Gambar 4.22. Diagram untuk Contoh 11
Contoh 12
Rangkaian di Gambar 4.23 dihubungkan ke pencatu 240 V, 50 Hz. Tentukan impedansi
rangkaian, arus yang mengalir dan sudut fasenya.
Gambar 4.23. Diagram rangkaian untuk Contoh 12
R = 20 Ω
XL = 2πfL = 2π x 50 x 0,05 = 78,5 Ω.
1
10 6
Xc = 2π = 2 x π x 50 x 80 = 39,8 Ω
fC
Z =
R2 + ( X L − X C )2
=
20 2 + (78,5 −39,8) 2
=
400 +1500
= 46,3 Ω
06. TeoriListrik Terapan
Abdul Manaf
1/7/2014

24. Politeknik Negeri Malang
47
V
240
=
= 5,5 A
Z
43,6
R
20
cos φ =
=
= 0,459
Z
43,6
∴φ = 62,7° (arus tertinggal dari tegangan sebesar 62,7°).
I =
Soal Latihan :
1.
Suatu circuit memiliki hambatan 12 ohm induktansi 0,15 H dan capasitor 10omF
dihubungkan secara seri dan diberi sumber tegangan 100volt, 50hertz.
Hitunglah:
a)
impedeansi.
b)
arus yang mengalir
c)
tegangan dari masing-masing elemen
d)
beda phasa satuan arus dan tegangan sumbernya
2.
Suatu circuit disusun seri mempunyai hambatan 4Ω induktansi 0,5A. Serta
capasitor 20,3mF diberi sumber tegangan 100 volt 50 Hz hitunglah tegangan dari
masing-masing elemen dan gambarkan diagram phasornya.
3.
suatu circuit terdiri dari R1, L dan R2 dihubungnkan secara seri, arus yang
mengalir sebesar 6,5A dengan sumber tegangan 220 volt 50Hz. Tegangan masingmasing elemen adalah 65 volt, 12 volt, dan 149 volt. Tentukan besarnya masingmasing elemen dan gambarkan phasor diagramnya.
4.
Suatu hambatan murni dihubungkan seri dengan sebuah kumparan.diberi
tegangan sumber 230 volt 50 Hz arus yang mengalir 1,8 A tegangan pada
hambatan 80volt sedang pada kumparan 170volt carilah nilai dari masing-masing
elemen
06. TeoriListrik Terapan
Abdul Manaf
1/7/2014

25. Politeknik Negeri Malang
48
4.20 Rangkaian R-L Paralel
Dalam rangkaian paralel, tegangan mempunyai nilai yang sama pada semua bagian
paralel dan arus total merupakan penjumlahan phasor masing-masing arus yang melewati
bagian paralel. (lihat Gambar 4.24 (a)).
(a) Gambar rangkaian
(b) Diagram phasor
Gambar 4.24. Rangkaian paralel R-L
Tegangan V digunakan sebagai phasor acuan untuk menggambar diagram phasor.
Anggaplah R dan L adalah komponen murni: IR sefase dengan V; IL tertinggal dari V
sekitar 90°; Itotal adalah hasil penjumlahan phasor IR dan IL [seperti yang ditunjukkan di
Gambar 2.24(b), di mana Itotal tertinggal dari V sebesar φ).
06. TeoriListrik Terapan
Abdul Manaf
1/7/2014

26. Politeknik Negeri Malang
49
4.21 Rangkaian R-L-C Paralel
Total arus yang mengalir dalam rangkaian jenis ini sama dengan jumlah phasor phasor IR,
IL dan IC (lihat Gambar 4.25). Jika L dan C adalah komponen murni, dua arus IL dan IC
berbeda fase sebesar 180° dan karena itu dapat dikurangi (yaitu IL – IC). Dalam hal ini
Itotal tertinggal dari tegangan sebesar φ. Harga IC yang lebih besar dapat menyebabkan arus
total mendahului tegangan yang digunakan.
(b) Diagram phasor
(a) Gambar rangkaian
Gambar 4.25. Rangkaian paralel R-L-C
4.22 Impedansi Rangkaian Paralel
Dalam menentukan impedansi di rangkaian paralel, tentukan harga arus total terlebih
dahulu dan gunakan hukum Ohm:
impedansi =
tegangan yang digunakan
, yaitu , Z = V/I .
arus total
Metode segitiga impedansi untuk rangkaian seri tidak dapat dan tidak boleh kita gunakan
dalam rangkaian paralel.
Metode untuk menentukan impedansi rangkaian paralel diilustrasikan di contoh 13.
06. TeoriListrik Terapan
Abdul Manaf
1/7/2014