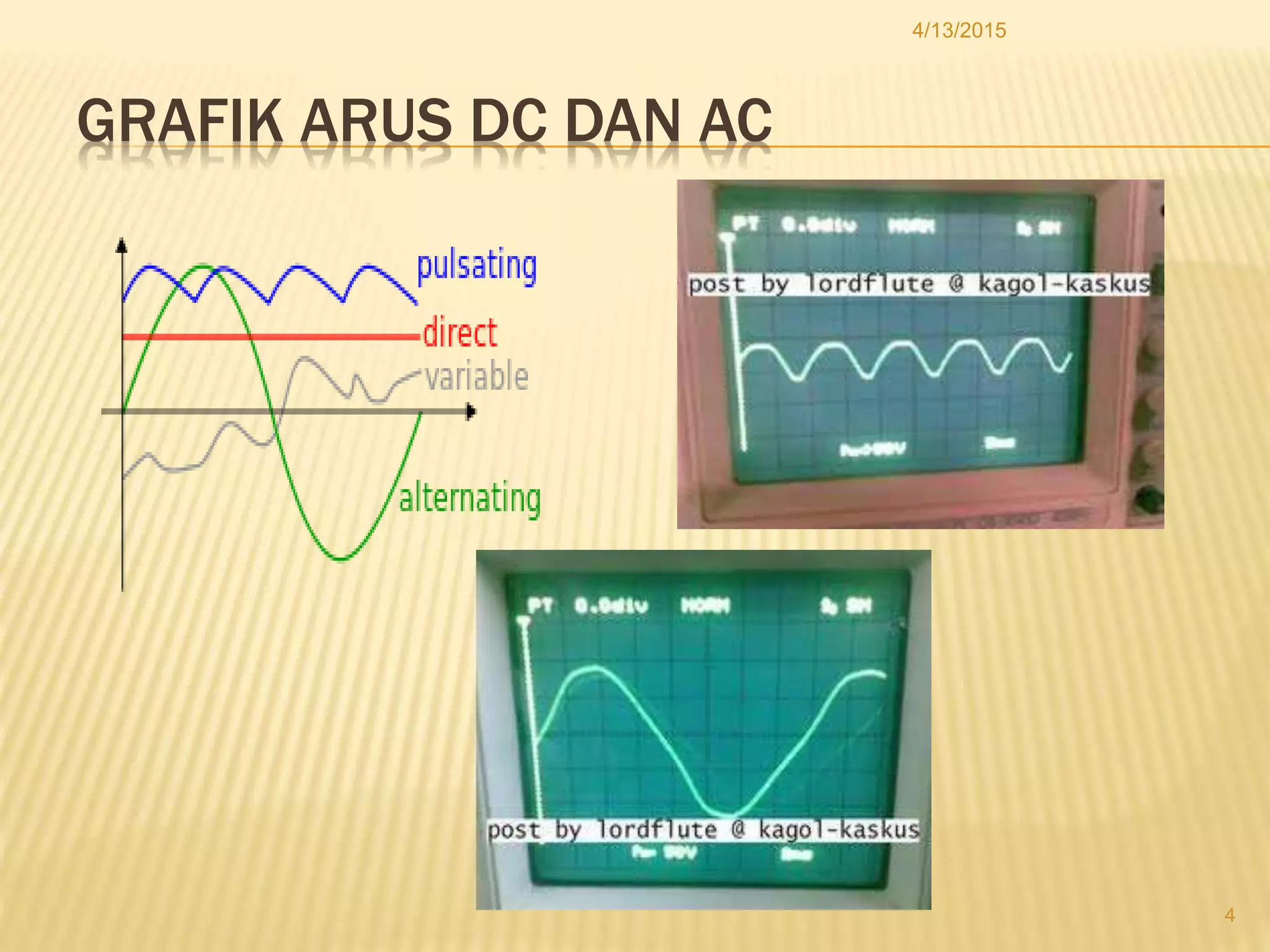
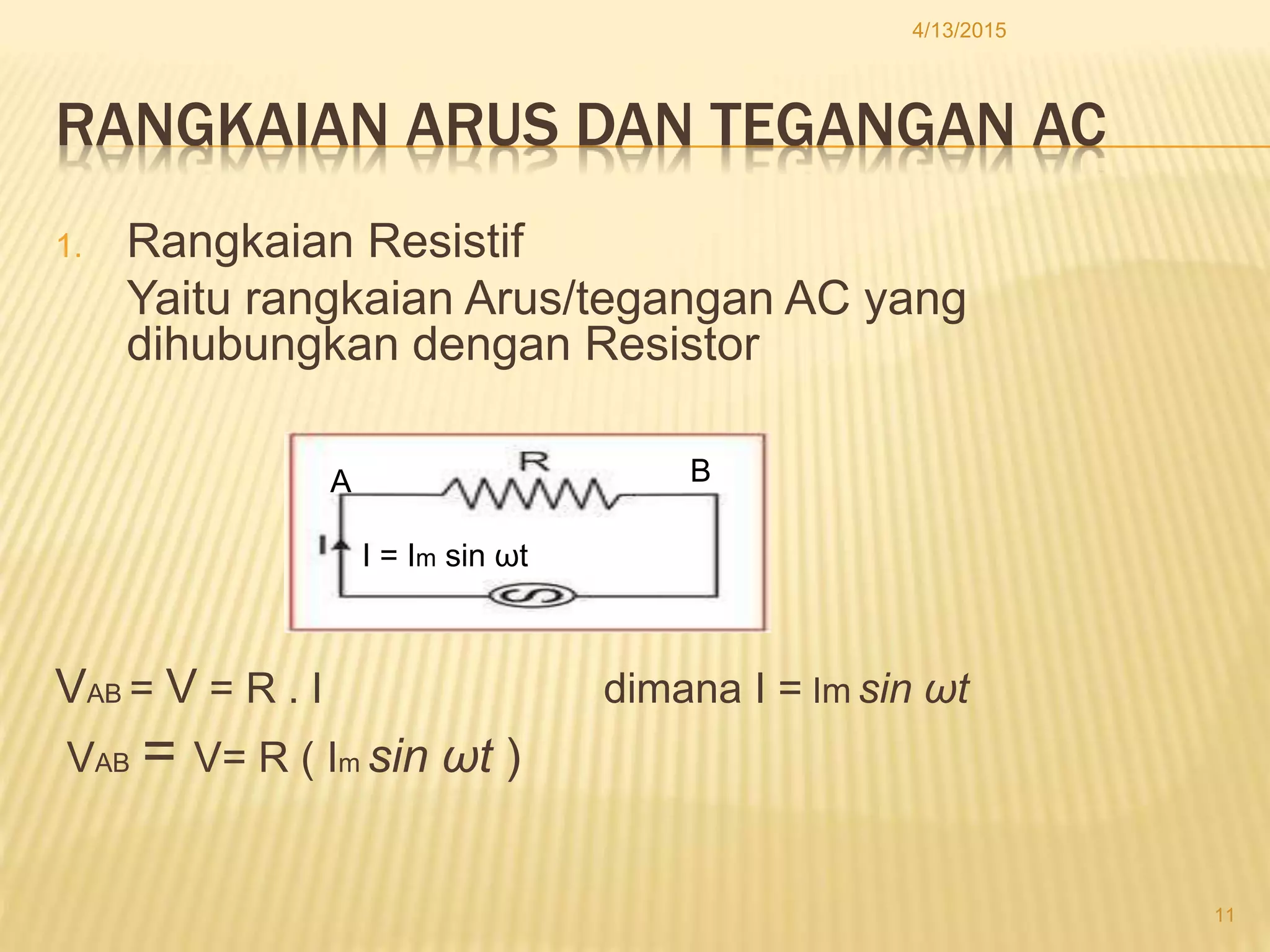
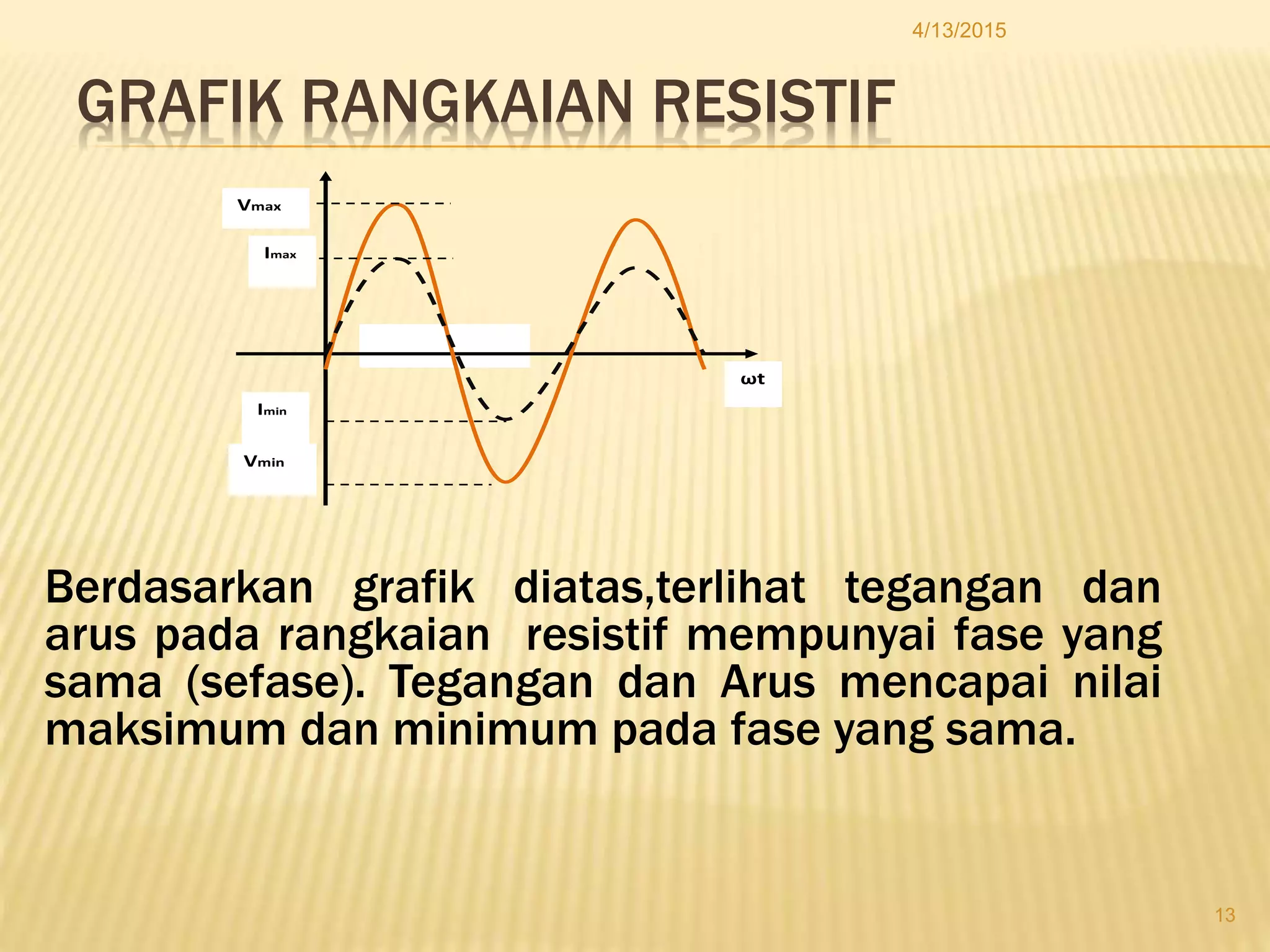
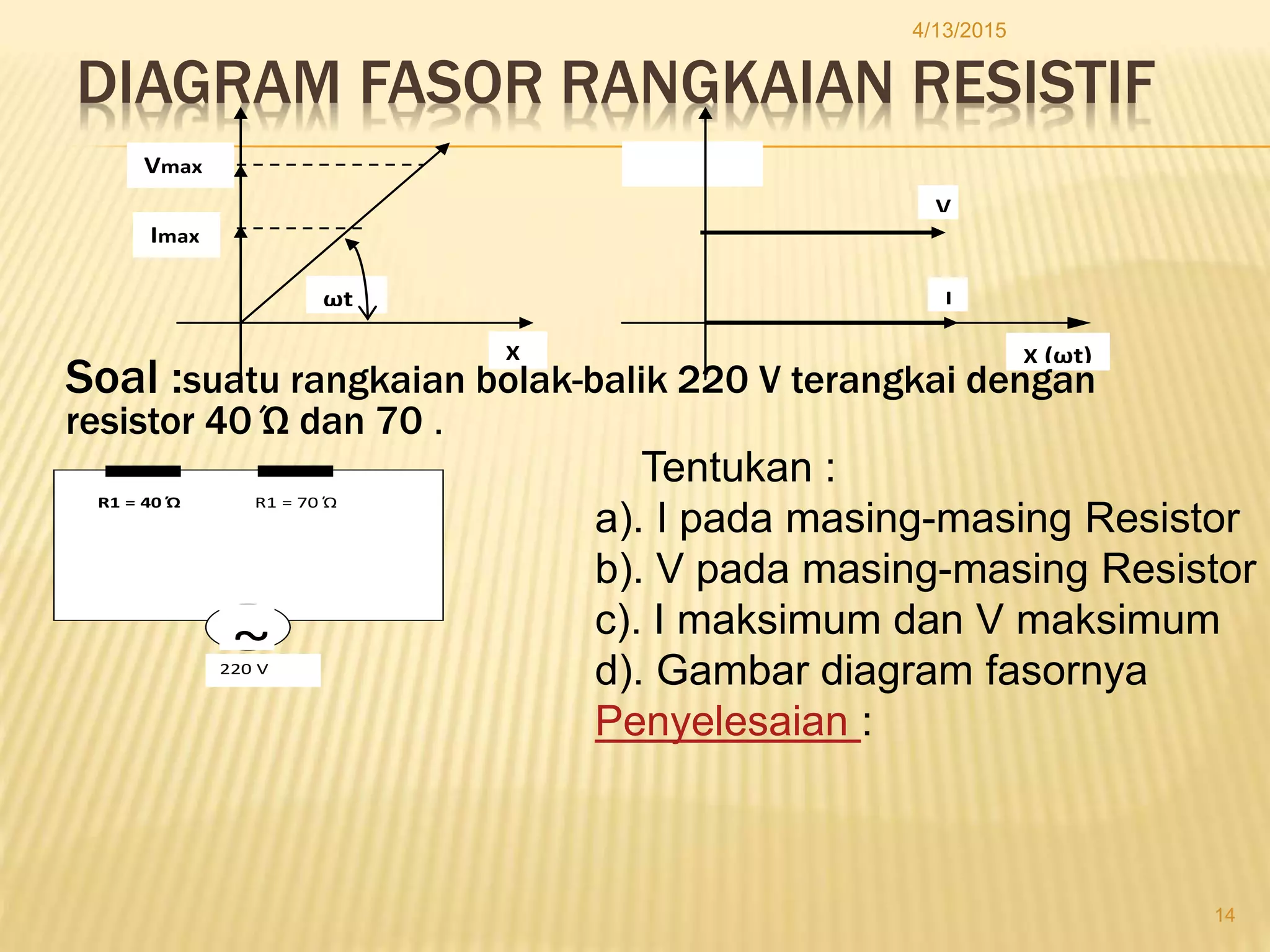
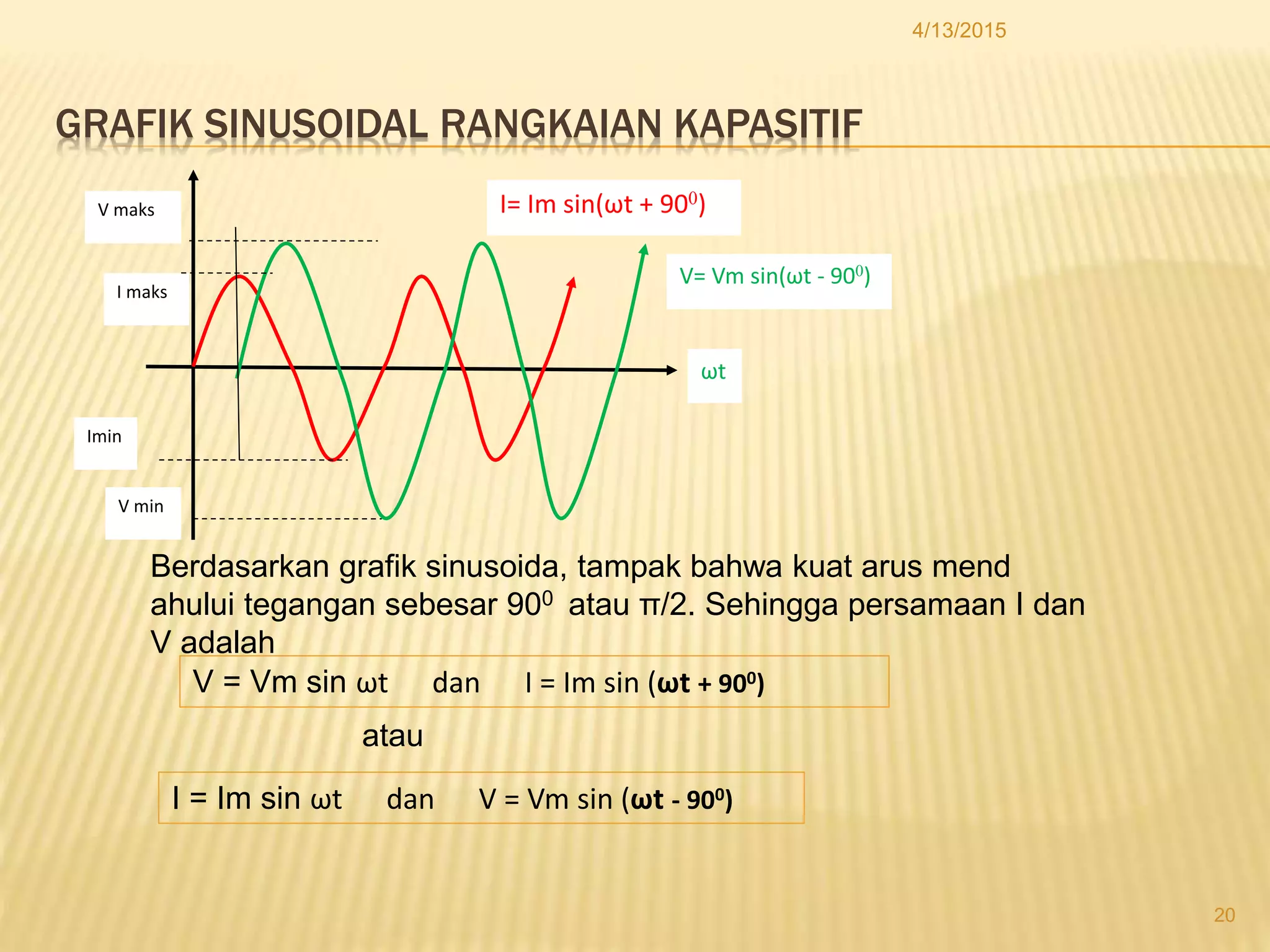
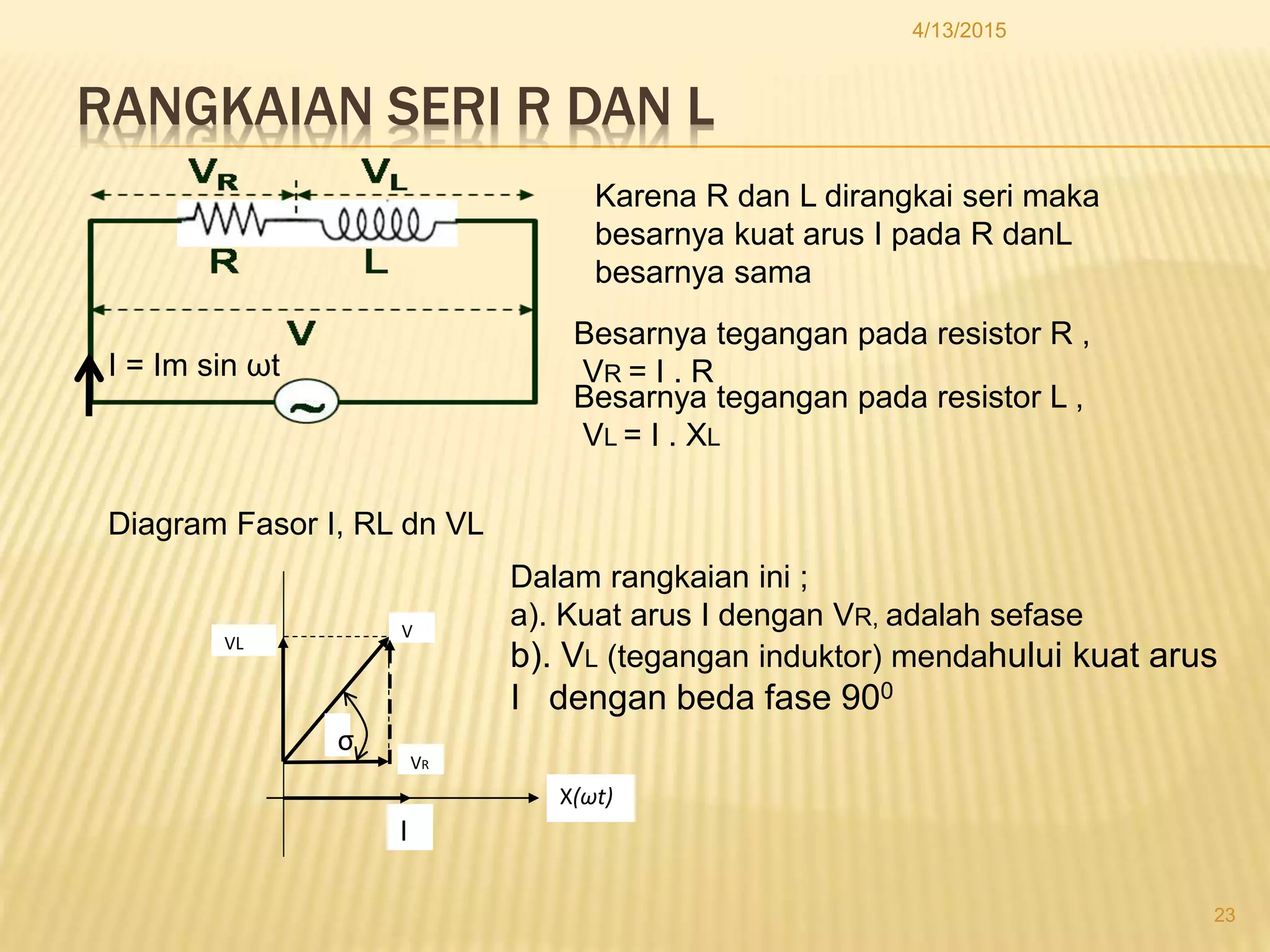
Dokumen tersebut membahas tentang tegangan dan arus bolak-balik (AC), termasuk cara kerja generator AC, grafik sinusoidal arus dan tegangan AC, persamaan arus dan tegangan AC, diagram fasor, dan rangkaian listrik AC seperti rangkaian resistif, induktif, kapasitif, serta kombinasinya.

1. TEGANGAN DAN ARUS BOLAK-BALIK
Tegangan dan arus listrik terdiri atas :
1. Tegangan/arus listrik searah ( DC= Direct Current )
2. Tegangan/arus listrik bolak-balik (AC=Alternating
Current )
4/13/2015
1
Tegangan/arus DC dihasilkan dari baterai
Sedangkan , tegangan/arus AC dihasilkan dari
generator

2. GENERATOR AC
4/13/2015
2

3. CARA KERJA GENERATOR AC
4/13/2015Tegangan dan Arus Bolak-balik
3
Generator AC menghasilkan arus listrik induksi dengan cara memutar kumparan diantara kutub U -
S magnet. Ketika kumparan diputar,terjadi perubahan Flux magnetik didalam kumparan yang
menimbulkan GGL Induksi. Karena Perubahan Flux Magnetik yang masuk dalam kumparan selalu
berubah-ubah sepanjang waktu maka besarnya tegangan juga berubah-ubah sesuai dengan fungsi
waktu.

4. GRAFIK ARUS DC DAN AC
4/13/2015
4

5. 4/13/2015
5

6. ωt
I Min
I Maks
ωt
V Min
VMaks
Persamaan Arus AC
I = I max sin ωt
I = Arus sesaat
I max = arus maksimum
ω = Frekuensi sudut
t = waktu
Persamaan Tegangan AC ;
V = V max sin ωt
V = tegangan sesaat
Vmak = tegangan
maksimum
ωt = sudut fase
4/13/2015
6

7. TEGANGAN DAN ARUS AC DAPAT JUGA DINYATAKAN
DENGAN MENGGUNAKAN DIAGRAM FASOR ( FASE
VEKTOR )
4/13/2015
7
Imax
X(00)
I
ωt
V
ωt
Vmax
X(00)
Jika kita tetapkan sudut fase 00 sebagai acuan sumbu X positif,
sumbu Y merupakan proyeksi Fasor menunjukkan besaran sesaat
dari kuat arus I dan tegangan V.
Sedangkan sudut antara Fasor dan sumbu X positif yaitu ωt
menyatakan sudut fase dari arus dan tegangan

8. CONTOH SOAL
1. Sebuah hambatan 40 ohm dihubungkan dengan suatu sumber tegangan AC
yang mempunyai harga sebagai fungsi waktu yang dinyatakan dengan ; V =
20 SIN 2πt volt.Hitunglah ;
a. Tegangan max
b. Tegangan dari puncak ke puncak
c. Arus listrik maksimum
d. Frekuensi anguler
Penyelesaian :
4/13/2015
8

9. NILAI EFEKTIF ARUS DAN TEGANGAN AC ADALAH NILAI
YANG DIANGGAP SETARA DENGAN TEGANGAN DAN ARUS
SEARAH YANG AKAN MENGHASILKAN JUMLAH KALOR YANG
SAMA KETIKA MELALUI SUATU PENGHANTAR DALAM WAKTU
YANGSAMA.
BESARNYA NILAI EFEKTIF ARUS AC ADALAH
DIMANA : I EFF = KUAT ARUS EFEKTIF, I MAKS = KUAT
ARUS MAKS
V EFF = TEGANGAN EFEKTIF, V MAKS =
TEGANGAN MAKS
IEFF = I UKUR ( I HASIL PENGUKURAN )
VEFF = VUKUR (V HASIL PENGUKURAN)
4/13/2015
9

10. SOAL
Aliran listrik suatu rumah mempunyai
tegangan
220 V,sebuah alat listrik dengan hambatan
50Ω
dipasang pada aliran tersebut,tentukan :
a.Ieff dan Imax
b. Veff dan V max
Penyelesaian :
4/13/2015
10

11. RANGKAIAN ARUS DAN TEGANGAN AC
1. Rangkaian Resistif
Yaitu rangkaian Arus/tegangan AC yang
dihubungkan dengan Resistor
VAB = V = R . I dimana I = Im sin ωt
VAB = V= R ( Im sin ωt )
4/13/2015
11
I = Im sin ωt
A B

12. DIMANA ;
V AB = TEGANGAN ANTAR UJUNG RESISTOR (
VOLT )
VM = TEGANGAN MAKSIMUM
IM = KUAT ARUS MAKSIMUM ( AMPERE )
R = RESISTOR ( OHM )
ΩT = SUDUT FASE ( DERAJAT)
Ω = FREKWENSI SUDUT ( RADIAN/S)
4/13/2015
12

13. GRAFIK RANGKAIAN RESISTIF
4/13/2015
13
Berdasarkan grafik diatas,terlihat tegangan dan
arus pada rangkaian resistif mempunyai fase yang
sama (sefase). Tegangan dan Arus mencapai nilai
maksimum dan minimum pada fase yang sama.
Vmin
Vmax
Imax
Imin
ωt

14. DIAGRAM FASOR RANGKAIAN RESISTIF
ωt
Vmax
Imax
X X (ωt)
V
I
4/13/2015
14
Soal :suatu rangkaian bolak-balik 220 V terangkai dengan
resistor 40 Ώ dan 70 .
~
R1 = 40 Ώ R1 = 70 Ώ
220 V
Tentukan :
a). I pada masing-masing Resistor
b). V pada masing-masing Resistor
c). I maksimum dan V maksimum
d). Gambar diagram fasornya
Penyelesaian :

15. 2. RANGKAIAN INDUKTIF
Yaitu rangkaian tegangan/arus AC yang
dihubungkan dengan lilitan/kumparan(induktor).
4/13/2015
15
~
I = Imax sinωt
L
A B
Besar tegangan antara ujung-
ujung induktor adalah :
Є = VAB = V = L di/dt
Dimana;
Є = GGL induksi
VAB = V = Tegangan AC
L = Induktansi induktor
di/dt = perubahan kuat arus

16. GRAFIK SINUSOIDAL RANGKAIAN INDUKTIF
4/13/2015
16
Vmaks
Imaks
Vmin
V=Vmsinωt
I=Imsinωt
Dari grafik tampak, bahwa tegangan (V)
mendahului I ( Kuat arus ) sebesar 900 atau π/2.
Dengan kata lain;
Kuat arus (I) terlambat sebesar 900 atau π/2
Sehingga persamaan kuat arus dan
tegangannya adalah
V = Vm sin ωt dan I = Im sin (ωt – 900)
atau
I = Im sin ωt dan V = Vm sin (ωt + 900)

17. DIAGRAM FASOR RANGKAIAN INDUKTIF
4/13/2015
17
X
(ωt)
V
I
90
0
Reaktansi Induktif
Yaitu hambatan yang timbul pada
induktor yang dihubungkan dengan
tegangan AC.
Besarnya Reaktansi Induktif dirumuskan :
XL = ω.L Karena, ω= 2πf ,maka XL = 2πf.L
Dimana :
XL= Reaktansi Induktif ( ohm )
ω = Frekuensi sudut (rad/s)
L = Induktansi induktor ( Henry = H)
F = Frekuensi arus ( Hz)

18. CONTOH SOAL :
1. SEBUAH KUMPARAN YANG MEMPUNYAI
INDUKTANSI DIRI 8 HENRY DIPASANG PADA
RANGKAIAN AC YANG BERFREKUENSI 50
HZ.TENTUKAN HAMBATAN INDUKTIFNYA ! JAWAB
2. SEBUAH INDUKTOR DENGAN INDUKTANSI 250
MH,DIHUBUNGKAN DENGAN ARUS BOLAK-BALIK
BERFREKUENSI 50 HZ,JIKA TEGANGAN AC 220
V,TENTUKAN :
A). REAKTANSI INDUKTIF
B). I MAK
C). I EFF
JAWAB :
4/13/2015
18

19. 3. RANGKAIAN KAPASITIF
4/13/2015
19
Yaitu rangkaian tegangan/Arus AC yang
dihubungkan dengan kapasitor
I = Im sin ωt
Besarnya muatan yang
mengalir pada rangkaian
;
Q = C . V = C . Vm sin ωt

20. GRAFIK SINUSOIDAL RANGKAIAN KAPASITIF
4/13/2015
20
V= Vm sin(ωt - 900)
I= Im sin(ωt + 900)
ωt
V maks
I maks
Imin
V min
Berdasarkan grafik sinusoida, tampak bahwa kuat arus mend
ahului tegangan sebesar 900 atau π/2. Sehingga persamaan I dan
V adalah
V = Vm sin ωt dan I = Im sin (ωt + 900)
I = Im sin ωt dan V = Vm sin (ωt - 900)
atau

21. DIAGRAM FASORNYA ADALAH
4/13/2015
21
(ωt)
I
900
V
Reaktansi kapasitif ( XC)
Yaitu hambatan yang timbul pada suatu kapasitas yang dihubungkan ke
rangkaian arus bolak-balik .
XC =
XC =1 /(ωC) Karena, ω = 2πf Maka, XC= 1/ (2πf. C)
Dimana,
XC = reaktansi kapasitif ( ohm )
ω = frekuensi sudut arus ( rad/s)
C = Kapasitas kapasitor ( farad )
F = frekuensi arus AC ( Hertz)
π = 3,14

22. SOAL :
PADA SUATU RANGKAIAN ELEKTRONIKA DIPASANG KAPASITOR
10ΜF.JIKA TEGANGAN KAPASITOR 12 V DAN FREKUENSI KUAT ARUS 50
HZ.TENTUKAN BESARNYA RREAKTANSI KAPASITIF DAN KUAT ARUS YANG
MENGALIR ! JAWAB
4/13/2015
22

23. RANGKAIAN SERI R DAN L
4/13/2015
23
Karena R dan L dirangkai seri maka
besarnya kuat arus I pada R danL
besarnya sama
Besarnya tegangan pada resistor R ,
VR = I . R
Besarnya tegangan pada resistor L ,
VL = I . XL
I = Im sin ωt
Diagram Fasor I, RL dn VL
V
VR
VL
σ
I
X(ωt)
Dalam rangkaian ini ;
a). Kuat arus I dengan VR, adalah sefase
b). VL (tegangan induktor) mendahului kuat arus
I dengan beda fase 900

24. BESARNYA TEGANGAN TOTAL PADA RANGKAIANN SERI L DAN R
4/13/2015
24
Vtotal
 Besarnya sudut fase (σ) antara I dan V
tgσ = VL/ VR = (I.XL) / ( I. R) = XL / R
 Besar hambatan total pada rangkaian di sebut Impedansi
22
LXRZ  Z = Impedansi ( ohm)
R = resistor ( ohm )
XL = reaktansi induktor ( ohm)

25.  BESAR KUAT ARUS PADA RANGKAIAN
4/13/2015
25
22
LXR
V
Z
V
i



26. 5. RANGKAIAN SERI R DAN C
4/13/2015
26
R C
I = Im sin ωt
 Kuat arus yang mengalir pada
rangkaian seri R dan C sama besar.
 Besar tegangan pada resistor,
VR = I. R
 Besar tegangan pada kapasitor,
VC = I. XC
X (ωt)
σ
I
V
VR
VC
Diagram Fasor I, VR dan VC
 Besar tegangan antara ujung-ujung rangkaian seri R-C
22
CR VVV 
 Besar sudut fase antara I ,VR dan VC
Tg σ = - VC = - = -
Sehingga, σ = arc Tg – ()

27. 4/13/2015
27
6. RANGKAIAN SERI INDUKTOR (L) DAN KAPASITOR(C)
 Kuat arus yang mengalir pada rangkaian sama
IL = IC
 Besar tegangan pada masing-masing komponen
VL = I. XL
VC = I . XC
VL = Vm sin ( ωt + 900 )
VC = Vm sin (ωt - 900 )
Diagram fasor pada rangkaian seri L-C
VL
VC
I
X (ωt)
V
VL > VC
VL
VC
I
X (ωt)V
VL < VC
VL
VC
I
X (ωt)
V=0
VL = VC

28. 4/13/2015
28
 Karena pada rangkaian seri L dan C,maka arus I yang mengalir sama besar.
IL = IC = I
 VL mendahului arus I sebesar 900 , maka fasor VL digambarkan pada sumbu tegak
positif
 Vc tertinggal dari arus I sebesar 900 , maka fasor Vc digambarkan pada
sumbu tegak negatif
Untuk menghitung tegangan total VAB atau V pada rangkaian seri L dan C ini
dapat dijumlahkan secara aljabar karena VL dan VC berbeda fase tepat 1800
 V = VL – VC jika VL > VC , dimana = 900 rangkaian bersifat induktif
 V = VC – VL jika VL < VC, dimana = -900 rangkaian bersifat kapasitif
 V = 0 jika VL = VC , dimana = 00 terjadi peristiwa resonansi

29. IMPEDANSI RANGKAIAN L-C
4/13/2015
29
1). Jika XL > XC , maka Z = XL – XC
2). Jika XC > XL , maka Z = XC – XL
3). Jika XL = XC , maka Z = 0 (nol)
Resonansi pada rangkian L – C
Resonansi pada rangkaian L-C terjadi pada saat XL = XC,
XL = XC
C
L
XX CL


1



30. 7. RANGKAIAN SERI R-L-C
4/13/2015
30
Besar kuat arus yang melalui R,L,C
adalah sama besar,
sehingga IR=IL=IC
Besar tegangan pada masing-masing
komponen ;
VR = I. R
VL = I. XL
VC = I. XC
Menentukan sudut fase antara arus dan tegangan
jika arus listrik, I = Im sin ωt , maka
VR= Vm sin ωt
VL = Vm sin ( ωt + 900)
Vc = Vm sin ( ωt – 900 )

31. DIAGRAM FASOR
4/13/2015
31
Dari diagram fasor,diperoleh ;
1). VR sefase dengan I
2). VL mendahului I sebesar 900
3). VC terlambat terhadap arus I sebesar 900
VL
V
VR
VC
(VL-VC)
θ
X(ωt)
I
Untuk menghitung tegangan total VAB atau V pada rangkaian RLC dapat
dijumlahkan secara aljabar.Karena VL dan VC berbeda fase tepat 1800
(berlawanan arah ).
22
)( CLR VVVV 

32. ) BESAR SUDUT FASE (Θ)
4/13/2015
32
atau Θ = arc Tg (XL – XC)
R
). Besar hambatan total pada rangkaian
disebut juga Impedansi ( Z)
22
)( CL XXRZ 
Z
XL - XC
R
θ
). Besar kuat arus total
I total = Vtotal
Z

33. ) RESONANSI PADA RANGKAIAN SERI RLC
4/13/2015
33
a). Jika XL > XC, Tg θ = (Xl – XC ) =bernilai positif
R
sudut fase (θ) bernilai positif, maka rangkaian bersifat INDUKTIF
b). Jika XL < XC, Tg θ = (Xl – XC ) =bernilai negatif
R
sudut fase (θ) bernilai negatif, maka rangkaian bersifat KAPASITIF
C). Jika XL = XC, Tg θ = (Xl – XC ) =bernilai 0 (Nol)
R
Impedansi rangkaian Z bernilai sama dengan R. Pada kondisi ini
tegangan V sefase kuat arus I dan rangkaian bersifat RESISTIF.
*). Peristiwa ketika XL =XC, rangkaian bersifat resistif disebut dengan
peristiwa RESONANSI

34. . FREKUENSI SUDUT RESONANSI DAN FREKUENSI RESONANSI
4/13/2015
34
Resonansi pada rangkaian seri RLC terjadi pada saat XL = XC
Dari hubungan ini kita menghitung besarnya sudut Resonansi (ωr) dan
frekuensi resonansi (Fr)
Dari persamaan
Sehingga, ωr2 = 1
LC
Dengan mensubstitusikan
C
L
XX CL


1


ωr = 2 πfr
ωr = frekuensi sudut resonansi(rad/s)
L = induktansi induktor (H)
C = kapasitas kapasitor ( F)
Fo = fr= Frekuensi resonansi ( Hz)
Π = 3,14

35. ). DAYA PADA RANGKAIAN BOLAK-BALIK
4/13/2015
35
P = Vef. Ieff atau P = (Ieff)2. R
Jika sudut fasenya θ, maka ;
P = Veff . Ieff cos θ atau P = Ieff2 . Z cos θ
Dimana ;
P = daya rata-rata arus AC ( watt)
Veff = tegangan efektif ( volt)
Ieff = Kuat arus efektif ( ampere)
Θ = sudut fase ( rad/s)
Cos θ = faktor daya
). Faktor daya ( Cosθ )
dari persamaan P = Ieff2. Z cos θ
Cos θ = P / Ieff2. Z karena P = (Ieff)2. R
Cos θ = R / Z
Atau Cos θ = VR / Vmax