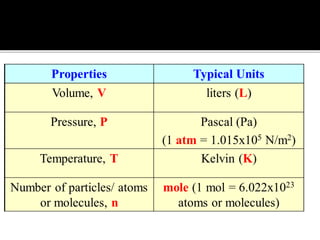
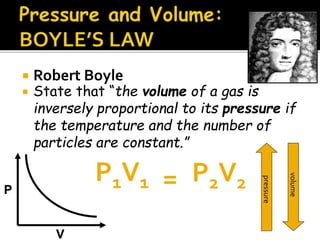
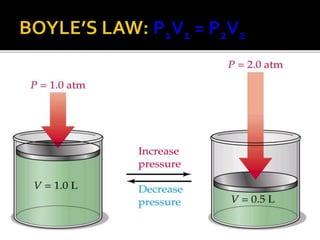
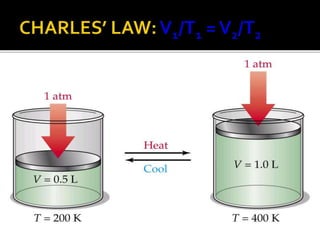
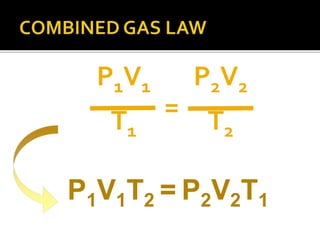
The document outlines key concepts related to gas behavior, including Boyle's Law, Charles's Law, and Gay-Lussac's Law, along with the ideal gas equation. It explains how gases behave under various conditions of pressure, volume, and temperature, and includes problem-solving examples to illustrate these laws. Additionally, it discusses Avogadro's principle regarding the relationship between gas volume and the number of moles at constant temperature and pressure.

1. Grade 10: Fourth Quarter

2.  Module 1: Behavior of
Gases
 Boyle’s Law
 Charles’ Law
 Gay-Lussac’s Law
 Combined Gas Laws
 Module 2: Chemical
Reactions
 Chemical change
 Chemical equation
 Types of chemical reactions
 Law of conservation of mass
 Factors affecting reaction
rate
 Module 3: Biomolecules
 Carbohydrates
 Lipid
 Proteins
 Nucleic acids

3. Have you ever:
Seen a hot air balloon?
Had a soda bottle spray all over you?
Baked (or eaten) a nice, fluffy cake?
These are all examples of gases at work!

4.  Gases have different properties.
 Indefinite shape and size
 Fit the shape and size of their containers.
 Far from one another
 Highly compressible
 Able to flow
 Have mass, volume, temperature, and
pressure.

5. Pressure
Volume
Number of particles
Temperature

6.  It is the force applied by the gas
particles per unit area.
P =
𝐹
𝑎
Where: P = Pressure
F = Force
a = area

7. Lower pressure Higher pressure
Collisions between particles of a gas and
the walls of the container cause the
pressure in a closed container of gas.

8.  N/m² or pascal (Pa)
 One pascal is a small amount of pressure.
 One Kilopascal (kPa) = 1000 Pa
 At sea level, average atmospheric pressure is
about 101 kPa. Scientists used this value as a
basis to define one standard atmosphere (1
atm), or standard pressure, as exactly 101.325
kPa.
 Pressure units and their equivalents:
 1 atm = 760 mm Hg = 76 cm Hg = 760 torr =
101325 Pa = 14.6956 psi(pounds per square inch)

9.  Factors that affect the
pressure of an enclosed gas are:
 Its temperature
 Its volume
 The number of its particles

10.  Increasing the number of particles will
increase the pressure of a gas if the
temperature and the volume are
constant.

11.  It is the measure of the coldness or hotness
of the gas.
 Raising the temperature of a gas increases
the pressure, if the volume and number of
particles are constant.
 Always use absolute temperature (Kelvin)
when working with gases.
ºF
ºC
K
-459 32 212
-273 0 100
0 273 373

12.  It is the amount of space occupied by the
gases.
 It is the three-dimensional space inside
the container holding the gas.
 Reducing the volume of a gas increases its
pressure if the temperature of the gas
and the number of particles are constant.
 The SI unit for volume is the cubic meter,
m3. A more common and convenient unit is
the liter, L.

14. The observable properties of the gases are explained by the different gas
laws.

15.  Robert Boyle
 State that “the volume of a gas is
inversely proportional to its pressure if
the temperature and the number of
particles are constant.”
P
V
P1V1 = P2V2
pressure
volume

17.  A balloon contains 30.0 L of helium
gas at 103 kPa. What is the volume
of the helium when the balloon
rises to an altitude where the
pressure is only 25.0 kPa. (assume
that the Temperature remains
constant)

18.  Jacques Charles
 state that “the volume of a gas is
directly proportional to its temperature
if the pressure and the number of
particles of the gas are constant.”
volume
temperature
V
T

20.  Gas law problems involving temp. will
always require that the temp. be in
Kelvin (K).
 K = °C + 273
 °C = K - 273

21.  A balloon inflated in a room at
24°C has a volume of 4.oo L.
The balloon is then heated to a
temperature of 58°C . What is
the new volume if the
pressure remains constant?

22.  The relationships described by Boyle’s law
and Charles’s law can be described by a single
law.
 Describes the relationship among the
Temperature, volume and pressure of a gas
when the number of particles is constant.

23. P1V1
T1
=
P2V2
T2
P1V1T2 = P2V2T1

24. A cylinder that contains air at a
pressure of 100 kPa and has a volume
of 0.75 L at 0°C. The pressure is
increased to 300 kPa at 25°C. Find
the new volume.

25.  Joseph Louis Gay-Lussac
 states that “the pressure of a given amount
of gas held at constant volume is directly
proportional to the temperature.”
P
T
P1
T1
=
P2
T2
pressure
temperature

26.  A sealed storage tank contains
argon gas at 18°C and a
pressure of 825 kPa at night.
What is the new pressure if the
tank and its contents warm to
32°C during the day?

27. Solve the following problems.

28. 1. A gas has a volume of 5.0 L at a pressure of 50
kPa. What happens to the volume when the
pressure is increased to 125 kPa? The temp. does
not change.
2. An oxygen tank contains 550 L oxygen at 28°C.
What will be the final volume if the temperature
is increased to 32°C assuming that pressure was
fixed at 1.00 atm?
3. What is the volume of methane at 0°C and 760
torrs, if its original volume at 25°C and 746 torrs
is 23.9 cm³?
4. A sample of Neon gas in a gas cylinder has a
pressure of 125 kPa at 300 K. The cylinder is
slowly heated. Predict the pressure at 400 K.

29.  Amedeo Avogadro
 “Equal volumes of all gases, kept at the
same pressure and temperature, contain
the same number of molecules.”
 Avogadro was the first to suggest that
the volume of a gas is directly
proportional to the number of moles of
gas present at a given temperature and
pressure.

30.  Equal volumes of gases contain equal numbers of
moles
 at constant temp & pressure
 true for any ideal gas
V
n
V1
n1
=
V2
n2
volume
#ofmoles

31.  What will be the final volume of a
5.00 LHe gas which contains 0.965
mole of at 30°C and 1.00
atmosphere, if the amount of this
gas is increased to 1.80 moles
provided that temperature and
pressure remains unchanged?

32.  The ideal gas equation replaces the simple gas
laws with a single equation that includes the
four gas variables/properties – volume,
pressure, temperature and number of particles.
P V = n R T
Where: P = Pressure n = no. of moles
V = Volume R = gas constant
T = Temperature
*1 mol gas = 22.414 L gas at STP

33. P V = n R T
P = 1.00 atm
V = 22.414 L
n = 1 mol
T = 273 K
R = 0.082058 L atm/mol K or 0.0821 L
atm mol ¹K ¹

34.  How many moles of helium gas
are in 5.0 L storage tank filled
with this gas at 10.5 atm
pressure and at 30ºC?

37. 1. Imagine that a gas is inside a cylinder with a
movable piston. If the volume of a gas is 2.0
L when the pressure is 760 torrs; what is the
volume of the gas if the pressure is halved?