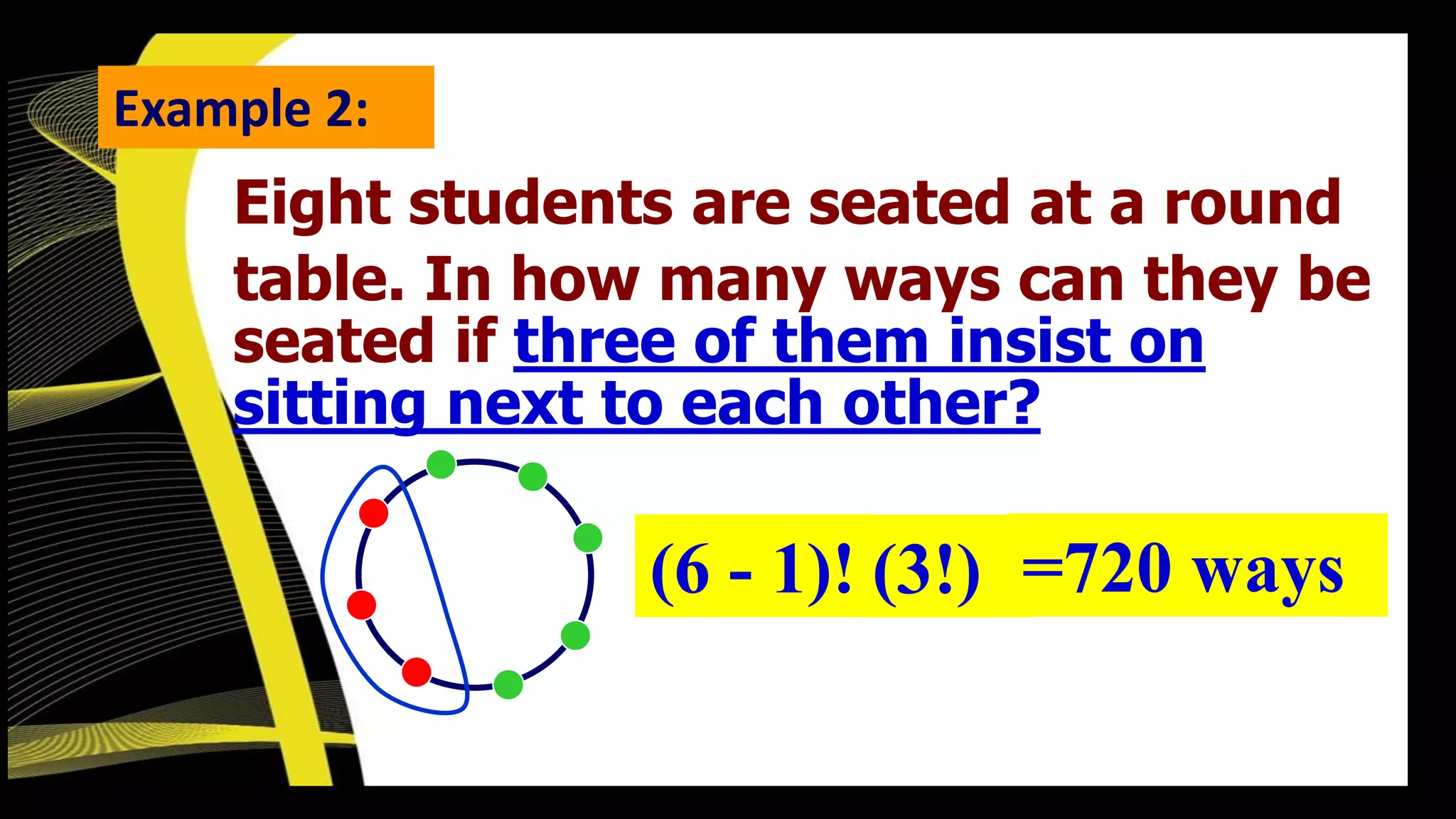
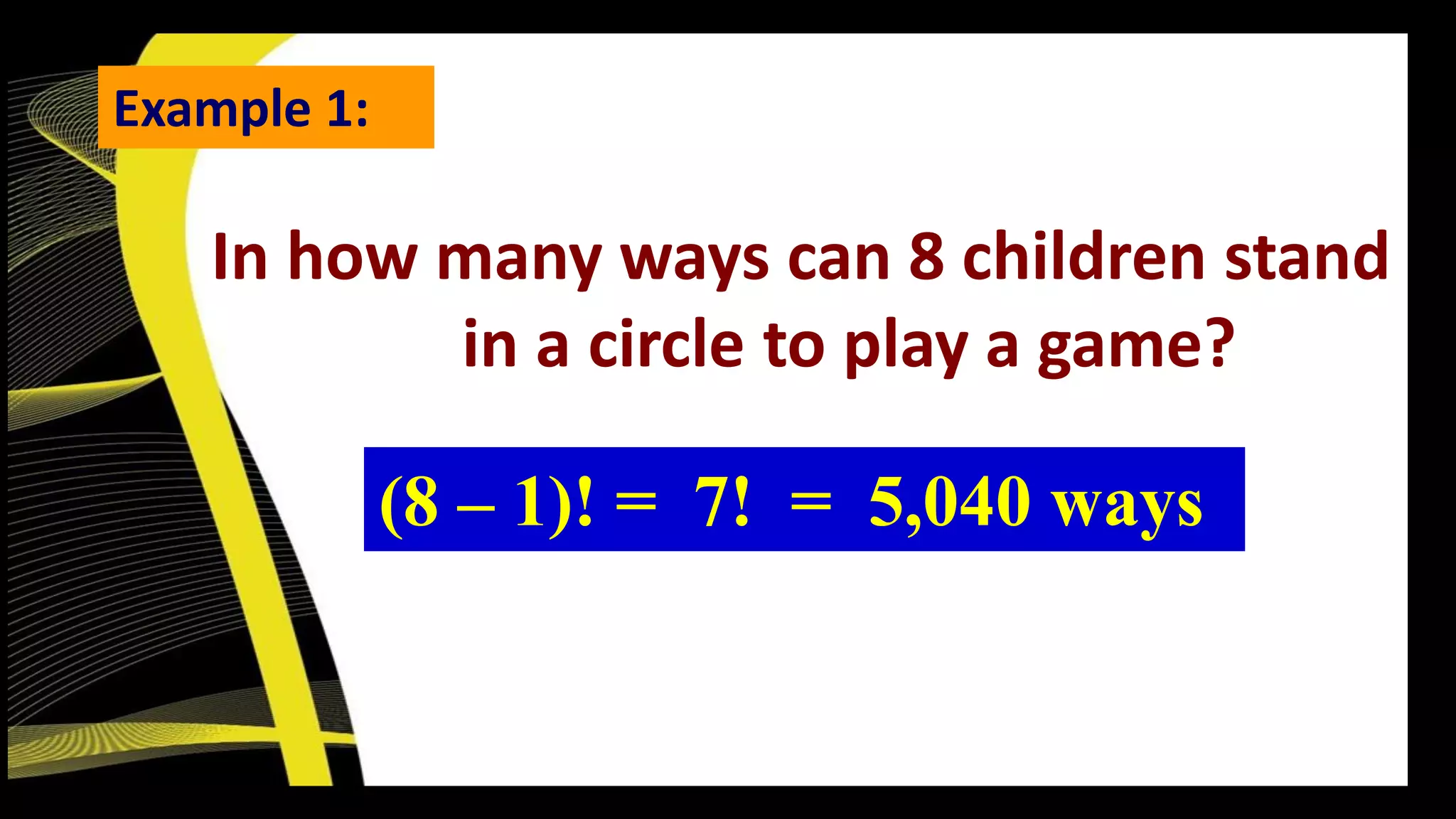The document is a mathematics lesson prepared by Loreto A. Elardo Jr., covering various combinatorial problems involving permutations and arrangements. It includes examples of problems related to seating arrangements, licensing plate combinations, and the arrangement of books, detailing calculations and principles like permutations and circular arrangements. The document emphasizes the importance of order in permutations and provides solutions for specific scenarios involving restrictions on arrangements.

1. Prepared by:
LORETO A. ELARDO JR.
Math 10 Teacher

3. AJ bag factory manufactures ladies bags
in 8 styles, 6 colors and 4 sizes.
How many different bags are available?
x x =8 6 4 192

4. A car license plate consists of any three
letters followed by any three digits.
How many possible license plates are
there?
P Y P 2 8 8
MATATAG NA REPUBLIKA
-
2012
26 26 26 10 10 10x x x x x = 17,576,000

5. A car license plate consists of any three
letters followed by any three digits.
How many possible license plates are
there if there are no repetition of letters
and digits?
26 25 24 10 9 8x x x x x = 11,232,000

6. A witness to a hit-and-run accident told the
police that the plate number of the suspect’s car
contained the letters X L followed by a different
letter, and then followed by three digits, the first
of which is 4. The witness cannot recall the last 2
digits, but is certain that all 3 digits are different.
Find the maximum number of car registrations
that the police may have to check.
1 1 24 1 9 8x x x x x = 1,728

7. How many 11-digit cellphone
numbers can be formed if each
begins with 0917?
0917- 10 10 10 10 10 10 10x x x x x x
10,000,000

8. If there are 5 roads from Town A to
Town B, 3 roads from Town B to
Town C, and 2 roads from Town C
to Town D. In how many ways can
one go from Town A to Town D and
back to Town A, through B and C,
without passing through the same
road twice?

9.  Which situations is order or
arrangement of the selection
important?
 Justify your answer by giving examples.

10. PERMUTATION refers to the different
possible arrangement of objects.

11. The number of permutations of n objects
taken r at a time is;
𝑷 𝒏, 𝒓 =
𝒏!
𝒏 − 𝒓 !
, 𝒏 ≥ 𝒓

12. A permutation is an arrangement
of n objects with no repetitions
and the order is important.
Permutations of n distinct objects taken r at a
time where r < n : P(n,r)

13. 1. General Permutation
2. Distinguishable Permutation
3. Circular Permutation

14. Given the 4-letter word READ. In
how many ways can we arrange
the letters 3 at a time?
Use,
𝑷 𝒏, 𝒓 =
𝒏!
𝒏 − 𝒓 !

15. Problem 1: In how many ways can 6
children be seated in a row of 6
chairs?
𝑷 𝟔, 𝟔 =
𝟔!
𝟔−𝟔 !
=
𝟔!
𝟎!
=
𝟔 𝟓 𝟒 𝟑 𝟐 𝟏
𝟏
= 𝟕𝟐𝟎 𝒘𝒂𝒚𝒔

16. Factorial Notation
n! = n(n-1)(n-2)(n-3) . . . (2)(1)
0! = 1
3! = (3)(2)(1) = 6
4! = (4)(3)(2)(1) = 24

17. Problem 2. In how many ways can 10
children be seated in a row of 6 chairs?
n = 10 , r = 6
10 6
10!
P
(10 6)!


10!
4!

10(9)(8)(7)(6)(5)(4!)
4!

= 151,200 ways

18. Problem 3: A photographer is taking a group
picture of 5 people in a row . In how many ways
can this be done if
a. There are no restrictions.
P(5,5)= (5)(4)(3)(2)(1) =
120 ways
n=5; r =5

19. b. Mel and Vic insist on standing next to
each other.
Consider Mel and Vic as one object. So, we have 4
objects to arrange in a row and there are
P(4,4)=120 ways
For each of these arrangements, there are two
ways to arrange Mel and Vic : Mel-Vic or Vic-
Mel
Therefore, 𝟐 𝑷 𝟒, 𝟒 = 𝟐 𝟒! = 𝟐 𝟐𝟒 =
𝟒𝟖 𝒘𝒂𝒚𝒔

20. c. Mel and Vic refuse to stand next to each
other.
There are 5! ways to arrange the 5 people. Of these
120 ways, Mel and Vic stand together in 2(P(4,4))
ways.
5! – 2 (P(4,4)) = 120 - 48 = 72 ways
Therefore, in all the remaining, Mel and Vic stand
apart.

21. In how many ways can 4 math books
and 5 science books be arranged on
a shelf if
a. there are no restrictions.
= 362,880 waysP(9,9)= 9!
n=9; r=9

22. In how many ways can 4 math books
and 5 science books be arranged on
a shelf if
b. the 4 math books are together.
= 720 (24) = 17,2806! 4!

23. In how many ways can 4 math books
and 5 science books be arranged on
a shelf if
c. books of the same subject are together.
4 MATH
BOOKS
5 SCIENCE
BOOKS
4! ways 5! ways
5 SCIENCE
BOOKS
4 MATH
BOOKS
or
5! ways 4! ways
Total no. of ways = 2 (4! 5!) = 2 (24)(120) = 5,760

24. Find the number of permutations of
the letters of the word STATISTICS.
Use,
𝑷 =
𝒏!
𝒑! 𝒓! 𝒔! …

25. an arrangement of objects in a circular manner.
B
C
A C
A
BA
B
C
(same as) (same as)
C
B
A A
C
B B
A
C
(same as) (same as)
Fix A and permute B and C. So, we have only two arrangements.

26. In a circular permutation, consider
one object first in a fixed
position and arrange the
remaining (n-1) objects in the
remaining (n-1) positions.
The number of permutations of n
distinct objects arranged in a circle is
(n – 1)!

27. (8 – 1)! = 7! = 5,040 ways
Example 1:
In how many ways can 8 children stand
in a circle to play a game?

28. Example 2:
Eight students are seated at a round
table. In how many ways can they be
seated if three of them insist on
sitting next to each other?
(6 - 1)! (3!) =720 ways

29. Example 3:
(7 - 1)! (2!) =6!2!
In how many ways can 8 persons be seated
on a round table if two of them want to
be together?
=(720)(2)
=1,440 ways

30. Example 3:
(8 - 1)! -6!2! =7!-6!2!
In how many ways can 8 persons be seated
on a round table if two of them refuse
to be together?
=5,040-1,440
=3,600 ways

31. 1. 𝑷 𝟔, 𝟔
2. 𝑷 𝟏𝟎, 𝟓
3. 𝑷 𝟖, 𝟑
4. 𝑷 𝟕, 𝟒
5. 𝑷 𝟗, 𝟖

32. There are 4 different Mathematics
books and 5 different Science books. In
how many ways can the books be
arranged on a shelf if
1. There are no restrictions?
2. Books of the same subject must be
placed together?
3. If they must be placed alternately?

33. Five couples want to have their
pictures taken. In how many
ways can they arrange
themselves in a row if
1. Couples must stay together?
2. They may stand anywhere?

34. There are 12 people in a dinner
gathering. In how many ways can a host
(one of the 12) arrange his guests
around a dining table if
1. They can sit on any of the chairs?
2. 3 people insist on sitting beside each
other?
3. 2 people refuse to sit beside each
other?