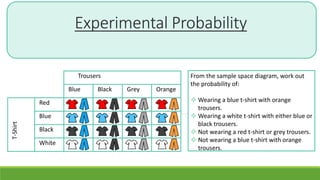
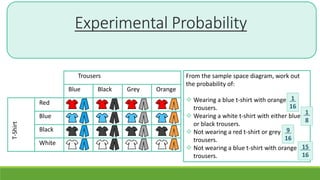
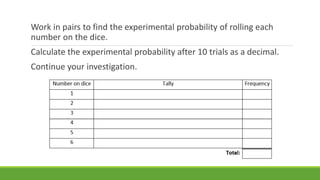
The document discusses experimental probability and how it is calculated by performing trials of an experiment and recording the number of successful outcomes. It provides examples of calculating experimental probability based on rolling dice and cars moving in a race based on dice rolls. The document aims to help students understand what experimental probability means, become familiar with experimenting with chance, and compare experimental and actual probability.

1. HOOK
Sometimes it is not straightforward to work out the probability of an event. For
example the probability of there being a rainbow tomorrow, a product being
faulty or your toast landing butter side up if you drop it.
How would we find the probability of these events?

2. LEARNING INTENTION/GOALS
TO UNDERSTAND WHAT EXPERIMENTAL PROBABILITY MEANS
TO BECOME FAMILIAR WITH EXPERIMENTING WITH CHANCE
TO COMPARE EXPERIMENTAL AND ACTUAL PROBABILITY
SUCCESS CRITERIA
I UNDERSTAND WHAT EXPERIMENTAL PROBABILITY MEANS
I AM FAMILIAR WITH EXPERIMENTING WITH CHANCE
I CAN COMPARE EXPERIMENTAL AND ACTUAL PROBABILITY

3. Explicit Vocabulary
A trial is one performance of an experiment
An experiment is a process allowing collections of information by performing trials
A successful trial is one that results in the desired outcome
The Experimental probability of an event is found by calculating an experiment and counting the number of times the
event occurs and it is defined as:
pr (event) = Number of successful trials
Number of possible outcomes

4. Experimental Probability
Trousers
Blue Black Grey Orange
T-Shirt
Red
Blue
Black
White
From the sample space diagram, work out
the probability of:
 Wearing a blue t-shirt with orange
trousers.
 Wearing a white t-shirt with either blue or
black trousers.
 Not wearing a red t-shirt or grey trousers.
 Not wearing a blue t-shirt with orange
trousers.

5. Experimental Probability
Trousers
Blue Black Grey Orange
T-Shirt
Red
Blue
Black
White
From the sample space diagram, work out
the probability of:
 Wearing a blue t-shirt with orange
trousers.
 Wearing a white t-shirt with either blue
or black trousers.
 Not wearing a red t-shirt or grey
trousers.
 Not wearing a blue t-shirt with orange
trousers.
1
16
1
8
9
16
15
16

6. Experimental Probability = Number of Favourable Outcomes
Total Number of Trials
5 heads, 5 tails
Experimental Probability
P(H) = = 0.66
10
P(T) = = 0.44
10
Does this mean the coin is unfair?
If I flip a coin 10 times how many heads and how many tails would I
expect to see?

7. Experimental Probability
I have made some dice. It is your job to decide as a class whether the dice are
fair or not.

8. Work in pairs to find the experimental probability of rolling each
number on the dice.
Calculate the experimental probability after 10 trials as a decimal.
Continue your investigation.

9. Car race
12 cars are having a race.
To move the cars roll two dice, find the total score and move that car
forward 1 space.
Calculate the experimental probability of each car winning.
1 2 3 4 5 6 7 8 9 10 11 12

10. Car race
Which car won the most races?
Which car didn’t win any races?
Why are some cars more likely to win than others?
Complete a sample space diagram for rolling 2 dice. Work out
the theoretical probability of getting each number, how do your
experimental results compare.

11. Car Race
Look at all the possible combinations when rolling two dice:
2 3
3
4
4
4
5
5
5
5
6
6
6
6
6
7
7
7
7
7
7
8
8
8
8
8
9
9
9
9
10
10
10
11
11
12

12. Review
My understanding of experimental probability is ……………………………………….