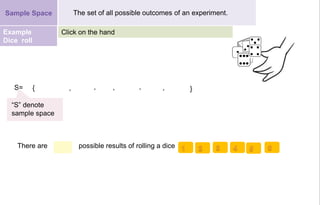
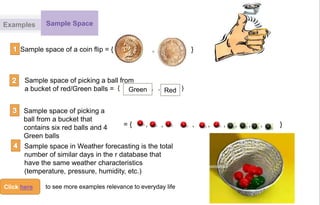
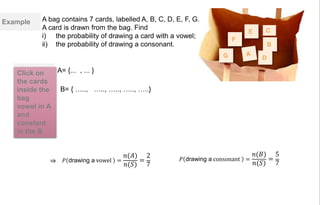
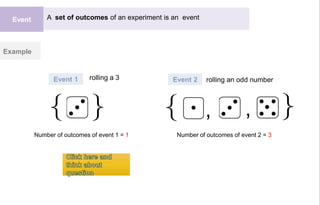
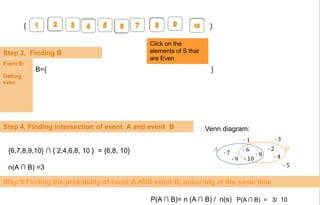
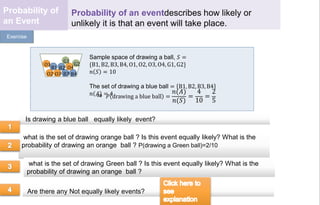
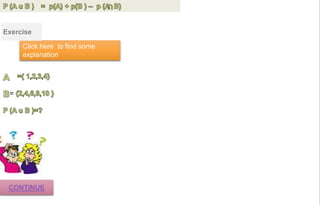
The document discusses key concepts in probability theory including: (i) Defining a sample space as the set of all possible outcomes of an experiment. (ii) Determining the number of outcomes of an event, which is a subset of the sample space. (iii) Calculating the probability of an event as the number of outcomes in the event divided by the total number of outcomes in the sample space. (iv) Calculating probabilities of two events occurring together (using intersections) or either occurring (using unions) based on the number of outcomes in the events and their relationships.

1. (i) describe the sample space of an experiment.
(ii) determine the number of outcomes of an event.
(iii) determine the probability of an event.
(iv) determine the probability of two events:
a) 𝐴 or 𝐵 occurring,
b) 𝐴 and 𝐵 occurring.

2. See the video then click on the
words that highlighted
Experiment sample space
Event, Probability of an event ,
probability of two events,
Summary
Play a game
Probability theory is the branch of mathematics concerned with probability.

3. You must have used a dice when playing board games like monopoly.
Dice rolling is an example of an experiment.
In probability theory, an experiment or trial is any procedure that can be infinitely repeated
and has a well-defined set of possible outcomes, known as the sample space
.
CONTINUE

4. There are possible results of rolling a dice
Click on the handExample
Dice roll
{ }S= , , ,, ,
“S” denote
sample space
Sample Space The set of all possible outcomes of an experiment.

5. Examples
Sample space of a coin flip = { , }
Sample space of picking a
ball from a bucket that
contains six red balls and 4
Green balls
= { , , , , , , , , , }
Sample space of picking a ball from
a bucket of red/Green balls = { , , }Green Red
Sample Space
Sample space in Weather forecasting is the total
number of similar days in the r database that
have the same weather characteristics
(temperature, pressure, humidity, etc.)
Click here to see more examples relevance to everyday life

6. { } { }, ,
Event 1 Event 2
Event
Example
Number of outcomes of event 1 = 1 Number of outcomes of event 2 = 3
rolling an odd numberrolling a 3
A set of outcomes of an experiment is an event

7. A bucket contains two green balls, four orange balls and
four blue balls.
A ball is drawn randomly from the bucket.
Is drawing a blue ball from the bucket an
event?
Exercise

8. Sample space of
drawing a ball =
{B1, B2, B3, B4, O1, O2, O3, O4, G1, G2}
The set of drawing a
blue ball =
{B1, B2, B3, B4}
This is a subset of
the sample space,
B1B2
B3B4
O1
O2O3
G1G2
Explanation:
Your answer is not correct,
Please see explanation
about event. Then click on
the continue, come back
and answer the question
CONTINUE

9. Ok ! That is correct
CONTINUE
Sample space of drawing a ball =
{B1, B2, B3, B4, O1, O2, O3, O4, G1, G2}
The set of drawing a blue ball =
{B1, B2, B3, B4}
This is a subset of the sample space,
so it is an event of the experiment.
B1 B2
B3 B4
O1
O2 O3
G1
G2
Explanation:

10. Sample space of drawing a ball, 𝑆 =
{B1, B2, B3, B4, O1, O2, O3, O4, G1, G2}
𝑛 𝑆 = 10
The set of drawing a blue ball = B1, B2, B3, B4
𝑛 𝐴 = 4𝑃 drawing a blue ball =
𝑛(𝐴)
𝑛(𝑆)
=
4
10
=
2
5
⇒
B1 B2
B3 B4
O1
O2 O3
O4
G1
G2
Exercise
what is the set of drawing orange ball ? Is this event equally likely? What is the
probability of drawing an orange ball ? P(drawing a Green ball)=2/10
what is the set of drawing Green ball ? Is this event equally likely? What is the
probability of drawing an orange ball ?
Is drawing a blue ball equally likely event?
Probability of
an Event
Probability of an eventdescribes how likely or
unlikely it is that an event will take place.
Are there any Not equally likely events?

11. Solution
Example
When you roll a fair dice, calculate the probability of rolling an odd
number.
If the dice is not fair the probability of rolling an odd number would be equally likely event?

12. Example
Solution
Let the sample space of drawing any card be 𝑆, so
𝑛 𝑆 = 7
Let the event of drawing a card with a vowel be 𝐴, so
𝑛 𝐴 = 2
𝑃 drawing a vowel =
𝑛(𝐴)
𝑛(𝑆)
=
2
7⇒
A bag contains seven cards, labelled A, B, C, D, E, F, G.
A card is drawn from the bag. Find the probability of drawing a card
with a vowel.

13. how likely is it to draw a blue ball
from a bucket of red/blue balls?
how likely is it to draw a blue ball
from a bucket that contains4 red
balls and 4 blue balls ?

14. Example Each numeral on a fair die is equally likely to
occur when the die is tossed. Sample space of
throwing a die: { 1, 2, 3, 4, 5, 6 }
Click on the
video and see
explanation
about
equally likely
events
Equally
likely events

15. the video
shows
explanation
about Not
equally likely
events
Events that are Not Equally-Likely
Click on the
explanation and
See about NOT
equally likely
events
Explanation

16. classical
probability
The classical theory of probability applies to "Equally likely events “,
the events that were known as "equipossible".

17. B) Relative Frequency Probability (Experimental Probability)
𝑃 𝐴 =
number of outcomes that belongs to event A
total number of observed outcomes
Repeat the experiment many times and observe the outcomes. Probability can be estimated by
using the following formula:
C) Subjective Probability
An educated guess at how likely is an event, based on knowledge and experience.
It is commonly used in
- the sale of insurance policies such as car insurance, medical insurance etc.
- weather forecast
- determining the success rate of products by managers
In this module we will only use classical probability.!

18. Example
Click on
the cards
inside the
bag
vowel in A
and
constant
in the B
𝑃 drawing a vowel =
𝑛(𝐴)
𝑛(𝑆)
=
2
7⇒
A bag contains 7 cards, labelled A, B, C, D, E, F, G.
A card is drawn from the bag. Find
i) the probability of drawing a card with a vowel;
ii) the probability of drawing a consonant.
𝑃 drawing a consonant =
𝑛(𝐵)
𝑛(𝑆)
=
5
7
B
D
E
F
G
A= {... , ... }
B= { ….., ….., ….., ….., …..}
C

19. Example
Solution
a) Let 𝐴 be the event of obtaining two heads, 𝑛 𝐴 = 1. So,
b) Let 𝐵 be the event of obtaining one head and one tail, 𝑛 𝐵 = 2. So,
𝑃 𝐵 =
𝑛(𝐴)
𝑛(𝑆)
=
2
4
=
1
2
An experiment is carried out by tossing two fair coins. Find the probability
of obtaining
a) two heads
b) one head and tail
𝑃 𝐴 =
𝑛(𝐴)
𝑛(𝑆)
=
1
4
Let 𝑆 be the sample space of all outcomes:
So, 𝑛 𝑆 = 4
{ }𝑆 =
click on A and B
to see two subset of this sample space

20. Exercise
An experiment is carried out by tossing two fair dice.
the figure below shows the sample space of this experiment and A is the event
“obtaining the same number on both dice:
a)Find the probability of obtaining the same number on both dice

21. b)Find the probability of obtaining total sum of greater than 10
CONTINUE

22. Probability of Two Events Finding the probability of event A AND event B Occurring at the same
time.
In an experiment, a numbered card is pulled randomly from a bag. The cards are numb
1 to 10.
What is the probability that the card selected is a number more than 5 and an even
number?
Step 1, Finding S
Click on the elements of S
that are more than 5
{ }
{ }
P(A and B ) = P (A ∩ B )
Example
Step 2, Finding A

23. Event B:
Getting
even
Step 3, Finding B
Click on the
elements of S that
are Even
{ }
B={ }
𝐴 𝐵∙ 6
∙ 8
∙ 10
∙ 7
∙ 9
∙ 2
∙ 4
Venn diagram:
∙ 1 ∙ 3
∙ 5
{6,7,8,9,10} ∩ { 2,4,6,8, 10 } = {6,8, 10}
n(A ∩ B) =3
Step 4, Finding intersection of event A and event B
P(A ∩ B)= n (A ∩ B) / n(s) P(A ∩ B) = 3/ 10
Step 5 Finding the probability of event A AND event B, occurring at the same time

24. Probability of two events:
P(A or B)
Finding the probability of event A OR event B occurring at the same
time.
Elements of S less than 5 ,
Event of selecting an even number ,
1
2
4
3
6
8
10
5
7 9

25. Click here to find some
explanation
=
CONTINUE
Exercise

26. Sample space is the set of all the possible results in an experiment.
An event is a subset of the sample space.
𝑃 A =
number of elements in event A
total number of possible outcomes
=
𝑛(A)
𝑛(S)
Probability of an event A is given by:

27. Probability of event A and event B occurring at the same time can be calculated
if we know the number of elements in the intersection of sets A and B:
𝑃 𝐴 ∩ 𝐵 =
𝑛(𝐴 ∩ 𝐵)
𝑛(𝑆)
Probability of event 𝐴 or event 𝐵 occurring can be calculated if we know 𝑃 𝐴 ∩ 𝐵 :
𝑃 𝐴 ∪ 𝐵 = 𝑃 𝐴 + 𝑃 𝐵 − 𝑃(𝐴 ∩ 𝐵)
𝑃 𝐴 ∪ 𝐵 =
𝑛(𝐴 ∪ 𝐵)
𝑛(𝑆)
Probability of either event A or event B occurring can be calculated if we know the
number of elements in the union of sets A and B.
CONTINUE

28. Examples
Suppose you want to go on a picnic this afternoon,
and the weather report says that the chance of rain is
70%? Do you ever wonder where that 70% came
from?
If the meteorologist has data for 100 days with
similar weather conditions (the sample space and
therefore the denominator of our fraction), and on
70 of these days it rained (a favorable outcome),
the probability of rain on the next similar day is
70/100 or 70%.
CONTINUE

29. Play gamesClick on the “play games “ to find a
game