Dokumen tersebut membahas tentang ukuran penyebaran data statistika, termasuk definisi, contoh perhitungan, dan penjelasan mengenai ukuran penyebaran seperti range, deviasi rata-rata, varians, dan standar deviasi baik untuk data yang belum dikelompokkan maupun telah dikelompokkan."

1. Ukuran Statistika
Ukuran Penyebaran
Julius Nursyamsi

2. Pendahuluan
Ukuran penyebaran
 Suatu ukuran baik parameter atau statistik untuk
mengetahui seberapa besar penyimpangan data
dengan nilai rata – rata hitungnya
Ukuran penyebaran mencakup data
 Ungrouped data
 Data yang belum dikelompokan
 Grouped data
 Data yang telah dikelompokan ; Tabel distribusi
frekuensi

3. Ukuran Penyebaran
Ukuran penyebaran:
 Range
 Deviasi
 Rata – rata
 Varian
 Deviasi standar
 Range inter-kuartil
 Deviasi kuartil
Ukuran kecondongan dan keruncingan

4. Ukuran Penyebaran Untuk Data
Tidak Dikelompokan
Range – Jarak
 Merupakan perbedaan antara nilai terbesar
dan terkecil dalam suatu kelompok data baik
data populasi atau sampel
Rumusan Range
Range = Nilai terbesar – nilai terkecil
Perusahaan Harga Saham
Sentul City 530
Tunas Baru 580
Range
proteinprima 650
= 840 – 530
total 750
= 310
Mandiri 840

5. Deviasi Rata – rata Populasi
Rata – rata hitung dari nilai mutlak
deviasi antara nilai data pengamatan
dengan rata-rata hitungnya
Rumusan Deviasi rata –rata ( MD)
∑|x - x|
MD = X = Nilai data pengamatan
N X = Rata – rata hitung
N = Jumlah data

6. Contoh Deviasi Rata - Rata
Perusahaan Indek x-X Nilai Mutlak
Sentul City 7.5 1.14 1.14
Tunas Baru 8.2 1.84 1.84
proteinprima 7.8 1.44 1.44
total 4.8 -1.56 1.56
Mandiri 3.5 -2.86 2.86
Total 31.8 8.84
Rata -rata (X) 6.36 MD 1.768
MD =
= ∑|x - X| / n
= 8.84 / 5
= 1.768

7. Varians dan Standar Deviasi
Populasi
Varians
 Rata – rata hitung deviasi kuadrat setiap
data terhadap rata – rata hitungnya
Rumus varians populasi
)/N
(∑ X
∑(X - µ )2 µ=
σ 2=
N X = Nilai data pengamatan
µ = Nilai rata – rata hitung
N = Jumlah total data

8. Contoh Kasus Varians
Perusahaan Indek X-µ (X - µ)²
Sentul City 7.5 1.14 1.2996
Tunas Baru 8.2 1.84 3.3856
proteinprima 7.8 1.44 2.0736
total 4.8 -1.56 2.4336
Mandiri 3.5 -2.86 8.1796
Jumlah ( ∑X ) 31.8 ∑(X - µ)² 17.372
Rata - rata (µ) 6.36 σ² 3.4744
∑(X - µ )2 17.372
σ 2= = = 3.4744
N 5

9. Standar Deviasi
Standar deviasi
 Akar kuadrat dari varians dan menunjukan
standar penyimpangan data terhadap nilai
rata-ratanya
Rumus standar deviasi
∑(X - µ )2
σ=√ atau σ = √ σ²
N

10. Contoh Kasus Standar
Deviasi
Nilai varians :
∑(X - µ )2 17.372
σ 2= = = 3.4744
N 5
Nilai standar deviasi :
σ = √ 3.4744 = 1.864
Nilai penyimpangan sebesar 1.864

11. Varians dan Standar Deviasi Sampel
Varians
∑(x - x )2
s 2=
n -1
Standar deviasi
S = √ s²

12. Contoh Kasus Sampel
Harga
No Perusahaan saham x-X (x - X)² Varians :
1 Jababeka 215 -358 128164 ∑(x – X)²
2 Indofarma 290 -283 80089
s² =
3 Budi Acid 310 -263 69169
4 Kimia farma 365 -208 43264
n–1
5 Sentul City 530 -43 1849 s² = 824260 / 9
6 Tunas Baru 580 7 49 s² = 91584.44
7 proteinprima 650 77 5929
8 total 750 177 31329
9 Mandiri 840 267 71289 Standar deviasi :
10 Panin 1200 627 393129 S = √ s²
Jumlah 5730 824260 S = √ 91584.44
Rata - Rata (X) 573 s² 91584.44
S = 302.63
S 302.63

13. Ukuran Penyebaran Untuk Data
dikelompokan
Range – Jarak
 Merupakan selisih antara batas atas
dari kelas tertinggi dengan batas bawah
dari kelas terendah
Rumusan Range
Range = Batas atas kelas tertinggi –
nilai terkecil

14. Contoh Range
Batas atas
Kelas Interval Kelas terendah
1 215 2122 Batas atas
Kelas tertinggi
2 2123 4030
3 4031 5938
4 5939 7846 Range :
= 9754 – 215
5 7847 9754 = 9539

15. Deviasi Rata - Rata
Rumus deviasi rata - rata
∑ f. |x - x|
MD =
n
Rata – rata hitung data dikelompokan
x = (∑ f.x ) / n

16. Contoh Kasus
Interval Titik tengah
Kelas Kelas f (x) f.x |x - X| f.|x - X|
1 16 24 10 20 200 13.68 136.8
2 25 33 18 29 522 4.68 84.24
3 34 42 14 38 532 4.32 60.48
4 43 51 4 47 188 13.32 53.28
5 52 60 2 56 112 22.32 44.64
6 61 69 2 65 130 31.32 62.64
Total 50 255 1684 89.64 442.08
Rata - rata
(X) 33.68
MD = (∑f.|x - X|) / n = 442.08 / 50 = 8.8416

17. Varians dan Standar Deviasi data di
kelompokan
Varians
∑f. (x - x )2
s 2=
n -1
Standar deviasi
S = √ s²

18. Contoh Kasus
Titik tengah
Kelas Interval Kelas f (x) f.x |x - X| |x - X|² f.|x - X|²
1 16 24 10 20 200 13.68 187.1424 1871.424
2 25 33 18 29 522 4.68 21.9024 394.2432
3 34 42 14 38 532 4.32 18.6624 261.2736
4 43 51 4 47 188 13.32 177.4224 709.6896
5 52 60 2 56 112 22.32 498.1824 996.3648
6 61 69 2 65 130 31.32 980.9424 1961.885
Total 50 255 1684 89.64 1884.254 6194.88
Rata - rata (X) 33.68
Varians : Standar deviasi :
s²= (∑f.|x - X|²)/ n – 1 S = √ s²
= 6194.88 / 49 = √ 126.4261
= 126.4261 = 11.2439

19. Ukuran Penyebaran Relatif
Mengubah ukuran penyebaran menjadi
persentase atau ukuran relatif
Penggunaan ukuran relatif memberikan
manfaat :
 Data mempunyai satuan penguikuran yang
berbeda
 Data mempunyai satuan ukuran yang
sama

20. Ukuran Penyebaran Relatif
Koefisien range
Koefisien deviasi rata-rata
Koefisien deviasi standar

21. Koefisien Range
Pengukuran penyebaran dengan
menggunakan range secara relatif
Rumusan :
KR = ( (la – Lb) / (La + Lb) ) x 100 %
La : Batas atas data atau kelas tertinggi
Lb : Batas bawah data atau kelas terendah

22. Contoh Koefisien Range
Interval
KR :
Kelas Kelas f
= (La – Lb) / (La + Lb)
1 16 24 10
= (69 – 16 ) / (69 + 16)
2 25 33 18
= 53 / 85
3 34 42 14
= 0.6235 x 100 %
4 43 51 4
= 62.35 %
5 52 60 2
6 61 69 2
La : Kelas tertinggi = 69
Lb : Kelas terendah = 16

23. Koefisien Deviasi Rata - Rata
Koefisien deviasi rata – rata
 Ukuran penyebaran dengan menggunakan
deviasi rata-rata relatif terhadap nilai rata-
ratanya atau persentase dari deviasi rata-
rata terhadap nilai rata-ratanya
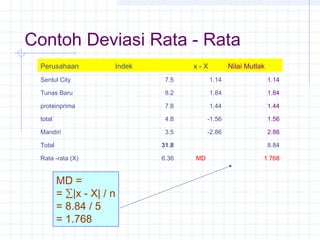
Rumus :
KMD = [ MD / x ] x 100%
MD = Deviasi rata - rata
X = Nilai rata – rata data

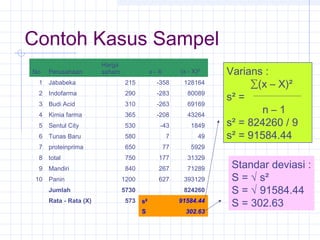
24. Contoh Kasus
Data dikelompokan :
 MD = 8.8416
 X = 33.68
Koefisien deviasi rata – rata :
KMD = [ 8.8416 / 33.68 ] x 100 %
= 0.2625 x 100 %
= 26.25 %

25. Koefisien Standar Deviasi
Koefisien standar deviasi
 Ukuran penyebaran yang menggunakan
standar deviasi relatif terhadap nilai rata-
rata yang dinyatakan sebagai persentase
Rumus
KSD = [ s / x ] x 100 %
S = Standar deviasi
X = Nilai rata – rata data

26. Contoh Kasus
Data dikelompokan
 Standar deviasi = 11.2439
 Rata – Rata hitung (x) = 33.68
 Nilai koefisien stnadar deviasi
KSD = [ s / x ] x 100 %
= [ 11.2439 / 33.68 ] x 100%
= 0.3338 x 100 %
= 33.38 %

27. Ukuran Kecondongan -
Skewness
Ukuran kecondongan – kemencengan
 Kurva tidak simetris
Pada kurva distribusi frekuensi
diketahui dari posisi modus, rata-rata
dan media
Pendekatan : Jika
 Rata-rata = median = modus : Simetris
 Rata-rata < median < modus : Menceng ke kiri
 Rata-rata > median > modus : Menceng ke kanan

28. Koefisien Skewness
Sk = [µ - Mo ] / σ atau = 3.[µ - Md] / σ
Contoh kasus data dikelompokan µ = Nilai rata – rata hitung
Mo = Nilai modus
µ = 33.68 Md = Nilai median
Mo = 18 σ = Standar deviasi
Md = 32
σ = 11.2439
Sk = {3. [ 33.68 – 32]}
Sk = [33.68- 18 ] / 11.2439 11.2439
Sk = 15.68 / 11.2439 Sk = 5.04 / 11.2439
Sk = 1.394 Sk = 0.4482

29. Ukuran Keruncingan -
Kurtosis
Keruncingan disebut juga ketinggian
kurva
Pada distribusi frekuensi di bagi dalam
tiga bagian :
 Leptokurtis = Sangat runcing
 Mesokurtis = Keruncingan sedang
 Platykurtis = Kurva datar

30. Koefisien Kurtosis
Bentuk kurva keruncingan – kurtosis
 Mesokurtik α4 = 3
 Leptokurtik α4 > 3
Nilai data
 Platikurtik α4 < 3
Koefisien kurtosis (data tidak
dikelompokan)
1/n ∑(x - µ)4
α4 =
σ4

31. Koefisien Kurtosis
Koefisien kurtosis (data dikelompokan)
1/n ∑ f. (X - µ)4
α4 =
σ4
Jumlah Frekuensi
Standar deviasi Nilai rata – rata hitung
Nilai tengah kelas

32. Rata – Rata Geometrik
Digunakan untuk menghitung rata-rata
laju pertumbuhan – Growth rate
Rumus :
G = n√ (x1 . x2 . x3 . … xn )
G = [log x1 + log x2 +… log xn]
n
G = Antilog (log G)

33. Contoh
Data pertumbuhan suku bunga selama
5 hari, yaitu 1.5, 2.3, 3.4, 1.2, 2.5 %
Tingkat pertumbuhan :
G = [log 1.5 + log 2.3 +log 3.4 +
log 1.2 + log 2.5 ] / 5
G = [ 0.176 + 0.361 + 0.531 + 0.079
+ 0.397] / 5
G = 1.5464 / 5 = 0.30928
G = antilog 0.30928 = 2.03

34. Ukuran Penyebaran Lain
Range Inter-Kuartil
 Jarak inter-kuartil = K3 – K1
Jika :
 Inter-kuartil : Nilainya lebih kecil ; Bahwa
data dalam sampel dan populasi lebih
mengelompok ke nilai rata-rata hitung
(seragam)
 Inter-kuartil : lebih besar ; Kurang seragam

35. Ukuran Penyebaran Lain
Deviasi Kuartil
 Setengah jarak antara kuartil ke 3 dan
kuartil ke 1
Rumusan Deviasi kuartil – DK
DK = [ K3 – K1 ] / 2
Jika
 DK lebih kecil ; Rata – rata data lebih
mewakili keseluruhan data

36. Ukuran Penyebaran Lain
Jarak persentil
 Selisih antara persentil ke 90 dengan
persentil ke 10
Rumusan jarak persentil - JP
JP = P90 – P10
Jika JP lebih besar
 Bahwa nilai deviasi lebih besar