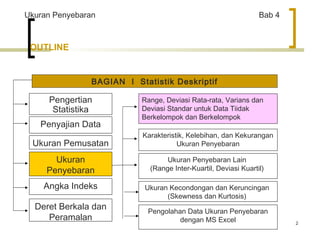
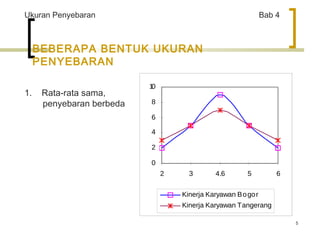
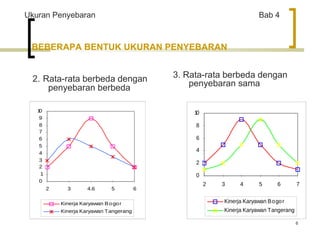
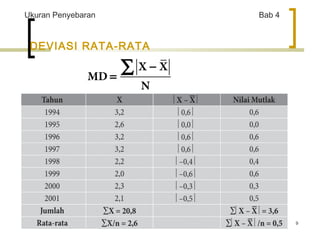
Dokumen ini membahas ukuran penyebaran dalam statistik, mencakup pengertian, rumus, dan aplikasi berbagai ukuran seperti deviasi standar, varians, dan range. Diberikan pula contoh perhitungan serta penggunaan MS Excel untuk pengolahan data. Selain itu, dijelaskan tentang kecondongan dan keruncingan data dengan contoh spesifik dari berbagai negara.











![17
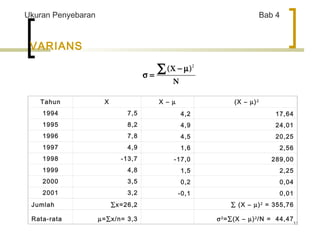
Ukuran Penyebaran Bab 4
UKURAN PENYEBARAN RELATIF
a. Koefisien Range
RUMUS:
La -
Lb
KR =
x 100
%
La +
Lb
Contoh:
Range Harga Saham = [(878-160)/(878+160)]x100 = 69,17%
Jadi jarak nilai terendah dan tertinggi harga saham adalah 69,17%.
b. Koefisien Deviasi Rata-rata
RUMUS:
= MD
KMD x 100
%
X
Contoh:
Pertumbuhan ekonomi negara maju=(0,56/2,6) x 100 = 19,23%
Jadi penyebaran pertumbuhan ekonomi dari nilai tengahnya sebesar
19,23%, bandingkan dengan Indonesia yang sebesar 130,30%.](https://image.slidesharecdn.com/bab04-statistika-141122005239-conversion-gate01/85/Bab-04-statistika-17-320.jpg)