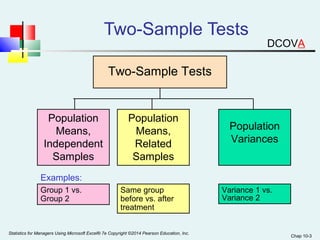
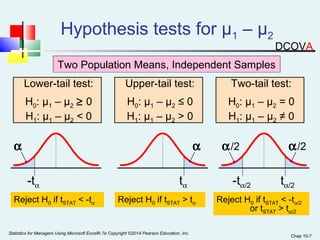
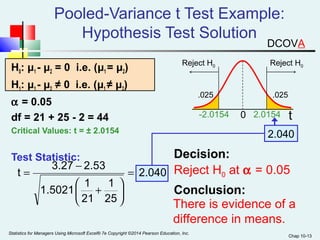
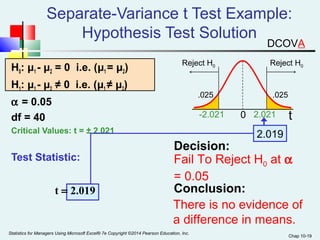
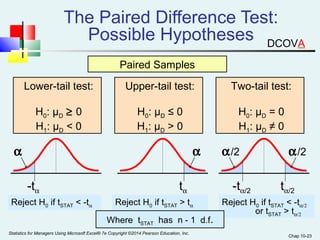
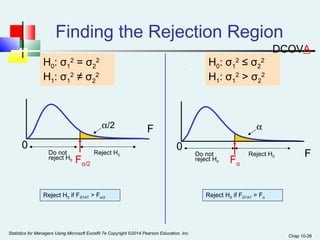
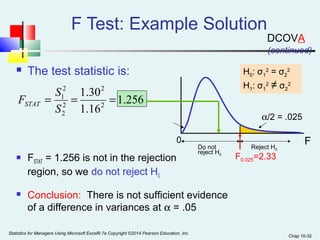
This chapter discusses hypothesis testing for comparing means and variances between two populations or samples. It covers testing for the difference between two independent population means, two related (paired) population means, and two independent population variances. The key tests covered are the pooled variance t-test and separate variance t-test for independent samples, and the paired t-test for related samples. Examples are provided to demonstrate how to calculate the test statistic and conduct the hypothesis test to determine if the means or variances are significantly different.

1. Statistics for Managers Using
Microsoft Excel
7th Edition
Chapter 10
Two-Sample Tests
Statistics for Managers Using Microsoft Excel® 7e Copyright ©2014 Pearson Education, Inc. Chap 10-1

2. Chap 10-2
Learning Objectives
In this chapter, you learn:
 How to use hypothesis testing for comparing the
difference between
 The means of two independent populations
 The means of two related populations
 The variances of two independent populations
Statistics for Managers Using Microsoft Excel® 7e Copyright ©2014 Pearson Education, Inc.

3. Chap 10-3
Two-Sample Tests
Two-Sample Tests
Population
Means,
Independent
Samples
Population
Means,
Related
Samples
Population
Variances
Group 1 vs.
Group 2
Same group
before vs. after
treatment
Variance 1 vs.
Variance 2
Examples:
Statistics for Managers Using Microsoft Excel® 7e Copyright ©2014 Pearson Education, Inc.
DCOVA

4. Difference Between Two Means
Chap 10-4
Population means,
independent
samples
Goal: Test hypothesis or form
a confidence interval for the
difference between two
population means, μ1 – μ2
The point estimate for the
difference is
X1 – X2
*
σ1 and σ2 unknown,
assumed equal
σ1 and σ2 unknown,
not assumed equal
Statistics for Managers Using Microsoft Excel® 7e Copyright ©2014 Pearson Education, Inc.
DCOVA

5. Chap 10-5
Difference Between Two Means:
Independent Samples
Population means,
independent
samples *
 Different data sources
 Unrelated
 Independent
 Sample selected from one
population has no effect on the
sample selected from the other
population
Use Sp to estimate unknown
σ. Use a Pooled-Variance t
test.
σ1 and σ2 unknown,
assumed equal
σ1 and σ2 unknown,
not assumed equal
Use S1 and S2 to estimate
unknown σ1 and σ2. Use a
Separate-variance t test
Statistics for Managers Using Microsoft Excel® 7e Copyright ©2014 Pearson Education, Inc.
DCOVA

6. Chap 10-6
Hypothesis Tests for
Two Population Means
Two Population Means, Independent Samples
Lower-tail test:
H0: μ1 ³ μ2
H1: μ1 < μ2
i.e.,
H0: μ1 – μ2 ³ 0
H1: μ1 – μ2 < 0
Upper-tail test:
H0: μ1 ≤ μ2
H1: μ1 > μ2
i.e.,
H0: μ1 – μ2 ≤ 0
H1: μ1 – μ2 > 0
Two-tail test:
H0: μ1 = μ2
H1: μ1 ≠ μ2
i.e.,
H0: μ1 – μ2 = 0
H1: μ1 – μ2 ≠ 0
Statistics for Managers Using Microsoft Excel® 7e Copyright ©2014 Pearson Education, Inc.
DCOVA

7. Chap 10-7
Hypothesis tests for μ1 – μ2
Two Population Means, Independent Samples
Lower-tail test:
H0: μ1 – μ2 ³ 0
H1: μ1 – μ2 < 0
Upper-tail test:
H0: μ1 – μ2 ≤ 0
H1: μ1 – μ2 > 0
Two-tail test:
H0: μ1 – μ2 = 0
H1: μ1 – μ2 ≠ 0
a a a/2 a/2
-ta -ta/2 ta ta/2
Reject H0 if tSTAT < -ta Reject H0 if tSTAT > ta Reject H0 if tSTAT < -ta/2
or tSTAT > ta/2
Statistics for Managers Using Microsoft Excel® 7e Copyright ©2014 Pearson Education, Inc.
DCOVA

8. Hypothesis tests for μ1 - μ2 with σ1 and
Chap 10-8
σ2 unknown and assumed equal
Population means,
independent
samples
Assumptions:
 Samples are randomly and
independently drawn
 Populations are normally
distributed or both sample
sizes are at least 30
 Population variances are
unknown but assumed equal
σ * 1 and σ2 unknown,
assumed equal
σ1 and σ2 unknown,
not assumed equal
Statistics for Managers Using Microsoft Excel® 7e Copyright ©2014 Pearson Education, Inc.
DCOVA

9. Hypothesis tests for μ1 - μ2 with σ1
and σ2 unknown and assumed equal
(continued)
- - -
X X μ μ
1 2 1 2
ö
Chap 10-9
Population means,
independent
samples
• The pooled variance is:
( ) 2
( )
(n n 1)
S = n - 1S + n -
1S
2 1 1
p - + -
2 2
1) (
1 2
• The test statistic is:
2
æ
1
S 1
• Where tSTAT has d.f. = (n1 + n2 – 2)
σ * 1 and σ2 unknown,
assumed equal
σ1 and σ2 unknown,
not assumed equal
( ) ( )
÷ ÷ø
ç çè
+
=
1 2
2p
STAT
n
n
t
Statistics for Managers Using Microsoft Excel® 7e Copyright ©2014 Pearson Education, Inc.
DCOVA

10. Confidence interval for μ1 - μ2 with σ1
and σ2 unknown and assumed equal
The confidence interval for
1
Chap 10-10
Population means,
independent
samples
÷ø
( ) ÷ æ
ö
X X tα
S 1 ç çè
- ± +
1 2
2p
1 2 /2 n
n
μ1 – μ2 is:
Where tα/2 has d.f. = n1 + n2 – 2
*
σ1 and σ2 unknown,
assumed equal
σ1 and σ2 unknown,
not assumed equal
Statistics for Managers Using Microsoft Excel® 7e Copyright ©2014 Pearson Education, Inc.
DCOVA

11. Pooled-Variance t Test Example
Chap 10-11
You are a financial analyst for a brokerage firm. Is there
a difference in dividend yield between stocks listed on the
NYSE & NASDAQ? You collect the following data:
NYSE NASDAQ
Number 21 25
Sample mean 3.27 2.53
Sample std dev 1.30 1.16
Assuming both populations are
approximately normal with
equal variances, is
there a difference in mean
yield (a = 0.05)?
Statistics for Managers Using Microsoft Excel® 7e Copyright ©2014 Pearson Education, Inc.
DCOVA

12. The test statistic is:
( ) ( ) ( ) 2.040
Chap 10-12
Pooled-Variance t Test Example:
Calculating the Test Statistic
= - -
3.27 2.53 0
- - -
1 2 1 2 =
1
1.5021 1
X X μ μ
1
æ
S 1
ö çè
ö
( ) ( ) ( ) ( = 21 - 11.30 + 25 -
11.16
) 1.5021
(21-1) (25 1)
S = n - 1S + n -
1S
(n 1) (n 1)
2 2
1 2
2
2 2
2
2 1 1
p =
+ -
- + -
25
21
n
n
t
1 2
2p
÷ø
æ +
÷ ÷ø
ç çè
+
=
(continued)
H0: μ1 - μ2 = 0 i.e. (μ1 = μ2)
H1: μ1 - μ2 ≠ 0 i.e. (μ1 ≠ μ2)
Statistics for Managers Using Microsoft Excel® 7e Copyright ©2014 Pearson Education, Inc.
DCOVA

13. Reject H0 Reject H0
-2.0154 0 2.0154 t
Reject H0 at a = 0.05
There is evidence of a
difference in means.
Chap 10-13
Pooled-Variance t Test Example:
Hypothesis Test Solution
H0: μ1 - μ2 = 0 i.e. (μ1 = μ2)
H1: μ1 - μ2 ≠ 0 i.e. (μ1 ≠ μ2)
a = 0.05
df = 21 + 25 - 2 = 44
Critical Values: t = ± 2.0154
Test Statistic: Decision:
Conclusion:
.025
.025
2.040
2.040
t 3.27 2.53 =
1
= -
ö 25
çè
1.5021 1
21
÷ø
æ +
Statistics for Managers Using Microsoft Excel® 7e Copyright ©2014 Pearson Education, Inc.
DCOVA

14. Chap 10-14
Pooled-Variance t Test Example:
Confidence Interval for μ1 - μ2
Since we rejected H0 can we be 95% confident that μNYSE >
μNASDAQ?
95% Confidence Interval for μNYSE - μNASDAQ
( ) 1
ö
0.74 2.0154 0.3628 (0.009, 1.471)
ç çè æ
1 2 = ± ´ = ÷ ÷ø
/2 n
X X S 1
- ± + a t
n
1 2
2p
Since 0 is less than the entire interval, we can be 95%
Statistics for Managers Using Microsoft Excel® 7e Copyright ©2014 Pearson Education, Inc.
DCOVA

15. Hypothesis tests for μ1 - μ2 with σ1
and σ2 unknown, not assumed equal
Chap 10-15
Population means,
independent
samples
Assumptions:
 Samples are randomly and
independently drawn
 Populations are normally
distributed or both sample
sizes are at least 30
 Population variances are
unknown and cannot be
assumed * to be equal
σ1 and σ2 unknown,
assumed equal
σ1 and σ2 unknown,
not assumed equal
Statistics for Managers Using Microsoft Excel® 7e Copyright ©2014 Pearson Education, Inc.
DCOVA

16. Hypothesis tests for μ1 - μ2 with σ1 and
σ2 unknown and not assumed equal
t = X - X - μ -
μ
1 2 1 2
Chap 10-16
Population means,
independent
samples
(continued)
*
σ1 and σ2 unknown,
assumed equal
σ1 and σ2 unknown,
not assumed equal
The test statistic is:
( ) ( )
22
2
2
1
1
STAT
S
n
S
n
+
tSTAT has d.f. ν =
2
2
S
ö
2
2
n
S
ö
æ
+
n 1
æ
S
2
1
n
S
2
1
ö
æ
n 1
n
n
2
2
2
1
2
1
2
2
1
-
÷ ÷ø
ç çè
-
÷ ÷ø
ç çè
÷ ÷ø
ç çè
+
n =
DCOVA
Statistics for Managers Using Microsoft Excel® 7e Copyright ©2014 Pearson Education, Inc.

17. Separate-Variance t Test Example
Chap 10-17
You are a financial analyst for a brokerage firm. Is there
a difference in dividend yield between stocks listed on the
NYSE & NASDAQ? You collect the following data:
NYSE NASDAQ
Number 21 25
Sample mean 3.27 2.53
Sample std dev 1.30 1.16
Assuming both populations are
approximately normal with
unequal variances, is
there a difference in mean
yield (a = 0.05)?
Statistics for Managers Using Microsoft Excel® 7e Copyright ©2014 Pearson Education, Inc.
DCOVA

18. Separate-Variance t Test Example:
Chap 10-18
Calculating the Test Statistic
The test statistic is:
( ) ( ) ( ) = 3.27 - 2.53 -
0
2.019
= - - -
1 2 1 2 =
1.16
25
1.30
21
t X X μ μ
S
n
S
2
1
n
2 2
22
2
1
ö
÷ ÷ø
æ
ç çè
+
ö
÷ ÷ø
æ
ç çè
+
(continued)
H0: μ1 - μ2 = 0 i.e. (μ1 = μ2)
H1: μ1 - μ2 ≠ 0 i.e. (μ1 ≠ μ2)
2 2 2
1.16
ö
1.16
25
1.30
æ
1.30
21
2
2
S
ö
2
2
n
æ
S
2
1
n
S
S
2
1
ö
æ
+
ö
æ
ö
æ
+
ö
æ
Statistics for Managers Using Microsoft Excel® 7e Copyright ©2014 Pearson Education, Inc.
DCOVA
40.57
24
20
25
21
n 1
n 1
n
n
2 2 2 2
2
2
2
1
2
1
2
2
1
=
÷ ÷ø
ç çè
÷ ÷ø
ç çè
÷ ÷ø
ç çè
+
=
-
÷ ÷ø
ç çè
-
÷ ÷ø
ç çè
÷ ÷ø
ç çè
+
n = Use degrees of
freedom = 40

19. Separate-Variance t Test Example:
Reject H0 Reject H0
-2.021 0 2.021 t
Fail To Reject H0 at a
= 0.05
There is no evidence of
a difference in means.
Chap 10-19
Hypothesis Test Solution
H0: μ1 - μ2 = 0 i.e. (μ1 = μ2)
H1: μ1 - μ2 ≠ 0 i.e. (μ1 ≠ μ2)
a = 0.05
df = 40
Critical Values: t = ± 2.021
Test Statistic:
Decision:
Conclusion:
.025
.025
2.019
t = 2.019
Statistics for Managers Using Microsoft Excel® 7e Copyright ©2014 Pearson Education, Inc.
DCOVA

20. Chap 10-20
Related Populations
The Paired Difference Test
Tests Means of 2 Related Populations
 Paired or matched samples
 Repeated measures (before/after)
 Use difference between paired values:
 Eliminates Variation Among Subjects
 Assumptions:
 The difference is Normally Distributed
 Or, if not Normal, use large samples
Related
samples
Di = X1i - X2i
Statistics for Managers Using Microsoft Excel® 7e Copyright ©2014 Pearson Education, Inc.
DCOVA

21. (D D)
Chap 10-21
Related Populations
The Paired Difference Test
The ith paired difference is Di , where
Related
samples
Di = X1i - X2i
i å=
=
The point estimate for the
paired difference
population mean μD is D : n
D
D
n
i 1
=
n is the number of pairs in the paired sample
-
n 1
S
n
å=
i 1
2
i
D -
The sample standard
deviation is SD
(continued)
Statistics for Managers Using Microsoft Excel® 7e Copyright ©2014 Pearson Education, Inc.
DCOVA

22. Chap 10-22
The Paired Difference Test:
Finding tSTAT
 The test statistic for μD is:
Paired
samples
t D μ
n
S
D
STAT
D = -
 Where tSTAT has n - 1 d.f.
Statistics for Managers Using Microsoft Excel® 7e Copyright ©2014 Pearson Education, Inc.
DCOVA

23. Chap 10-23
The Paired Difference Test:
Possible Hypotheses
Lower-tail test:
H0: μD ³ 0
H1: μD < 0
Upper-tail test:
H0: μD ≤ 0
H1: μD > 0
Two-tail test:
H0: μD = 0
H1: μD ≠ 0
Paired Samples
a a a/2 a/2
-ta -ta/2 ta ta/2
Reject H0 if tSTAT < -ta Reject H0 if tSTAT > ta Reject H0 if tSTAT < -ta/2
or tSTAT > ta/2
Where tSTAT has n - 1 d.f.
Statistics for Managers Using Microsoft Excel® 7e Copyright ©2014 Pearson Education, Inc.
DCOVA

24. Chap 10-24
The Paired Difference
Confidence Interval
Paired The confidence interval for μD is
samples
(D -
D)
n 1
S
n
å=
i 1
2
i
SD
n
=
D -
a / 2 D ± t
where
Statistics for Managers Using Microsoft Excel® 7e Copyright ©2014 Pearson Education, Inc.
DCOVA

25.  Assume you send your salespeople to a “customer
service” training workshop. Has the training made a
difference in the number of complaints? You collect
the following data:
= -4.2
(D -
D)
Chap 10-25
Paired Difference Test:
Example
Number of Complaints: (2) - (1)
Salesperson Before (1) After (2) Difference, Di
C.B. 6 4 - 2
T.F. 20 6 -14
M.H. 3 2 - 1
R.K. 0 0 0
M.O. 4 0 - 4
-21
D =
S Di
n
5.67
n 1
S
2
i
D
=
-
= å
Statistics for Managers Using Microsoft Excel® 7e Copyright ©2014 Pearson Education, Inc.
DCOVA

26. Chap 10-26
Paired Difference Test:
Solution
 Has the training made a difference in the number of
complaints (at the 0.01 level)?
H0: μD = 0
H1: μD ¹ 0
D = - 4.2
1.66
t0.005 = ± 4.604
d.f. = n - 1 = 4
Test Statistic:
4.2 0
5.67/ 5
t μ
S / n
D
STAT
= D - D = - - = -
Reject
a/2
Reject
a/2
- 4.604 4.604
- 1.66
Decision: Do not reject H0
(tstat is not in the reject region)
Conclusion: There is not a
significant change in the
number of complaints.
a = .01
Statistics for Managers Using Microsoft Excel® 7e Copyright ©2014 Pearson Education, Inc.
DCOVA

27. Chap 10-27
Testing for the Ratio Of Two
Population Variances
Tests for Two
Population
Variances
F test statistic
* Hypotheses FSTAT
H: σ2 = σ2
01
2
H1: σ1
2 ≠ σ2
2
H0: σ1
2 ≤ σ2
2
H1: σ1
2 > σ2
2
S1
2 / S2
2
Where:
S2 = Variance of sample 1 (the larger sample variance)
1
n= sample size of sample 1
1 S2
2 = Variance of sample 2 (the smaller sample variance)
n2 = sample size of sample 2
n1 –1 = numerator degrees of freedom
n2 – 1 = denominator degrees of freedom
Statistics for Managers Using Microsoft Excel® 7e Copyright ©2014 Pearson Education, Inc.
DCOVA

28. The F Distribution
 The F critical value is found from the F table
 There are two degrees of freedom required: numerator
and denominator
 The larger sample variance is always the numerator
Chap 10-28
 When
F S STAT =
 In the F table,
2
1
S
df1 = n1 – 1 ; df2 = n2 – 1 2
2
 numerator degrees of freedom determine the column
 denominator degrees of freedom determine the row
Statistics for Managers Using Microsoft Excel® 7e Copyright ©2014 Pearson Education, Inc.
DCOVA

29. Chap 10-29
Finding the Rejection Region
H: σ2 = σ2
01
2
H1: σ1
2 ≠ σ2
2
H0: σ1
2 ≤ σ2
2
H1: σ1
2 > σ2
2
a
0 F
Do not
Reject Hreject H0 0
Fα Reject H0 if FSTAT > Fα
F
0
a/2
Reject H0 Do not
reject H0 Fα/2
Reject H0 if FSTAT > Fα/2
Statistics for Managers Using Microsoft Excel® 7e Copyright ©2014 Pearson Education, Inc.
DCOVA

30. Chap 10-30
F Test: An Example
You are a financial analyst for a brokerage firm. You
want to compare dividend yields between stocks listed on
the NYSE & NASDAQ. You collect the following data:
NYSE NASDAQ
Number 21 25
Mean 3.27 2.53
Std dev 1.30 1.16
Is there a difference in the
variances between the NYSE
& NASDAQ at the a = 0.05 level?
Statistics for Managers Using Microsoft Excel® 7e Copyright ©2014 Pearson Education, Inc.
DCOVA

31. Chap 10-31
F Test: Example Solution
 Form the hypothesis test:
H0: σ2
1 = σ2
2 (there is no difference between variances)
H1: σ2
1 ≠ σ2
2 (there is a difference between variances)
 Find the F critical value for a = 0.05:
 Numerator d.f. = n1 – 1 = 21 –1 =20
 Denominator d.f. = n2 – 1 = 25 –1 = 24
 Fα/2 = F.025, 20, 24 = 2.33
Statistics for Managers Using Microsoft Excel® 7e Copyright ©2014 Pearson Education, Inc.
DCOVA

32. Chap 10-32
 The test statistic is:
0
1.256
1.30
= 1 = =
S
1.16
2
2
2
2
2
F S STAT
H0: σ1
2 = σ2
a/2 = .025
Reject H0 Do not
reject H0
F0.025=2.33
2
H1: σ1
2 ≠ σ2
2
F Test: Example Solution
 FSTAT = 1.256 is not in the rejection
region, so we do not reject H0
(continued)
 Conclusion: There is not sufficient evidence
of a difference in variances at a = .05
F
Statistics for Managers Using Microsoft Excel® 7e Copyright ©2014 Pearson Education, Inc.
DCOVA

33. Chap 10-33
Chapter Summary
In this chapter we discussed
 Comparing two independent samples
 Performed pooled-variance t test for the difference in
two means
 Performed separate-variance t test for difference in two
means
 Formed confidence intervals for the difference between
two means
 Comparing two related samples (paired
samples)
 Performed paired t test for the mean difference
 Formed confidence intervals for the mean difference
Statistics for Managers Using Microsoft Excel® 7e Copyright ©2014 Pearson Education, Inc.

34. (continued)
Chap 10-34
Chapter Summary
 Performing an F test for the ratio of two
population variances
Statistics for Managers Using Microsoft Excel® 7e Copyright ©2014 Pearson Education, Inc.