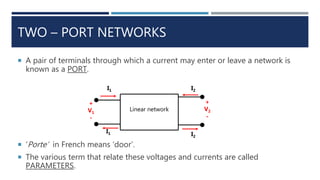
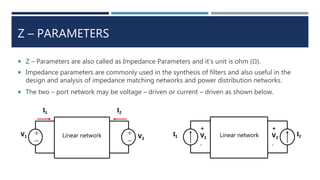
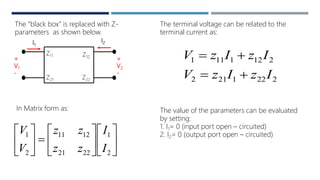
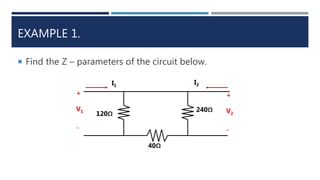
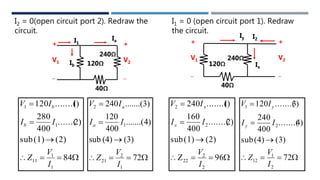
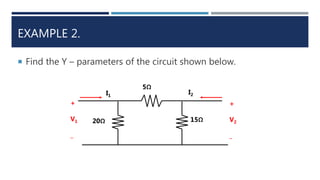
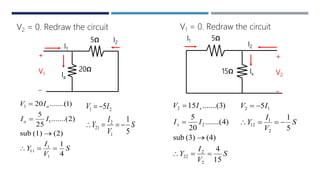
This document discusses two-port networks and their parameters. It defines a two-port network as having two ports through which current can enter or leave. The document introduces Z-parameters and Y-parameters as ways to relate the voltages and currents in a linear two-port network. Z-parameters express the terminal current in terms of voltage, while Y-parameters express the terminal voltage in terms of current. The document provides examples of calculating the Z-parameters and Y-parameters of simple resistor networks by opening or shorting the ports.

1. TWO PORT NETWORKS
Presented By:
Rohan Kaushik (161310109051)
Aakash Dhariwal (161310109001)
Nayan Purohit (161310109045)

2. CONTENTS:
 TWO – PORT NETWORKS AND ITS FUNTIONS.
 Z – PARAMETERS.
 Y – PARAMETERS.

3. TWO – PORT NETWORKS
 A pair of terminals through which a current may enter or leave a network is
known as a PORT.
 ‘Porte’ in French means ‘door’.
 The various term that relate these voltages and currents are called
PARAMETERS.
Linear network
+
V1
-
I1
I1 I2
I2
+
V2
-

4. WHY TO STUDY TWO – PORT NETWORKS?
 Practical networks are huge and very complex. There are many types of
networks that computer can't understand. So we need to construct a
systematic model for any network
 We can model any electronic device to two port network from that it is very
simple to analyse the device properties and get clear vision of internal
working of electronic device.

5. Z – PARAMETERS
 Z – Parameters are also called as Impedance Parameters and it’s unit is ohm (Ω).
 Impedance parameters are commonly used in the synthesis of filters and also useful in the
design and analysis of impedance matching networks and power distribution networks.
 The two – port network may be voltage – driven or current – driven as shown below.
Linear network
I1 I2
+

+

V1 V2
I1 I2
+
V1
-
Linear network
+
V2
-

6. +
V1
-
I1
I2
+
V2
-
Z11
Z21
Z12
Z22
The “black box” is replaced with Z-
parameters as shown below.
The terminal voltage can be related to the
terminal current as:
2221212
2121111
IzIzV
IzIzV




















2
1
2221
1211
2
1
I
I
zz
zz
V
V
In Matrix form as: The value of the parameters can be evaluated
by setting:
1. I1= 0 (input port open – circuited)
2. I2= 0 (output port open – circuited)

7. The Z-parameters that we want to determine are z11, z12, z21, z22.
01
2
21
01
1
11
2
2




I
I
I
V
z
I
V
z
02
2
22
02
1
12
1
1




I
I
I
V
z
I
V
z
z11 = open – circuit input impedance.
z12 = open – circuit transfer impedance from port 1 to port 2.
z21 = open – circuit transfer impedance from port 2 to port 1.
z22 = open – circuit output impedance.

8. EXAMPLE 1.
 Find the Z – parameters of the circuit below.
40Ω
240Ω
120Ω
+
V1
_
+
V2
_
I1
I2

9. I2 = 0(open circuit port 2). Redraw the
circuit.
40Ω
240Ω
120Ω
+
V1
_
+
V2
_
I1
Ia
Ib




84
(2)(1)sub
)2......(
400
280
)1.......(120
1
1
11
1
1
I
V
Z
II
IV
b
b




72
(3)(4)sub
)4.......(
400
120
.......(3)240
1
2
21
1
2
I
V
Z
II
IV
a
a
I1 = 0 (open circuit port 1). Redraw
the circuit.
40Ω
240Ω
120Ω
+
V1
_
+
V2
_
Iy I2
Ix




96Z
(2)(1)sub
)2.......(
400
160
)1.......(240
2
2
22
2
2
I
V
II
IV
x
x




72
(3)(4)sub
)4.......(
400
240
)3.......(120
2
1
12
2
1
I
V
Z
II
IV
y
y

10. Y - PARAMETERS
 Y – parameters also called admittance parameters and it’s unit is siemens (S).
+
V1
-
I1
I2
+
V2
-
Y11
Y21
Y12
Y22
The terminal current can be expressed in term
of terminal voltage as:
2221212
2121111
VyVyI
VyVyI


In Matrix Form:


















2
1
2221
1211
2
1
V
V
yy
yy
I
I

11. The Y-parameters that we want to determine are Y11, Y12, Y21, Y22.
The values of the parameters can be evaluate by setting:
i) V1 = 0 (input port short – circuited).
ii) V2 = 0 (output port short – circuited).
01
2
21
01
1
11
2
2




V
V
V
I
Y
V
I
Y
02
2
22
02
1
12
1
1




V
V
V
I
Y
V
I
Y

12. EXAMPLE 2.
 Find the Y – parameters of the circuit shown below.
5Ω
15Ω20Ω
+
V1
_
+
V2
_
I1
I2

13. 5Ω
20Ω
+
V1
_
I1
I2
Ia
V2 = 0. Redraw the circuit
S
V
I
Y
II
IV
a
a
4
1
(2)(1)sub
)2.......(
25
5
)1.......(20
1
1
11
1
1




S
V
I
Y
IV
5
1
5
1
2
21
21


V1 = 0. Redraw the circuit
5Ω
15Ω
+
V2
_
I1
I2
Ix
S
V
I
Y
II
IV
x
x
15
4
(4)(3)sub
)4.......(
20
5
)3.......(15
2
2
22
2
2




S
V
I
Y
IV
5
1
5
2
1
12
12



14. Thank
You