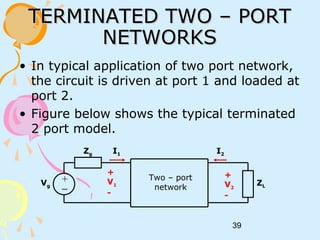
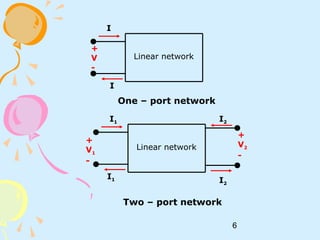
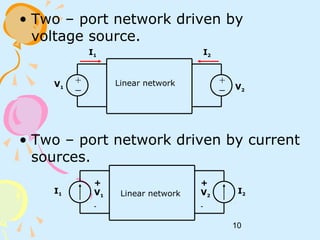
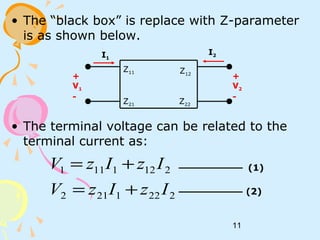
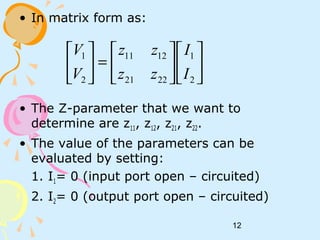
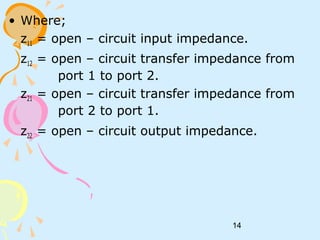
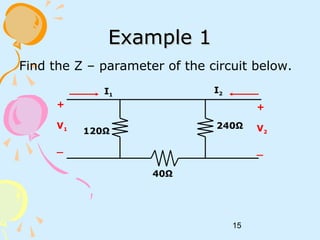
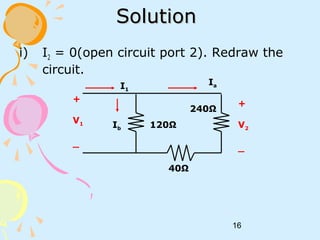
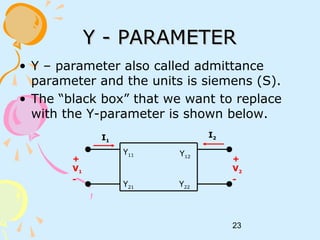
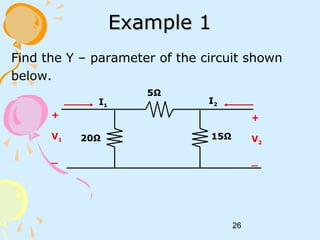
This document discusses two-port networks and their parameters. It defines a two-port network as having two ports for input and output, with four variables - I1, I2, V1, V2. The parameters that relate these variables are Z (impedance), Y (admittance), and T (ABCD transmission). It provides examples of calculating the parameters for given circuits by opening or closing ports. The objectives are to understand two-port networks and analyze their behavior using different parameter representations.

1. 1
TWO PORTTWO PORT
NETWORKSNETWORKS

2. 2
SUB - TOPICSSUB - TOPICS
Z – PARAMETER
Y – PARAMETER
T (ABCD) – PARAMETER
TERMINATED TWO PORT NETWORKS

3. 3
OBJECTIVESOBJECTIVES
• TO UNDERSTAND ABOUT TWO – PORT
NETWORKS AND ITS FUNTIONS.
• TO UNDERSTAND THE DIFFERENT
BETWEEN Z – PARAMETER, Y –
PARAMETER, T – PARAMETER AND
TERMINATED TWO PORT NETWORKS.
• TO INVERTIGATE AND ANALYSIS THE
BEHAVIOUR OF TWO – PORT NETWORKS.

4. 4
TWO – PORT NETWORKSTWO – PORT NETWORKS
• A pair of terminals through which a
current may enter or leave a network is
known as a port.
• Two terminal devices or elements (such as
resistors, capacitors, and inductors)
results in one – port network.
• Most of the circuits we have dealt with so
far are two – terminal or one – port
circuits.

5. 5
• A two – port network is an electrical
network with two separate ports for
input and output.
• It has two terminal pairs acting as
access points. The current entering
one terminal of a pair leaves the
other terminal in the pair.

6. 6
Linear network
+
V
-
I
I
One – port network
Linear network
+
V1
-
I1
I1 I2
I2
+
V2
-
Two – port network

7. 7
• Two (2) reason why to study two port –
network:
Such networks are useful in
communication, control system, power
systems and electronics.
Knowing the parameters of a two – port
network enables us to treat it as a
“black box” when embedded within a
larger network.

8. 8
• From the network, we can observe that
there are 4 variables that is I1, I2, V1and V2,
which two are independent.
• The various term that relate these
voltages and currents are called
parameters.

9. 9
Z – PARAMETERZ – PARAMETER
• Z – parameter also called as impedance
parameter and the units is ohm (Ω)
• Impedance parameters is commonly used
in the synthesis of filters and also useful in
the design and analysis of impedance
matching networks and power distribution
networks.
• The two – port network may be voltage –
driven or current – driven.

10. 10
• Two – port network driven by
voltage source.
• Two – port network driven by current
sources.
Linear network
I1 I2
+
−
+
−
V1 V2
I1 I2
+
V1
-
Linear network
+
V2
-

11. 11
• The “black box” is replace with Z-parameter
is as shown below.
• The terminal voltage can be related to the
terminal current as:
+
V1
-
I1
I2
+
V2
-
Z11
Z21
Z12
Z22
2221212
2121111
IzIzV
IzIzV
+=
+= (1)
(2)

12. 12
• In matrix form as:
• The Z-parameter that we want to
determine are z11, z12, z21, z22.
• The value of the parameters can be
evaluated by setting:
1. I1= 0 (input port open – circuited)
2. I2= 0 (output port open – circuited)












=





2
1
2221
1211
2
1
I
I
zz
zz
V
V

13. 13
• Thus,
01
2
21
01
1
11
2
2
=
=
=
=
I
I
I
V
z
I
V
z
02
2
22
02
1
12
1
1
=
=
=
=
I
I
I
V
z
I
V
z

14. 14
• Where;
z11 = open – circuit input impedance.
z12 = open – circuit transfer impedance from
port 1 to port 2.
z21 = open – circuit transfer impedance from
port 2 to port 1.
z22 = open – circuit output impedance.

15. 15
Example 1Example 1
Find the Z – parameter of the circuit below.
40Ω
240Ω
120Ω
+
V1
_
+
V2
_
I1
I2

16. 16
SolutionSolution
i) I2 = 0(open circuit port 2). Redraw the
circuit.
40Ω
240Ω
120Ω
+
V1
_
+
V2
_
I1
Ia
Ib

17. 17
Ω==∴
→
=
=
84
(2)(1)sub
)2......(
400
280
)1.......(120
1
1
11
1
1
I
V
Z
II
IV
b
b
Ω==∴
→
=
=
72
(3)(4)sub
)4.......(
400
120
.......(3)240
1
2
21
1
2
I
V
Z
II
IV
a
a

18. 18
ii) I1 = 0 (open circuit port 1). Redraw the
circuit.
40Ω
240Ω
120Ω
+
V1
_
+
V2
_
Iy I2
Ix

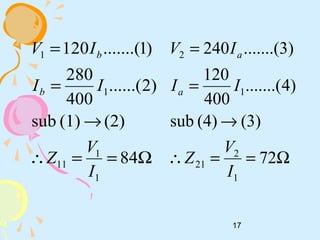
19. 19
Ω==∴
→
=
=
96Z
(2)(1)sub
)2.......(
400
160
)1.......(240
2
2
22
2
2
I
V
II
IV
x
x
Ω==∴
→
=
=
72
(3)(4)sub
)4.......(
400
240
)3.......(120
2
1
12
2
1
I
V
Z
II
IV
y
y
[ ] 





=
9672
7284
Z
In matrix form:

20. 20
Example 2Example 2
Find the Z – parameter of the circuit below
+
_
+
V1
_
+
V2
_-j20Ω
10Ωj4Ω2Ω
10I2
I2I1

21. 21
SolutionSolution
i) I2 = 0 (open circuit port 2). Redraw the circuit.
Ω=∴
=
Ω+==∴
+=
0Z
circuit)(short0V
j4)(2
I
V
Z
j4)(2IV
21
2
1
1
11
11
+
V1
_
j4Ω2ΩI1
+
V2
_
I2 = 0

22. 22
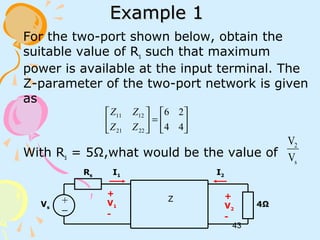
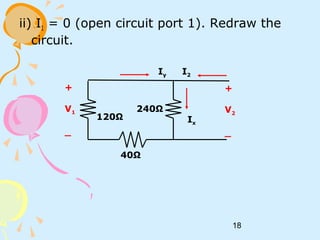
ii) I1 = 0 (open circuit port 1). Redraw the circuit.
Ω==∴






+=
+
−
=
Ω==∴
=
j8)-(16
I
V
Z
10
1
20
j
V2I
10
10I-V
j20
V
I
10
I
V
Z
10IV
2
2
22
22
222
2
2
1
12
21
[ ] 




 +
=
j8)-(1610
0j4)(2
Z
form;matrixIn
+
_
+
V1
_
+
V2
_-j20Ω
10Ω
10I2
I2I1 = 0

23. 23
Y - PARAMETERY - PARAMETER
• Y – parameter also called admittance
parameter and the units is siemens (S).
• The “black box” that we want to replace
with the Y-parameter is shown below.
+
V1
-
I1
I2
+
V2
-
Y11
Y21
Y12
Y22

24. 24
• The terminal current can be expressed in
term of terminal voltage as:
• In matrix form:
2221212
2121111
VyVyI
VyVyI
+=
+= (1)
(2)












=





2
1
2221
1211
2
1
V
V
yy
yy
I
I

25. 25
• The y-parameter that we want to determine
are Y11, Y12, Y21, Y22. The values of the
parameters can be evaluate by setting:
i) V1 = 0 (input port short – circuited).
ii) V2 = 0 (output port short – circuited).
• Thus;
01
2
21
01
1
11
2
2
=
=
=
=
V
V
V
I
Y
V
I
Y
02
2
22
02
1
12
1
1
=
=
=
=
V
V
V
I
Y
V
I
Y

26. 26
Example 1Example 1
Find the Y – parameter of the circuit shown
below.
5Ω
15Ω20Ω
+
V1
_
+
V2
_
I1
I2

27. 27
SolutionSolution
i) V2 = 0
5Ω
20Ω
+
V1
_
I1
I2
Ia
S
V
I
Y
II
IV
a
a
4
1
(2)(1)sub
)2.......(
25
5
)1.......(20
1
1
11
1
1
==∴
→
=
=
S
V
I
Y
IV
5
1
5
1
2
21
21
−==∴
−=

28. 28
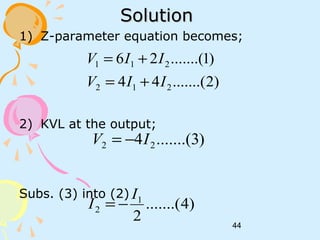
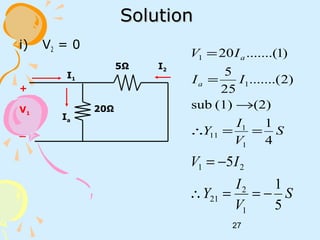
ii) V1 = 0
In matrix form;
5Ω
15Ω
+
V2
_
I1
I2
Ix
S
V
I
Y
II
IV
x
x
15
4
(4)(3)sub
)4.......(
25
5
)3.......(15
2
2
22
2
2
==∴
→
=
=
S
V
I
Y
IV
5
1
5
2
1
12
12
−==∴
−=
[ ] SY










−
−
=
15
4
5
1
5
1
4
1

29. 29
Example 2 (circuit withExample 2 (circuit with
dependent source)dependent source)
Find the Y – parameters of the circuit
shown.
+
_
+
V1
_
+
V2
_-j20Ω
10Ωj4Ω2Ω
10I2
I2I1

30. 30
SolutionSolution
i) V2 = 0 (short – circuit port 2). Redraw the circuit.
+
_
+
V1
_
10Ωj4Ω2Ω
10I2
I2
I1
S0
V
I
Y
Sj0.2)-(0.1
j42
1
V
I
Y
j4)I(2V
0I
1
2
21
1
1
11
11
==∴
=
+
==∴
+=
=

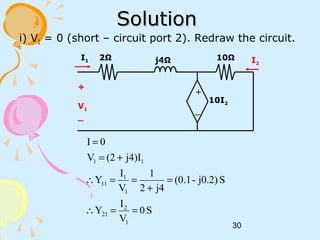
31. 31
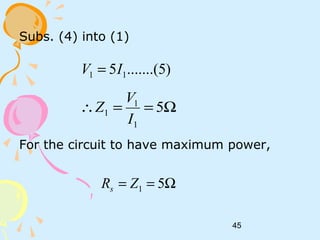
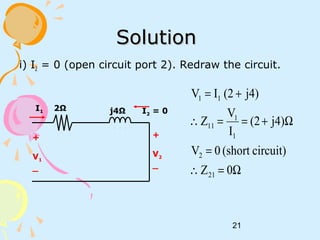
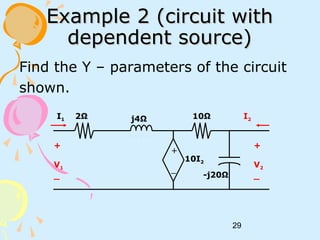
ii) V1 = 0 (short – circuit port 1). Redraw the circuit.
)2.......(
j20-
1
10
1
V2I
10
10I-V
j20-
V
I
)........(1
j42
10I-
I
22
222
2
2
1






+=
+=
+
=
+
_
+
V2
_-j20Ω
10Ωj4Ω2Ω
10I2
I2I1
[ ] S
j0.0250.050
j0.0751.0j0.20.1
Y
form;matrixIn
Sj0.075)(-0.1
V
I
Y
(1)(2)sub
Sj0.025)(0.05
V
I
Y
2
1
12
2
2
22






+
+−+
=∴
+==
→
+==∴

32. 32
T (ABCD) PARAMETERT (ABCD) PARAMETER
• T – parameter or ABCD – parameter is a
another set of parameters relates the
variables at the input port to those at the
output port.
• T – parameter also called transmission
parameters because this parameter are
useful in the analysis of transmission lines
because they express sending – end
variables (V1 and I1) in terms of the
receiving – end variables (V2 and -I2).

33. 33
• The “black box” that we want to replace with T –
parameter is as shown below.
• The equation is:
+
V1
-
I1
I2
+
V2
-
A11
C21
B12
D22
)2.......(
)1.......(
221
221
DICVI
BIAVV
−=
−=

34. 34
• In matrix form is:
• The T – parameter that we want
determine are A, B, C and D where A and
D are dimensionless, B is in ohm (Ω) and
C is in siemens (S).
• The values can be evaluated by setting
i) I2 = 0 (input port open – circuit)
ii) V2 = 0 (output port short circuit)






−





=





2
2
1
1
I
V
DC
BA
I
V

35. 35
• Thus;
• In term of the transmission parameter, a
network is reciprocal if;
02
1
02
1
2
2
=
=
=
=
I
I
V
I
C
V
V
A
02
1
02
1
2
2
=
=
=
=
V
V
I
I
D
I
V
B
1BC-AD =

36. 36
ExampleExample
Find the ABCD – parameter of the circuit
shown below.
2Ω
10Ω
+
V2
_
I1 I2
+
V1
_
4Ω

37. 37
SolutionSolution
i) I2 = 0,
2Ω
10Ω
+
V2
_
I1
+
V1
_
2.1
5
6
10
2
2
1.0
10
2
1
22
2
1
211
2
1
12
==∴
=+





=
+=
==∴
=
V
V
A
VV
V
V
VIV
S
V
I
C
IV

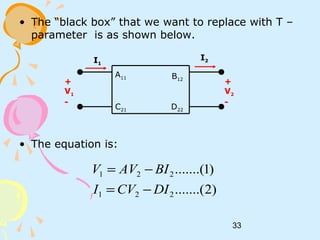
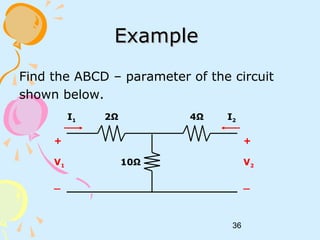
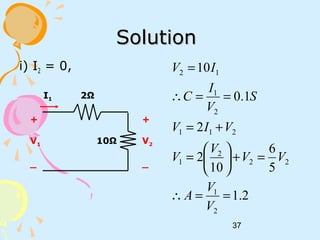
38. 38
ii) V2 = 0,
( )
Ω=−=∴
+





−=
+=
++=
=−=∴
−=
8.6
10
10
14
12
1012
102
4.1
14
10
2
1
221
211
2111
2
1
12
I
V
B
IIV
IIV
IIIV
I
I
D
II
2Ω
10Ω
I1 I2
+
V1
_
4Ω
I1 + I2
[ ] 





=
4.11.0
8.62.1
T

39. 39
TERMINATED TWO – PORTTERMINATED TWO – PORT
NETWORKSNETWORKS
• In typical application of two port network,
the circuit is driven at port 1 and loaded at
port 2.
• Figure below shows the typical terminated
2 port model.
+
V1
-
I1 I2
+
V2
-
+
−
Zg
ZLVg
Two – port
network

40. 40
• Zg represents the internal impedance of
the source and Vg is the internal voltage of
the source and ZL is the load impedance.
• There are a few characteristics of the
terminated two-port network and some of
them are;
gV
V
V
V
I
I
I
V
I
V
2
g
1
2
v
1
2
i
2
2
o
1
1
i
Again,voltageoverallv)
Again,voltageiv)
Again,currentiii)
Zimpedance,outputii)
Zimpedance,inputi)
=
=
=
=
=

41. 41
• The derivation of any one of the desired
expression involves the algebraic
manipulation of the two – port equation. The
equation are:
1) the two-port parameter equation either Z
or Y or ABCD.
For example, Z-parameter,
)2.......(IZIZV
)1.......(IZIV
2221212
2121111
+=
+= Z

42. 42
2) KVL at input,
3) KVL at the output,
• From these equations, all the characteristic
can be obtained.
.......(3)ZIVV g1g1 −=
)4.......(ZIV L22 −=

43. 43
Example 1Example 1
For the two-port shown below, obtain the
suitable value of Rs such that maximum
power is available at the input terminal. The
Z-parameter of the two-port network is given
as
With Rs = 5Ω,what would be the value of






=





44
26
2221
1211
ZZ
ZZ
s
2
V
V
+
V1
-
I1 I2
+
V2
-
+
−
Rs
4ΩVs
Z

44. 44
SolutionSolution
1) Z-parameter equation becomes;
2) KVL at the output;
Subs. (3) into (2)
)2.......(44
)1.......(26
212
211
IIV
IIV
+=
+=
)3.......(4 22 IV −=
)4.......(
2
1
2
I
I −=

45. 45
Subs. (4) into (1)
For the circuit to have maximum power,
)5.......(5 11 IV =
Ω==∴ 5
1
1
1
I
V
Z
Ω== 51ZRs

46. 46
To find at max. power transfer, voltage
drop at Z1 is half of Vs
From equations (3), (4), (5) & (6)
Overall voltage gain,
s
2
V
V
)6.......(
2
1
sV
V =
5
12
==
s
g
V
V
A

47. 47
Example 2Example 2
The ABCD parameter of two – port network shown
below are.
The output port is connected to a variable load for
a maximum power transfer. Find RL and the
maximum power transferred.





 Ω
20.1S
204

48. 48
ABCD parameter equation becomes
V1 = 4V2 – 20I2
I1 = 0.1V2 – 2I2
At the input port, V1 = -10I
(1)
(2)
(3)
Solution

49. 49
(3) Into (1)
-10I1 = 4V2 – 20I2
I1 = -0.4V2 2I2
(2) = (4)
0.1V2 – 2I2 = -0.4V2 + 2I2
0.5V2 = 4I2
From (5);
ZTH = V2/I2 = 8Ω
(4)
(5)
(6)

50. 50
But from Figure (b), we know that
V1 = 50 – 10I1 and I2 =0
Sub. these into (1) and (2)
50 – 10I1 = 4V2
I1 = 0.1V2
(8)
(7)

51. 51
Sub (8) into (7)
V2 = 10
Thus, VTH = V2 = 10V
RL for maximum power transfer,
RL = ZTH = 8Ω
The maximum power
P = I2
RL = (VTH/2RL)2
x RL = V2
TH/4RL = 3.125W