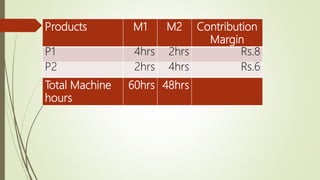
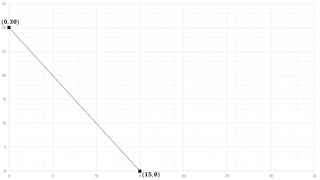
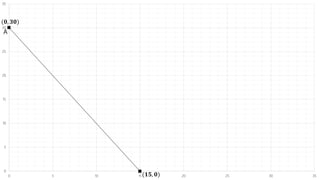
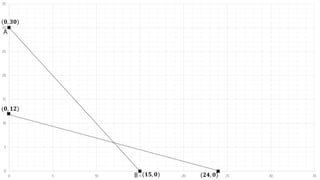
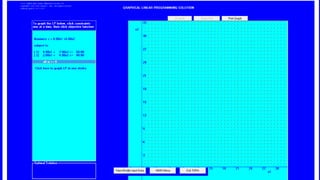
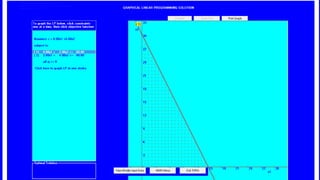
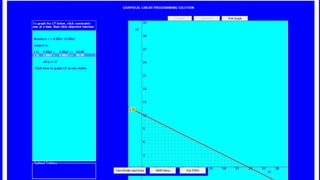
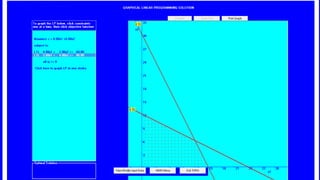
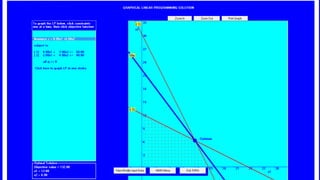
The document describes a production problem involving two products (P1 and P2) that are manufactured using two machines (M1 and M2). P1 requires 4 hours on M1 and 2 hours on M2, while P2 requires 2 hours on M1 and 4 hours on M2. The goal is to determine the optimal quantities of P1 and P2 to maximize total contribution, given 60 hours available on M1 and 48 hours on M2. This problem is modeled as a linear programming problem and graphically solved by plotting the constraint lines and finding their intersection point.

1. Graphical Method
LPP

2. Two products, namely P1 and P2 are being manufactured.
Each product has to be processed through two machines
M1 and M2. One unit of product P1 consumes 4 hours of
time on M1 and 2 hours of time on M2. Similarly, one unit
of P2 consumes 2 hours of time on M1 and 4 hours of
time on M2. 60 hours of time is available on M1 and 48
hours on M2. The per unit contribution margin of P1 is 8
and of P2 is 6. Determine the number of units of P1 and
P2 to be manufactured so as to maximise total
contribution.

3. Products M1 M2 Contribution
Margin
P1 4hrs 2hrs Rs.8
P2 2hrs 4hrs Rs.6
Total Machine
hours
60hrs 48hrs

4. 𝑻𝒉𝒆 𝒂𝒃𝒐𝒗𝒆 𝒑𝒓𝒐𝒃𝒍𝒆𝒎 𝒄𝒂𝒏 𝒃𝒆 𝒇𝒐𝒓𝒎𝒖𝒍𝒂𝒕𝒆𝒅 𝒂𝒔:
𝑴𝒂𝒙𝒊𝒎𝒊𝒔𝒆 𝒛 = 𝟖𝒙 𝟏 + 𝟔𝒙 𝟐
𝒔𝒖𝒃𝒋𝒆𝒄𝒕 𝒕𝒐 𝒕𝒉𝒆 𝒄𝒐𝒏𝒔𝒕𝒓𝒂𝒊𝒏𝒕𝒔:
𝟒𝒙 𝟏 + 𝟐𝒙 𝟐 ≤ 𝟔𝟎
𝟐𝒙 𝟏 + 𝟒𝒙 𝟐 ≤ 𝟒𝟖
𝒙 𝟏 ≥ 𝟎
𝒙 𝟐 ≥ 𝟎

5. 𝑷𝒍𝒐𝒕𝒕𝒊𝒏𝒈 𝒕𝒉𝒆 𝒕𝒘𝒐 𝒄𝒐𝒏𝒔𝒕𝒓𝒂𝒊𝒏𝒕𝒔, 𝒕𝒓𝒆𝒂𝒕𝒊𝒏𝒈 𝒕𝒉𝒆𝒎 𝒂𝒔 𝒔𝒕𝒓𝒊𝒄𝒕
𝒆𝒒𝒖𝒂𝒍𝒊𝒕𝒊𝒆𝒔:
𝟒𝒙 𝟏 + 𝟐𝒙 𝟐 ≤ 𝟔𝟎
𝒐𝒓 𝟒𝒙 𝟏 + 𝟐𝒙 𝟐 = 𝟔𝟎 … (𝒊)
𝟐𝒙 𝟏 + 𝟒𝒙 𝟐 ≤ 𝟒𝟖
𝒐𝒓 𝟐𝒙 𝟏 + 𝟒𝒙 𝟐 = 𝟒𝟖 … 𝒊𝒊

6. 𝑰𝒏 𝒆𝒒𝒖𝒂𝒕𝒊𝒐𝒏 𝒊 , 𝒍𝒆𝒕 𝒙 𝟏 = 𝟎
𝟒 × 𝟎 + 𝟐𝒙 𝟐 = 𝟔𝟎
𝒐𝒓 𝟎 + 𝟐𝒙 𝟐 = 𝟔𝟎
𝒐𝒓 𝟐𝒙 𝟐 = 𝟔𝟎
𝒃𝒚 𝒄𝒓𝒐𝒔𝒔 − 𝒎𝒖𝒍𝒕𝒊𝒑𝒍𝒊𝒄𝒂𝒕𝒊𝒐𝒏:
𝒙 𝟐 =
𝟔𝟎
𝟐
𝒐𝒓 𝒙 𝟐 = 𝟑𝟎
∴ 𝒕𝒉𝒆 𝒇𝒊𝒓𝒔𝒕 𝒑𝒐𝒊𝒏𝒕 𝒐𝒏 𝒍𝒊𝒏𝒆 𝒊 = (𝟎, 𝟑𝟎)

7. 𝑰𝒏 𝒆𝒒𝒖𝒂𝒕𝒊𝒐𝒏 𝒊 , 𝒍𝒆𝒕 𝒙 𝟐 = 𝟎
𝟒𝒙 𝟏 + 𝟐 × 𝟎 = 𝟔𝟎
𝒐𝒓 𝟒𝒙 𝟏 + 𝟎 = 𝟔𝟎
𝒐𝒓 𝟒𝒙 𝟏 = 𝟔𝟎
𝒃𝒚 𝒄𝒓𝒐𝒔𝒔 − 𝒎𝒖𝒍𝒕𝒊𝒑𝒍𝒊𝒄𝒂𝒕𝒊𝒐𝒏:
𝒙 𝟏 =
𝟔𝟎
𝟒
𝒐𝒓 𝒙 𝟏 = 𝟏𝟓
∴ 𝒕𝒉𝒆 𝒔𝒆𝒄𝒐𝒏𝒅 𝒑𝒐𝒊𝒏𝒕 𝒐𝒏 𝒍𝒊𝒏𝒆 𝒊 = (𝟏𝟓, 𝟎)

8. 𝑰𝒏 𝒆𝒒𝒖𝒂𝒕𝒊𝒐𝒏 𝒊𝒊 , 𝒍𝒆𝒕 𝒙 𝟏 = 𝟎
𝟐 × 𝟎 + 𝟒𝒙 𝟐 = 𝟒𝟖
𝒐𝒓 𝟎 + 𝟒𝒙 𝟐 = 𝟒𝟖
𝒐𝒓 𝟒𝒙 𝟐 = 𝟒𝟖
𝒃𝒚 𝒄𝒓𝒐𝒔𝒔 − 𝒎𝒖𝒍𝒕𝒊𝒑𝒍𝒊𝒄𝒂𝒕𝒊𝒐𝒏:
𝒙 𝟐 =
𝟒𝟖
𝟒
𝒐𝒓 𝒙 𝟐 = 𝟏𝟐
∴ 𝒕𝒉𝒆 𝒇𝒊𝒓𝒔𝒕 𝒑𝒐𝒊𝒏𝒕 𝒐𝒏 𝒍𝒊𝒏𝒆 𝒊𝒊 = (𝟎, 𝟏𝟐)

9. 𝑰𝒏 𝒆𝒒𝒖𝒂𝒕𝒊𝒐𝒏 𝒊𝒊 , 𝒍𝒆𝒕 𝒙 𝟐 = 𝟎
𝟐𝒙 𝟏 + 𝟒 × 𝟎 = 𝟒𝟖
𝒐𝒓 𝟐𝒙 𝟏 + 𝟎 = 𝟒𝟖
𝒐𝒓 𝟐𝒙 𝟏 = 𝟒𝟖
𝒃𝒚 𝒄𝒓𝒐𝒔𝒔 − 𝒎𝒖𝒍𝒕𝒊𝒑𝒍𝒊𝒄𝒂𝒕𝒊𝒐𝒏:
𝒙 𝟏 =
𝟒𝟖
𝟐
𝒐𝒓 𝒙 𝟏 = 𝟐𝟒
∴ 𝒕𝒉𝒆 𝒔𝒆𝒄𝒐𝒏𝒅 𝒑𝒐𝒊𝒏𝒕 𝒐𝒏 𝒍𝒊𝒏𝒆 𝒊𝒊 = 𝟐𝟒, 𝟎
𝑷𝒍𝒐𝒕𝒕𝒊𝒏𝒈 𝒕𝒉𝒆 𝒕𝒘𝒐 𝒍𝒊𝒏𝒆𝒔:

10. 0
5
10
15
20
25
30
35
0 5 10 15 20 25 30 35

11. 0
5
10
15
20
25
30
35
0 5 10 15 20 25 30 35

12. 0
5
10
15
20
25
30
35
0 5 10 15 20 25 30 35
(𝟎, 𝟑𝟎)

13. 0
5
10
15
20
25
30
35
0 5 10 15 20 25 30 35
(𝟎, 𝟑𝟎)

14. 0
5
10
15
20
25
30
35
0 5 10 15 20 25 30 35
(𝟎, 𝟑𝟎)
(𝟏𝟓, 𝟎)

15. 0
5
10
15
20
25
30
35
0 5 10 15 20 25 30 35
(𝟎, 𝟑𝟎)
(𝟏𝟓, 𝟎)

16. 0
5
10
15
20
25
30
35
0 5 10 15 20 25 30 35
(𝟎, 𝟑𝟎)
(𝟏𝟓, 𝟎)
A

17. 0
5
10
15
20
25
30
35
0 5 10 15 20 25 30 35
(𝟎, 𝟑𝟎)
(𝟏𝟓, 𝟎)
A
B

18. 0
5
10
15
20
25
30
35
0 5 10 15 20 25 30 35
(𝟎, 𝟑𝟎)
(𝟏𝟓, 𝟎)
A
B

19. 0
5
10
15
20
25
30
35
0 5 10 15 20 25 30 35
(𝟎, 𝟑𝟎)
(𝟏𝟓, 𝟎)
A
B
(𝟎, 𝟏𝟐)

20. 0
5
10
15
20
25
30
35
0 5 10 15 20 25 30 35
(𝟎, 𝟑𝟎)
(𝟏𝟓, 𝟎)
A
B
(𝟎, 𝟏𝟐)

21. 0
5
10
15
20
25
30
35
0 5 10 15 20 25 30 35
(𝟎, 𝟑𝟎)
(𝟏𝟓, 𝟎)
A
B
(𝟎, 𝟏𝟐)
(𝟐𝟒, 𝟎)

22. 0
5
10
15
20
25
30
35
0 5 10 15 20 25 30 35
(𝟎, 𝟑𝟎)
(𝟏𝟓, 𝟎)
A
B
(𝟎, 𝟏𝟐)
(𝟐𝟒, 𝟎)
C

23. 0
5
10
15
20
25
30
35
0 5 10 15 20 25 30 35
(𝟎, 𝟑𝟎)
(𝟏𝟓, 𝟎)
A
B
(𝟎, 𝟏𝟐)
(𝟐𝟒, 𝟎)
C