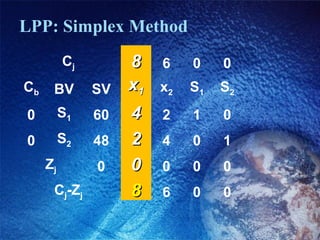
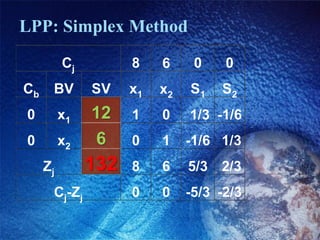
Operations research (OR) is a tool used to increase the effectiveness of managerial decisions. It can help with profit maximization, production management like determining optimal product mix and scheduling, financial management, marketing management, and personnel management. Some common OR models include linear programming, transportation, assignment, and sequencing problems. OR uses mathematical techniques like linear programming, decision theory, game theory, queuing theory, simulation, network analysis, and inventory models.

1. Operations Research
Dr. Anurag Srivastava

2. Definition
• Operations Research is a tool employed
to increase the effectiveness of
managerial decisions as an objective
supplement to the subjective feeling of the
decision-maker.

3. Business Application
• Profit Maximisation. Under the existing
constraints, to utilise the resources in the
best possible way so as to maximise the
profits.

4. Business Application
Production Management
• To calculate the optimum product mix.
• For scheduling and sequencing the
production runs by proper allocation of
machines. (The Transportation model may
be applied in order to determine the
optimum production schedule.)

5. Business Application
Financial Management
• To decide the optimum mix of equity and
debt.
• Every capital has a cost associated with it,
including owner’s capital, which is opportunity
cost. This cost, as well as the risk on
borrowed capital has to be minimised. OR
helps in doing this.
• The financial manager not only mobilises
funds, he also has to utilise the funds, in
which OR assists him.

6. Business Application
Marketing Management
• Sales can be promoted by improving quality
or reducing cost, intensive or extensive
advertising. OR assists in the optimal
allocation of budget on these different
methods.
• OR is also useful in the prediction of the
market share of a particular firm. For this,
past experience is made use of. The matrix of
transitive probabilities is used for the
purpose.

7. Business Application
Personnel Management
OR is useful to the personnel administrator
in finding out:
• skilled personnel at the minimum cost;
• the number of persons to be maintained
on the full time basis in a variable
workload, like freight, etc., and
• the optimum manner of sequencing
personnel to a variety of jobs.

8. Mathematical Models
• A mathematical model in OR is described
in terms of two important variables –
parameters (uncontrollable) and decision
(controllable) variables.
• We cantake a decision regarding decision
variables only.

9. OR Mathematical Models
• Linear Programming Model
• Transportation Model
• Assignment Model
• Sequencing Problem
• Decision Theory
• Game Theory
• Queuing Theory
• Simulation Model
• Network Analysis
• Replacement Decisions
• Inventory Models

10. Linear Programming Model
• Programming, in American parlance is
another name for planning. In linear
programming we study about planning
and allocation of resources.
• In linear programming we are concerned
with the definition of economics as given
by Lionel Robbins:
“Economics is the science which studies
human behaviour as a relationship between
ends and scarce means which have
alternative uses.”

11. Linear Programming Model
• ‘Ends’ are the objectives to be achieved
and resources are to be allocated such as
to achieve the objectives.
• The ‘means’ to achieve the objectives, that
is, the resources have alternative
applications.
• Every resource generates a separate
constraint. These constraints can be
expressed as linear equations or
inequalities. This gives us an LPP.

12. Linear Programming Model
Two products, namely, P1 and P2 are being
manufactured. Each product has to be
processed through two machines M1 and M2.
One unit of product P1 consumes 4 hours of
time on M1 and 2 hours of time on M2.
Similarly, one unit of P2 consumes 2 hours of
time on M1 and 4 hours of time on M2. 60
hours of time is available on M1 and 48 hours
on M2. The per unit contribution margin of P1 is
8 and of P2 is 6. Determine the number of units
of P1 and P2 to be manufactured so as to
maximise total contribution.

13. Linear Programming Model
Maximise:
z = 8x1 + 6x2
subject to the constraints:
4x1 + 2x2 ≤ 60
2x1 + 4x2 ≤ 48
x1 ≥ 0
x2 ≥ 0

14. LPP: Graphical Method
• Extreme Point Theorem. The optimum
solution to a linear programming problem
lies at one of the extremities of the
feasible polygon, provided there exists a
solution to the linear programming
problem which is unique, finite and
optimal.

15. LPP: Trial and Error Method
• Basis Theorem. If in a system of n
equations in m variables, m > n, then a
solution obtained by keeping m - n of the
variables as zero results in a corner point
and is known as a basic solution.

16. LPP: Algebraic Method

17. LPP: Simplex Method
x1 x2

18. LPP: Simplex Method
x1 x2 S1 S2

19. LPP: Simplex Method
Cb BV SV x1 x2 S1 S2

20. LPP: Simplex Method
Cj 8 6 0 0
Cb BV SV x1 x2 S1 S2

21. LPP: Simplex Method
Cj 8 6 0 0
Cb BV SV x1 x2 S1 S2
S1
S2

22. LPP: Simplex Method
Cj 8 6 0 0
Cb BV SV x1 x2 S1 S2
0 S1
0 S2

23. LPP: Simplex Method
Cj 8 6 0 0
Cb BV SV x1 x2 S1 S2
0 S1 60 4 2 1 0
0 S2 48 2 4 0 1

24. LPP: Simplex Method
Cj 8 6 0 0
Cb BV SV x1 x2 S1 S2
0 S1 60 4 2 1 0
0 S2 48 2 4 0 1
Zj

25. LPP: Simplex Method
Cj 8 6 0 0
Cb BV SV x1 x2 S1 S2
0 S1 60 4 2 1 0
0 S2 48 2 4 0 1
Zj 0 0 0 0 0

26. LPP: Simplex Method
Cj 8 6 0 0
Cb BV SV x1 x2 S1 S2
0 S1 60 4 2 1 0
0 S2 48 2 4 0 1
Zj 0 0 0 0 0
Cj-Zj

27. LPP: Simplex Method
Cj 8 6 0 0
Cb BV SV x1 x2 S1 S2
0 S1 60 4 2 1 0
0 S2 48 2 4 0 1
Zj 0 0 0 0 0
Cj-Zj 8 6 0 0

28. LPP: Simplex Method
Cj 8 6 0 0
Cb BV SV x1 x2 S1 S2
0 S1 60 4 2 1 0
0 S2 48 2 4 0 1
Zj 0 0 0 0 0
Cj-Zj 88 6 0 0

29. LPP: Simplex Method
Cj 88 6 0 0
Cb BV SV xx11 x2 S1 S2
0 S1 60 44 2 1 0
0 S2 48 22 4 0 1
Zj 0 00 0 0 0
Cj-Zj 88 6 0 0

30. LPP: Simplex Method
Cj 88 6 0 0
Cb BV SV xx11 x2 S1 S2
0 S1 60 44 2 1 0 15
0 S2 48 22 4 0 1 24
Zj 0 00 0 0 0
Cj-Zj 88 6 0 0

31. LPP: Simplex Method
Cj 88 6 0 0
Cb BV SV xx11 x2 S1 S2
00 SS11 6060 44 22 11 00 15
0 S2 48 22 4 0 1 24
Zj 0 00 0 0 0
Cj-Zj 88 6 0 0

32. LPP: Simplex Method
Cj 8 6 0 0
Cb BV SV x1 x2 S1 S2
0 x1 15 1 ½ ¼ 0 R1=R1/4
0 S2

33. LPP: Simplex Method
Cj 8 6 0 0
Cb BV SV x1 x2 S1 S2
0 x1 15 1 ½ ¼ 0 R1=R1/4
0 S2 18 0 3 -½ 1 R2=R2-2R1

34. LPP: Simplex Method
Cj 8 6 0 0
Cb BV SV x1 x2 S1 S2
0 x1 15 1 ½ ¼ 0
0 S2 18 0 3 -½ 1
Zj 120 8 4 2 0

35. LPP: Simplex Method
Cj 8 6 0 0
Cb BV SV x1 x2 S1 S2
0 x1 15 1 ½ ¼ 0
0 S2 18 0 3 -½ 1
Zj 120 8 4 2 0
Cj-Zj 0 2 -2 0

36. LPP: Simplex Method
Cj 8 6 0 0
Cb BV SV x1 x2 S1 S2
0 x1 15 1 ½ ¼ 0
0 S2 18 0 3 -½ 1
Zj 120 8 4 2 0
Cj-Zj 0 22 -2 0

37. LPP: Simplex Method
Cj 8 66 0 0
Cb BV SV x1 xx22 S1 S2
0 x1 15 1 ½½ ¼ 0
0 S2 18 0 33 -½ 1
Zj 120 8 44 2 0
Cj-Zj 0 22 -2 0

38. LPP: Simplex Method
Cj 8 66 0 0
Cb BV SV x1 xx22 S1 S2
0 x1 15 1 ½½ ¼ 0 30
00 SS22 1818 00 33 -½-½ 11 6
Zj 120 8 44 2 0
Cj-Zj 0 22 -2 0

39. LPP: Simplex Method
Cj 8 6 0 0
Cb BV SV x1 x2 S1 S2
0 x1
0 x2 6 0 1 -1/6 1/3 R2=R2/3
Zj
Cj-Zj

40. LPP: Simplex Method
Cj 8 6 0 0
Cb BV SV x1 x2 S1 S2
0 x1 12 1 0 1/3 -1/6 R1=R1-½R2
0 x2 6 0 1 -1/6 1/3 R2=R2/3
Zj
Cj-Zj

41. LPP: Simplex Method
Cj 8 6 0 0
Cb BV SV x1 x2 S1 S2
0 x1 12 1 0 1/3 -1/6
0 x2 6 0 1 -1/6 1/3
Zj 132 8 6 5/3 2/3
Cj-Zj

42. LPP: Simplex Method
Cj 8 6 0 0
Cb BV SV x1 x2 S1 S2
0 x1 12 1 0 1/3 -1/6
0 x2 6 0 1 -1/6 1/3
Zj 132 8 6 5/3 2/3
Cj-Zj 0 0 -5/3 -2/3

43. LPP: Simplex Method

44. Linear Programming Model
Types of Variables:Types of Variables:
• Slack variables; S1, S2, S3, etc.
• Surplus variables; S1, S2, S3, etc.
• Artificial variables; A1, A2, A3, etc.
• Structural variables; x1, x2, x3, etc.
• Non-structural variables; S1, S2, S3, etc. and
A1, A2, A3, etc.
• Basic variables;
• Non-basic variables.

45. Linear Programming Model
Special Cases in LPPSpecial Cases in LPP::
• Infeasible solution
• Multiple optimal solution
• Redundancy
• Unbounded solution

46. Transportation Model
• The transportation problem deals with the
transportation of a product manufactured
at different plants or factories (supply
origins) to a number of different
warehouses (demand destinations) with
the objective to satisfy the destination
requirements within the plant capacity
constraints at the minimum transportation
cost.

47. Assignment Model
• The assignment problem refers to another
special class of LPP where the objective is
to assign a number of resources (items) to
an equal number of activities (receivers)
on a one to one basis so as to minimise
the total cost (or total time) of performing
the tasks at hand or maximise the total
profit from allocation.

48. Sequencing Problem
• Sequencing problems are concerned with
an appropriate selection of a sequence of
jobs to be done on a finite number of
service facilities (like machines) in some
well-defined technological order so as to
optimise some efficiency measure such as
total elapsed time or overall cost, etc.

49. Decision Theory

50. Game Theory

51. Queuing Theory
• The study of waiting lines, called ‘queuing
theory,’ is one of the oldest and most
widely used OR techniques.

52. Simulation Model

53. Network Analysis

54. Replacement Decisions
• Replacement theory is concerned with the
problem of replacement of machines,
electricity bulbs, men, etc., due to their
deteriorating efficiency, failure or
breakdown.

55. Inventory Models