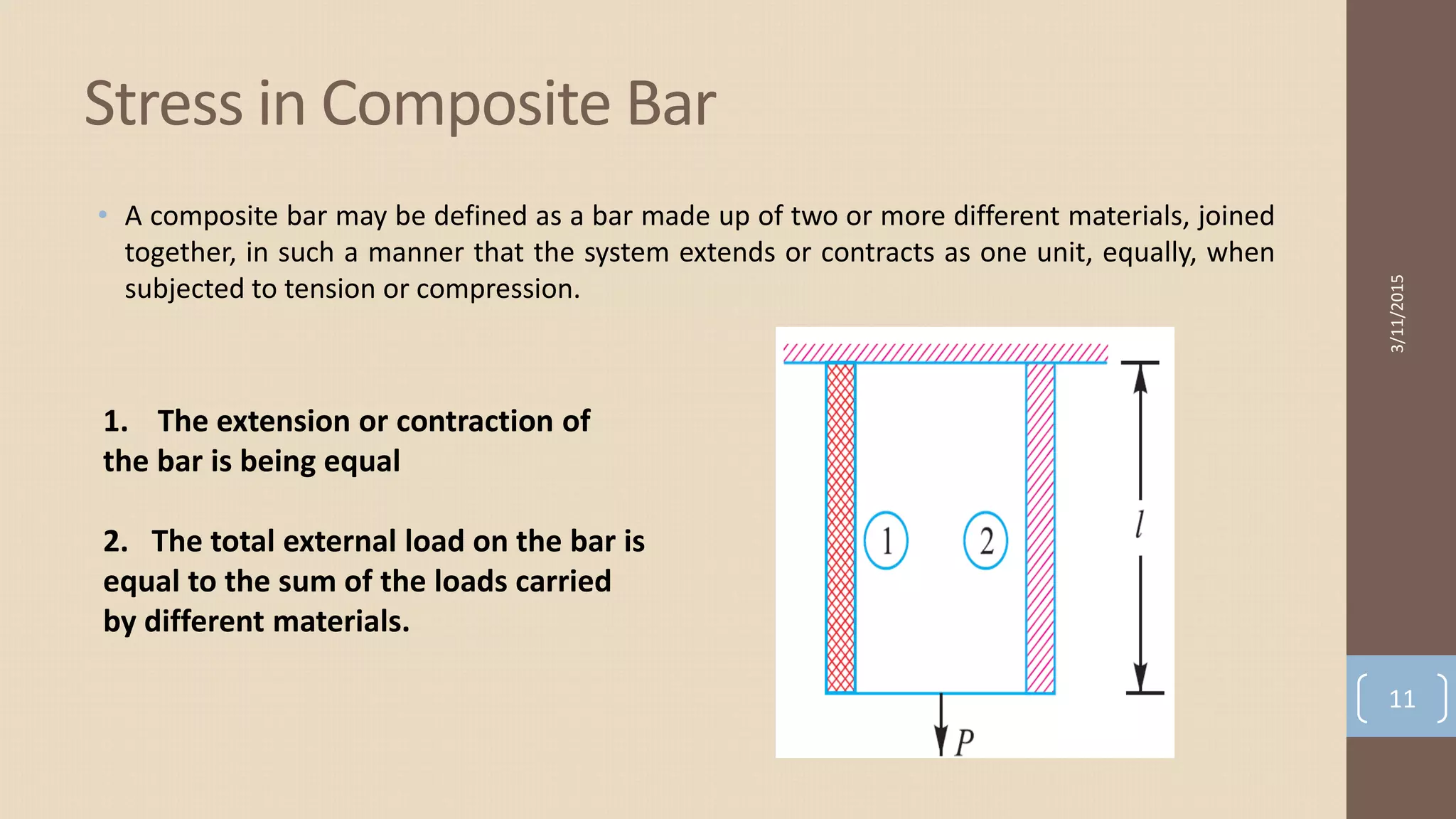
The document provides an overview of stress and strain in solid mechanics, detailing various types of stress including tensile, compressive, and shear stress, as well as their corresponding strains. It discusses Young's modulus, Hooke's law, and the concept of thermal stresses, including the effects of temperature changes on materials. Additionally, it introduces composite bars, linear and lateral strain, Poisson's ratio, volumetric strain, and bulk modulus.

1. Mechanics of solid
Stress and Strain
By Kaushal Patel

2. • 𝜎 = 𝐹/𝐴
Stress
3/11/2015
2

3. • 𝜀 = 𝛿𝑙/𝐿
Strain
h
l
3/11/2015
3

4. • When a body is subjected to two equal and opposite axial pulls P (also called
tensile load) , then the stress induced at any section of the body is known as
tensile stress.
• Tensile load, there will be a decrease in cross-sectional area and an increase
in length of the body. The ratio of the increase in length to the original length
is known as tensile strain.
Tensile Stress and Strain
3/11/2015
4

5. • When a body is subjected to two equal and opposite axial pushes P (also
called compressive load) , then the stress induced at any section of the body
is known as compressive stress
• Compressive load, there will be an increase in cross-sectional area and a
decrease in length of the body. The ratio of the decrease in length to the
original length Is known as compressive strain
Compressive Stress and Strain
3/11/2015
5

6. 3/11/2015
6

7. Young’s Modulus or Modulus of Elasticity
• Hooke's law:- states that when a material is loaded within elastic limit, the stress is
directly proportional to strain,
σ ∝ ε or σ = E × ε
• 𝐸 =
𝜎
𝜀
=
𝑃.𝑙
𝐴.𝛿𝑙
3/11/2015
7

8. • When a body is subjected to two equal and opposite forces acting
tangentially across the resisting section, as a result of which the body tends to
shear off the section, then the stress induced is called shear stress (τ), The
corresponding strain is known as shear strain (φ)
• Shear stress, 𝜏 =
𝑇𝑎𝑛𝑔𝑒𝑛𝑡𝑖𝑎𝑙 𝑓𝑜𝑟𝑐𝑒
𝑅𝑒𝑠𝑖𝑠𝑡𝑖𝑛𝑔 𝑎𝑟𝑒𝑎
Shear Stress and Strain
3/11/2015
8

9. • It has been found experimentally that within the elastic limit, the shear stress
is directly proportional to shear strain.
Mathematically τ ∝ φ or τ = G . φ or τ / φ = G
• where, τ = Shear stress,
• φ = Shear strain,
• G = Constant of proportionality, known as shear modulus or modulus of
rigidity.
It is also denoted by N or C.
Shear Modulus or Modulus of Rigidity
3/11/2015
9

10. Stress-Stress Diagram
3/11/2015
10

11. • A composite bar may be defined as a bar made up of two or more different materials, joined
together, in such a manner that the system extends or contracts as one unit, equally, when
subjected to tension or compression.
Stress in Composite Bar
1. The extension or contraction of
the bar is being equal
2. The total external load on the bar is
equal to the sum of the loads carried
by different materials.
3/11/2015
11

12. • P1 = Load carried by bar 1,
• A1 = Cross-sectional area of bar 1,
• σ1 = Stress produced in bar 1,
• E1 = Young's modulus of bar 1,
• P2, A2, σ2, E2 = Corresponding values of bar 2,
• P = Total load on the composite bar,
• l = Length of the composite bar, and
• δl = Elongation of the composite bar.
• We know that P = P1 + P2
• Stress in bar 1, 𝜎1 =
𝑃1
𝐴1
• strain in bar 1, 𝜀 =
𝜎1
𝐸1
=
𝑃1
𝐴1 𝐸1
Continue…
3/11/2015
12

13. • Elongation in bar -1: 𝛿𝑙1 =
𝑃1 𝑙
𝐴1 𝐸1
• Elongation in bar -2: 𝛿𝑙2 =
𝑃2 𝑙
𝐴2 𝐸2
There fore,
δl1 = δl2
𝑃1 𝑙
𝐴1 𝐸1
=
𝑃2 𝑙
𝐴2 𝐸2
𝜎1
𝐸1
=
𝜎2
𝐸2
𝑃 = 𝑃1 + 𝑃2 = 𝜎1 𝐴1 + 𝜎2 𝐴2
• The ratio E1 / E2 is known as modular ratio of the two materials
Continue…
3/11/2015
13

14. • A typical bar with cross-sections varying in steps and subjected to axial load
• length of three portions L1, L2 and L3 and the respective cross-sectional areas
are A1, A2, A3
• E = Young’s modulus of the material
• P = applied axial load.
Bars with Cross Section Varying in Steps
3/11/2015
14

15. • Forces acting on the cross-sections of the three portions. It is obvious that to
maintain equilibrium the load acting on each portion is P only.
Continue…
3/11/2015
15

16. Stress Strain and Extension of each Bar
Portion Stress Strain Extension
1 σ1 = P/ A1 e1 = σ1 / E δ1 = P L1 / A1 E
2 σ2 = P/ A2 e2 = σ2 / E δ2 = P L2 / A2 E
3 σ3 = P/ A3 e3 = σ3 / E δ3 = P L3 / A3 E
3/11/2015
16

17. • Total elongation,
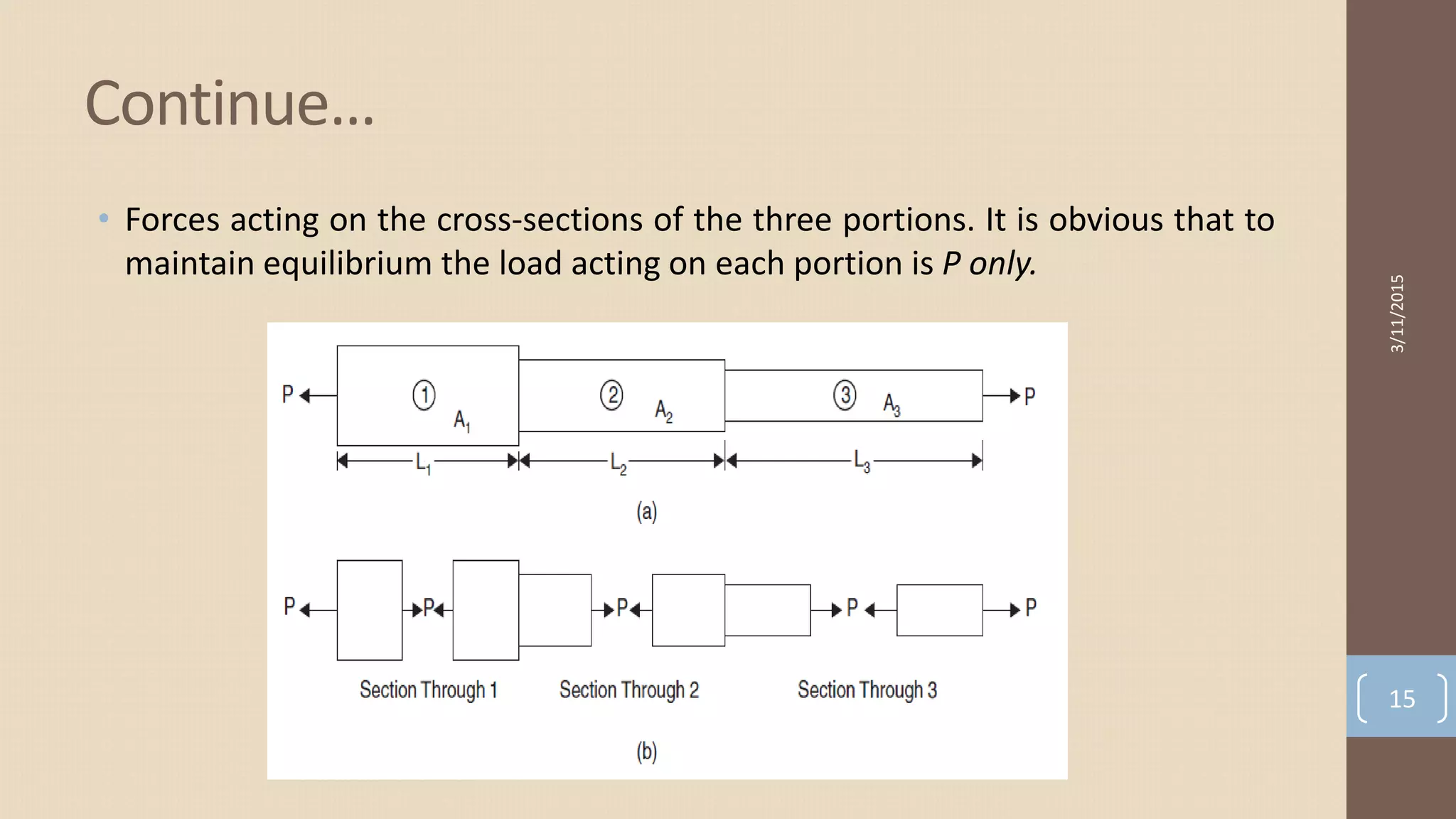
δ = δ1 + δ2 + δ3 = [P L1 / A1 E] + [P L2 / A2 E] + [P L3 / A3 E]
Continue…
3/11/2015
17

18. • Stresses due to Change in Temperature
• Whenever there is some increase or decrease in the temperature of a body, it
causes the body to expand or contract.
• If the body is allowed to expand or contract freely, with the rise or fall of the
temperature, no stresses are induced in the body.
• But, if the deformation of the body is prevented, some stresses are induced in
the body. Such stresses are known as thermal stresses.
Thermal Stresses
3/11/2015
18

19. • l = Original length of the body,
• t = Rise or fall of temperature,
• α = Coefficient of thermal expansion,
∴ Increase or decrease in length,
δl = l × α × t
• If the ends of the body are fixed to rigid supports, so that its expansion is prevented,
then compressive strain induced in the body,
𝜀 𝑐 =
𝛿𝑙
𝑙
=
𝑙 𝛼 𝑡
𝑙
= 𝛼 𝑡
∴ Thermal stress,𝜎𝑡ℎ = 𝜀 𝑐 𝐸 = 𝛼𝑡𝐸
Continue…
3/11/2015
19

20. • Consider a circular bar of diameter d and length l, subjected to a tensile force P
• Due to tensile force, the length
of the bar increases by an amount δl
and the diameter decreases by
an amount δd
• Similarly, if the bar is subjected
to a compressive force,
• Every direct stress is accompanied by a strain in its own direction is known as linear strain
and an opposite kind of strain in every direction, at right angles to it, is known as lateral
strain.
Linear and Lateral Strain
3/11/2015
20

21. • When a body is stressed within elastic limit, the lateral strain bears a constant ratio to the
linear strain.
𝐿𝑎𝑡𝑒𝑟𝑎𝑙 𝑆𝑡𝑟𝑎𝑖𝑛
𝐿𝑖𝑛𝑒𝑎𝑟 𝑆𝑡𝑟𝑎𝑖𝑛
= 𝐶𝑜𝑛𝑠𝑡𝑎𝑛𝑡
• This constant is known as Poisson's ratio and is denoted by (1/m) or μ.
Poisson’s Ratio
3/11/2015
21

22. • When a body is subjected to a system of forces, it undergoes some changes in its dimensions.
The volume of the body is changed.
• The ratio of the change in volume to the original volume is known as volumetric strain.
• Volumetric strain, εv = δV / V ; δV = Change in volume
; V = Original volume.
• Volumetric strain of a rectangular body subjected to an axial force is given as
𝜀 𝑣 =
𝛿𝑣
𝑣
= 𝜀 1 −
2
𝑚
• Volumetric strain of a rectangular body subjected to three mutually perpendicular forces is
given by
εv = εx + εy + εz
Volumetric Strain
3/11/2015
22

23. • When a body is subjected to three mutually perpendicular stresses, of equal intensity, then
the ratio of the direct stress to the corresponding volumetric strain is known as BULK
MODULUS.
• It is usually denoted by K.
• Bulk modulus,
𝐾 =
𝑆𝑡𝑟𝑒𝑠𝑠
𝑉𝑜𝑙𝑢𝑚𝑒𝑡𝑟𝑖𝑐 𝑠𝑡𝑟𝑎𝑖𝑛
=
𝜎
𝛿𝑉
𝑉
Bulk Modulus
3/11/2015
23

24. Thank You
3/11/2015
24