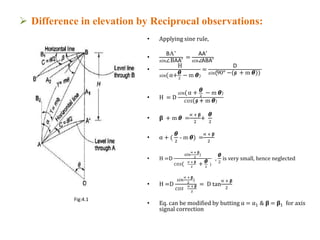
1) The document describes the method of determining the difference in elevation between two stations using reciprocal observations. Observations of vertical angles are made simultaneously from both stations to eliminate the effect of refraction. 2) The mean of the observed vertical angles is used in trigonometric formulas along with the horizontal distance between stations to calculate the difference in elevation. 3) The coefficient of refraction is defined as the ratio of the radius of curvature of the earth to the radius of curvature of the line of sight. A formula is provided to calculate the coefficient of refraction based on the vertical angles observed and the curvature of the earth.

1. Advance Surveying
Trigonometric Leveling
Prof. Rajguru R.S.
Civil Engineering Department
(rajgururajeshcivil@sanjivani.org.in)
Sanjivani College of Engineering,
Kopargaon,MH,India

2. Lecture Outline
Determination of Difference in elevation by
Reciprocal observation
 Introduction
 Equation to determine the difference in
Elevation
 Coefficient of refraction

3.  Determination of Difference in elevation by Reciprocal
observations:
• Introduction:
• In the present method the difference of elevation between two station is
find out, the observation are made simultaneously from both the station to
eliminate the effect of refraction completely. Observations are made in
between 10am to 3pm to minimize the effect of refraction. The mean of
the vertical angle is obtained and used for calculating the difference of
elevation between two station.

4.  Difference in elevation by Reciprocal observations:
• H= Difference in elevation bet. A &B
• ∝ & 𝛃 = Angle observed simultaneously
• D = Horizontal distance = AB
• 𝛾 & C = Angle of refraction & curvature
• ∝1 & 𝛃1 = Corrected vertical angle for axis
signal
• The mean vertical angle =
∝ + 𝛃
2
• ∠B AA’ = [ α + (
ᆈ
2
- m ᆈ) ]
• ∠ ABB’ = [ 𝛃 - (
ᆈ
2
- m ᆈ) ]
• The sign of correction being +ve for angle of
elevation & -ve for angle of depression
• Since the chords AA’ & BB’ are parallel, ∠BAA’
=∠ABB’
• α + (
ᆈ
2
- m ᆈ) = 𝛃 - (
ᆈ
2
- m ᆈ) =
∝ + 𝛃
2
….. .1
Fig.3.1

5.  Difference in elevation by Reciprocal observations:
• Applying sine rule,
•
BA’
𝑠𝑖𝑛∠BAA’
=
AA’
𝑠𝑖𝑛∠ABA’
•
H
𝑠𝑖𝑛(α+ᆈ
2
− m ᆈ)
=
D
𝑠𝑖𝑛(90° −( 𝛃 + m ᆈ))
• H = D
𝑠𝑖𝑛(α + ᆈ
2
− m ᆈ)
𝐶𝑂𝑆( 𝛃 + m ᆈ)
• 𝛃 + m ᆈ =
∝ + 𝛃
2
+
ᆈ
2
• α + (
ᆈ
2
- m ᆈ) =
∝ + 𝛃
2
• H =D
𝑠𝑖𝑛
∝ + 𝛃
2
)
𝐶𝑂𝑆( ∝ + 𝛃
2
+ ᆈ
2
)
,
ᆈ
2
is very small, hence neglected
• H =D
𝑠𝑖𝑛
∝ + 𝛃
2
)
𝐶𝑂𝑆
∝ + 𝛃
2
= D tan
∝ + 𝛃
2
• Eq. can be modified by butting α = α1 & 𝛃 = 𝛃1 for axis
signal correction
Fig:4.1

6.  Coefficient of refraction:
• Coefficient of refraction (m) is the ratio of the radius of curvature of the
earth R to the radius of curvature of the line of sight 𝑅 𝑠
•
• m=
R
𝑅 𝑠
We know C=
ᆈ
2
& 𝛾 = 𝑚ᆈ
• α + (C - 𝛾) = 𝛃 – (C- 𝛾)
• 2𝛾 = α - 𝛃 +2C
• 𝛾 =
1
2
(α - 𝛃 +2C) =
1
2
(α − 𝛃 +2
ᆈ
2
) =
1
2
(ᆈ +α - 𝛃 )
• Butting 𝛾 = 𝑚ᆈ in above eq.
• 𝑚ᆈ =
1
2
(ᆈ +α - 𝛃 )
• 𝑚 =
1
2ᆈ
(ᆈ +α - 𝛃 )

7. Thank you