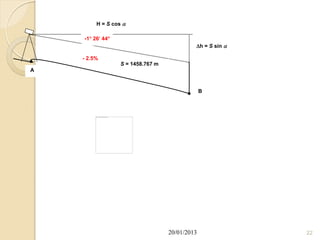
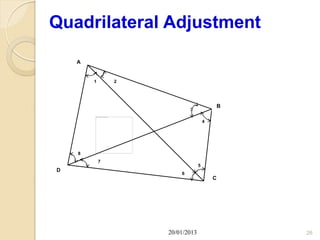
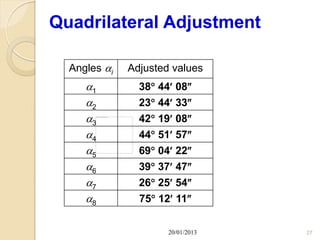
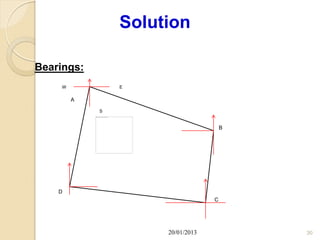
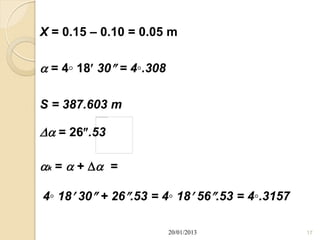Here are the coordinates of points A, B and C: XA = 171,809.49 m YA = YD = 114,056.00 m XB = XA + AB cos (37 28 41) = 171,981.97 m YB = YA + AB sin (37 28 41) = 114,257.39 m XC = XB + BC cos (55 20 14) = 172,053.04 m YC = YB + BC sin (55 20 14) = 113,995.32 m

1. Project Surveying
20/01/2013 1

2. Electronic Distance Measurement
(EDM)
20/01/2013 2

3. • 1950s.
• Large, heavy, complicated and expensive (old EDM).
• Lighter, simpler and less expensive (new EDM).
• EDM Instruments use infrared light, laser light or
microwaves.
• Receiver/Transmitter at one end and Prism at the other end.
• EDM Instruments come in long range (10 – 20) km, medium
range (3 – 10) km and short range (0.5 – 3) km.
• Some laser EDM Instruments measure short distances (100
– 350) m without reflecting prism.
•Microwave instruments are often used in hydrographic
surveys 50 km. Currently GPS.
20/01/2013 3

4. Electronic Angle Measurement
(Total Stations)
Combine the function of Theodolite and EDM
20/01/2013 4

5. Principles of EDM
y
x

 = c/f c = 299,792.458 km/s (in vacuum)
: wavelength (m)
c: velocity (km/s)
f: frequency (Hz, hertz; one cycle per second)
20/01/2013 5

6. Principles of EDM

1
2
3 4
2L = (n + )
 n n-1
c, the velocity of light through the atmosphere can be affected by:
• Temperature
• Atmospheric Pressure
• Water Vapour Content
20/01/2013 6

7. EDM Characteristics
• The more expensive EDM instruments have longer distance range
and higher precision.
Distance Range:
• 800 m – 1 km (single prism).
• Short-range EDM can be extended to 1,300 m using 3 prisms.
• Long-range EDM can be extended to 15 km using 11 prisms.
Accuracy Range:
 (5 mm + 5 ppm) for short-range EDM.
 (2 mm + 1 ppm) for long-range EDM.
20/01/2013 7

8. EDM Characteristics
Measuring Time:
1.5 seconds for short-range EDM.
3.5 seconds for long-range EDM.
Battery Capability:
1,400 – 4200 measurements depending on the size and
condition of battery and the temperature.
Temperature Range:
- 20c + 50c
Non-prism measurements: 100 – 350 m
20/01/2013 8

9. Prisms
Prisms are surveying tools used with EDM and Total Stations to
reflect the transmitted signals.
• Prisms must be tribrach-mounted if a higher level of accuracy is
required (Control Surveys).
• Prisms mounted on adjustable-length prism poles are portable and
suited particularly for (Stakeout and Topographic Surveys)
20/01/2013 9

10. EDM Instrument Accuracies
Accuracy Range:
 (2 mm + 1 ppm) to  (10 mm + 10 ppm)
Constant Instrumental Error e.g. 5 mm represents an accuracy of
1/2,000 at 10 m, 1/20,000 at 100 m, 1/200,000 at 1,000 m.
Measuring error is proportional to the distance being measured
e.g. 10 ppm.
20/01/2013 10

11. Field Method for
Determining the Instrument-Reflector Constant
A B C
AC – AB – BC = Instrument/Present Constant
20/01/2013 11

12. EDM Operation
• Set Up
• Aim
• Measure
• Record
20/01/2013 12

13. Geometry of EDM
• Optical target and reflecting prism
are at the same height
• EDM (S), theodolite ()
• Adjustable-length prism pole
(HR = hi)
• Elev. (B) = Elev. (A) +hi  h - HR
20/01/2013 13

14. Problem 1
Refer to Figure below. A top-mounted EDM instrument
is set up at station A, its elevation, (HA = 650.000 m).
Using the following values, compute the horizontal
distance from A to B and the elevation of B, (HB). The
optical centre of the theodolite is hi = 1.601 m above
station and a vertical angle of + 4◦ 18 30 is measured
to the target, which is 1.915 m (HR) above station B.
The EDM instrument centre is 0.100 m (hi) above the
theodolite and the reflecting prism is 0.150 m (HR)
above the target. The slope distance is measured to
be 387.603 m.
20/01/2013 14

15. Prism
S
HR
Target

EDM 2.065 m
 HR
hi
hi
B
1.701 m
X cos 
S X
A S

k

20/01/2013 15

16. Solution
X cos 
sin  
S
X  HR  hi
20/01/2013 16

17. X = 0.15 – 0.10 = 0.05 m
 = 4◦ 18 30 = 4◦.308
S = 387.603 m
 = 26.53
k =  +   =
4◦ 18 30 + 26.53 = 4◦ 18 56.53 = 4◦.3157
20/01/2013 17

18. Computation of the horizontal distance from A to B (H):
H = S cos (k) = 386.504 m
20/01/2013 18

19. Computation of the elevation of B, (HB):
H B  H A  hi  h  HR
,
20/01/2013 19

20. HA = 650.000 m
h = S sin (k) = 29.168 m
HB = 650.000 + (1.601 + 0.10) + 29.168 – (1.915 + 0.15)
= 678.804 m
HB = 678.804 m
,
20/01/2013 20

21. Problem 2
A line AB is measured at both ends as follows:
At A, slope distance = 1458.777 m,
zenith angle = 91 26 50.
At B, slope distance = 1458.757 m,
zenith angle = 88 33 22.
The heights of the instrument, reflector and target are
equal for each observation.
• Compute the horizontal distance AB.
• If the elevation at A is 590.825 m, what is the
elevation at B?
• Calculate the gradient between A and B.
20/01/2013 21

22. H = S cos 
-1 26 44
h = S sin 
- 2.5%
S = 1458.767 m
A
B
20/01/2013 22

23. Solution
S1 = 1458.777 m, S2 = 1458.757 m
S = (S1 + S2)/2 = 1458.767 m
1 = 90 00 00 - 91 26 50 = - 1 26 50
2 = 90 00 00 - 88 33 22 = 1 26 38
 = (1 + 2)/2 = 1 26 44
20/01/2013 23

24. Solution
H = S cos  = 1458.303 m
HA = 590.825 m,
h = S sin  = 36.800 m.
HB = HA - h = 590.825 - 36.800 = 554.025 m.
Gradient between A and B
= (h/H)  100 = - 2.5%
20/01/2013 24

25. Problem 3
Refer to Figure below; angles 1, 2,…....8 of a
quadrilateral of a triangulation network were
adjusted. If, DA = 213.36 m, XD = 171,719.32 m, YD =
114,056.00 m and the bearing of the line DA is
equal to N 25 00 00 W.
• Calculate the distances AB, BC and CD.
• Calculate the bearings of the lines AB, BC and CD.
• Calculate the coordinates of points A, B and C.
20/01/2013 25

26. Quadrilateral Adjustment
A
1 2
B
3
4
8
7
5
D
6
C
20/01/2013 26

27. Quadrilateral Adjustment
Angles i Adjusted values
1 38 44 08
2 23 44 33
3 42 19 08
4 44 51 57
5 69 04 22
6 39 37 47
7 26 25 54
8 75 12 11
20/01/2013 27

28. Solution
• Distances:
Applying the law of sines by solving triangles:
ABD for AB, ABC for BC, ACD for DC:
AB = AD sin8/sin3 = 306.40 m
BC = AB sin2/sin5 = 132.07 m
CD = AD sin1/sin6 = 209.31 m
20/01/2013 28

29. Solution
Bearings:
If you redraw the figure below, you can calculate
the bearings of the lines AB, BC and CD as follows:
20/01/2013 29

30. Solution
Bearings:
W E
A
S
B
D
C
20/01/2013 30

31. Solution
Bearings:
Brg of AB = (1 + 2) – Brg of AD
= (38 44 08 + 23 44 33) - 25 00 00 = 37 28 41
The complete bearing of line AB is S37 28 41E
Brg of BC = 180 00 00 - (3 + 4 + Brg of BA)
= 179 59 60 - (42 19 08 + 44 51 57 +37 28 41)
= 55 20 14
The complete bearing of line BC is S55 20 14W
Brg of CD = (5 + 6) – Brg of CB
= (69 04 22 + 39 37 47) - 55 20 14 = 53 21 55
The complete bearing of line CD is N53 21 55W
20/01/2013 31

32. Coordinates:
Solution
XD = 171,719.32 m, YD = 114,056.00 m
XA = XD + DA sin (25 00 00) = 171,809.49 m
YA = YD + DA cos (25 00 00) = 114,249.37 m
XB = XA + AB sin (37 28 41) = 171,995.92 m
YB = YA - AB cos (37 28 41) = 114,006.22 m
XC = XB - BC sin (55 20 14) = 171,887.29 m
YC = YB - BC cos (55 20 14) = 113,931.10 m
20/01/2013 32

33. Total Stations
• Background
• Main Characteristics
• Applications
20/01/2013 33

34. Main Characteristics
• Parameter Input
1. Angle Units: degrees or gon.
2. Distance Units: ft or m.
3. Pressure Units: inches HG or mm HG.
4. Temperature Units: F or C.
5. Prism constant (- 0.03 m).
20/01/2013 34

35. Main Characteristics
• Parameter Input
6. Offset distance.
7. Face 1 or face 2 selection.
8. Automatic point no. incrementation.
9. Hi
10. HR
20/01/2013 35

36. Main Characteristics
• Parameter Input
11. Point numbers and code numbers
for occupied and sighted stations.
12. Date and time settings.
20/01/2013 36

37. Main Characteristics
• Capabilities
1. Monitor: battery status, signal attenuation,
horizontal and vertical axes status, collimation
factors.
2. Compute coordinates (N, E, Z).
3. Traverse closure and adjustment, and areas.
4. Topography reductions.
5. Object heights.
6. Distances between remote points.
20/01/2013 37

38. Main Characteristics
• Capabilities
7. Inversing.
8. Resection.
9. Layout (Setting out).
10. Horizontal and vertical collimation corrections.
11. Vertical circle indexing.
12. Records search and review.
13. Loading external programmes.
14. Downloading and uploading.
20/01/2013 38

39. Applications
• Point Location
New Point
B
d2
Reference Control Point
P 
A  Station
20/01/2013 39

40. Applications
• Point Location
• Known:
N, E and Z of A,
N, E and Z of P/Azimuth of AP.
• Measured:
Angles or azimuths from the control point () and d.
• Computed:
N, E and Z of B and azimuth of AB and d.
20/01/2013 40